

umwelt-online: PN 98 - Probenahme aus festen und stichfesten Abfällen sowie abgelagerten Materialien (4)
 |
zurück |  |
| Geräte zur Probenentnahme (in Anlehnung an DIN EN 932-1, Nov. 1996) |
Anhang D |
1. Probenahmegeräte zur Probenentnahme aus ruhenden Abfällen
1.1 Kriterien für Probenahmegeräte
Gemäß Tabelle 3 Kapitel 6.5 erhöht sich das Volumen der Einzelprobe mit zunehmender Stückgut-/Komponentengröße. Die Ausführung der Geräte zur Entnahme von Einzelproben aus ruhenden Abfällen sollte gewährleisten, dass
1.2 Beispiele für Probenahmegeräte
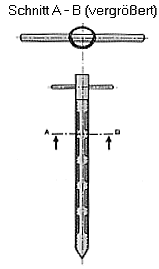
Das Probenahmerohr (vgl. D1) besteht aus zwei ineinander gesteckten Rohren. Beide Rohre haben über ihre Arbeitslänge Öffnungen, so dass, wenn beide Rohre gegeneinander verdreht werden, feinerkörnige Abfallmaterialien in das Probenahmerohr eintreten und dort festgehalten werden.
D1: Probenahmerohr
D2: Probenahmespeer
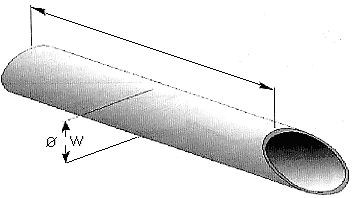
Der Probenahmespeer (vgl. D2) wird insbesondere zur Probenahme feinkörniger Materialien eingesetzt. Er ermöglicht euch die Entnahme von Proben aus dem Inneren von Haufwerken bzw. Big Bags oder Gebinden. Die Länge 1 des Speeres beträgt je nach Einsatzbereich zwischen 1-2 m. Der Innendurchmesser w ist gemäß 1.1 an die Stückgutgröße anzupassen.
2. Mechanische Probenahmegeräte zur Probenentnahme aus bewegten Abfällen
2.1 Kriterien für mechanische Probenahmegeräte
Mechanische Probenahmegeräte werden so ausgeführt, dass bei der Probenahme jede Einzelkomponente des Abfallstromes mit gleicher Wahrscheinlichkeit in die Einzelprobe aufgenommen wird. Die Ausführung des Probenahmegerätes sollte neben den in 1.1 aufgeführten Punkten noch zusätzlich gewährleisten, dass
2.2 Beispiele für Probenahmegeräte:
Bei allen in diesem Abschnitt aufgeführten Probenahmegeräten sind abweichende Ausführungen zulässig, solange die wesentlichen Kriterien für mechanische Probenahmegeräte (vgl. Punkt 1.1) insbesondere zur Weite der Entnahmeöffnung erfüllt und die Geräte zur Durchführung der in Kapitel 9 beschriebenen Probenahmeverfahren geeignet sind. Bei der Probenahme aus bewegten Abfallströmen, z.B. beim Bandabwurf bzw. von laufenden Förderbändern sind festinstallierte Probenahmesysteme heute Stand der Technik und sollten bevorzugt eingesetzt werden.
D3: Probenabstecker (Probenahme von stillgesetzten Fördereinrichtungen)
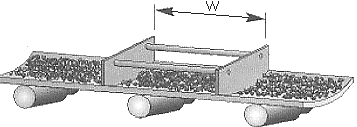
Der Probenahmerahmen (vgl. D3) besteht aus zwei parallelen Blechen. Der Abstand der zwei Bleche sollte etwa die dreifachen Breite des Gutstromes betragen. Die Länge der Bleche entspricht der Breite des Förderbandes. Zur Probenahme wird das Gut zwischen den Abgrenzblechen abgeräumt.
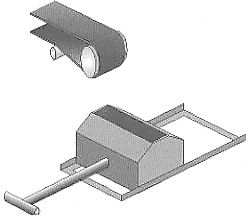
D4: Auffangkasten (Probenahme aus kontinuierlich fallendem Abfallstrom)
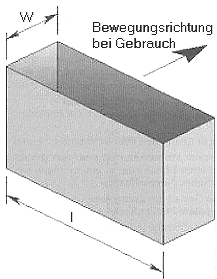
Die oberen Kanten des Auffangkastens (vgl. D4) sind gerundet. Die Weite w der Öffnung ist gem. 2.1 ist so bemessen, dass sie mindestens das dreifache der Stückgutgröße der Größtkomponente beträgt. Die Länge l des Auffangkastens ist mindestens so groß, wie die Breite des Abfallstroms. Die Tiefe des Auffangkastens ist so gewählt, dass kein Probengut durch Herausspringen verloren geht. Aus Gründen der Bedienbarkeit und zur Verbesserung der Reproduzierbarkeit der Probenentnahme wird empfohlen, den Auffangkasten auf einer Führungsschiene durch das Probengut zu bewegen (vgl. D5).
D5: Handbedienter Auffangkasten auf Führungsschiene
Erläuterungen
Die Ausführungen in den Anhängen E, F und G dienen zur inhaltlichen Verdeutlichung dieser Richtlinie und besitzen informativen Charakter
| Problematik zur Repräsentativität der Probenahme | Anhang E (informativ) |
Von grundlegender Bedeutung für die Probenahme ist die Frage, inwieweit entnommene Proben die zu beurteilenden Eigenschaften des Prüfgutes widerspiegeln, somit letztlich als repräsentativ für die Gesamtmenge gelten können.
Als allgemeine Definition einer "repräsentativen Probe" gilt:
| "Probe, deren Eigenschaften weitestgehend den Durchschnittseigenschaften der Gesamtmenge des Prüfgutes entsprechen". |
Homogen sind in der Regel
Heterogen sind alle anderen Abfälle.
Für die Erfüllung der Anforderung nach "repräsentativer Beprobung" heterogener Prüfgüter sind 2 Ansätze denkbar und zwar
Grundlage einer mathematisch-statistisch begründeten Probenahme muss ein Probenahmemodell sein, das Angaben über den Probenahmefehler in Abhängigkeit von der Anzahl der entnommenen Proben, der Probenmenge und der Heterogenität liefert.
Während die Forderung nach " Repräsentativität" bei einer einzelnen Feststoffkomponente sowie bei gasförmigen und flüssigen Phasen noch relativ einfach zu erfüllen ist, ergeben sich bei festen Abfällen mit steigender Heterogenität/Inhomogenität zunehmend Schwierigkeiten.
Die im Zuge der Bearbeitung zu ermittelnden Stoffwerte einer Grundmenge sind primär eine Eigenschaft des Stoffsystems, in zweiter Linie eine Eigenschaft der Probenahme und des Probenahmeortes und zuletzt der Laborarbeiten in Form von Probenauf- und -vorbereitung sowie der Analyse. Berücksichtigt man, dass die eigentliche Bewertung des Stoffsystems auf der Auswertung aller Daten beruht, wird nachvollziehbar, dass vorher Versäumtes in dieser Stufe der Qualitätssicherung nicht mehr revidiert werden kann.
Da der Begriff " Repräsentativität" etwas über die Vertrauenswürdigkeit und Zuverlässigkeit der Stoffbewertung aussagen soll, muss er durch Ansprüche an die dabei möglichen Fehler begründet werden. Um ihn kontrollierbar und vergleichbar zu machen, ist er an Kriterien und Zahlenwerte zu binden.
Bemühungen, solche Kriterien an Forderungen für die Fehler bei der Probenahme, Probenvorbereitung und stofflichen Analyse festzumachen, sind eng mit der Bewertung von körnigen Schüttgütern verbunden. Dort ist festgelegt, wann eine Probenahme oder ein Stoffwert als "exakt", "genau", " systematisch unbeeinflusst", "richtig, " reproduzierbar", " zuverlässig" oder "repräsentativ" gelten kann.
Diese Begriffe werden von verschiedenen Autoren allerdings unterschiedlich interpretiert, so dass bei der Charakterisierung der Repräsentativität Defizite bestehen. Nicht berücksichtigt bei der Zuverlässigkeit der Stoffbestimmung bleiben ökonomische Kriterien wie Kostenabschätzung und Konsequenzen im Falle einer Fehlbewertung.
Im Rahmen dieser Richtlinie wird der gemessene Stoffwert als Summe des wahren Wertes und der zufälligen und/oder auch systematischen Fehler, die bei seiner Bestimmung von der Probenahme bis zur Datenanalyse auftreten können, dargestellt. Die Qualität der Stoffbestimmung wird durch die Eigenschaften dieser Fehler begründet.
So gelten Stoffwerte
| ... | als " genau", |
| wenn die Varianz seiner Fehler eine vorgegebene obere Schranke einhält, | |
| ... | als " systematisch unbeeinflusst", |
| wenn bei seiner Bestimmung kein systematischer Fehler begangen wurde, | |
| ... | als " richtig", |
| wenn der Stoffwert "genau" und "systematisch unbeeinflusst" ist, | |
| ... | als " reproduzierbar", |
| wenn bei Wiederholung der Untersuchung statistisch identische Ergebnisse auftreten | |
| ... | als " exakt", |
| wenn er absolut sicher den wahren Stoffbestand widerspiegelt, was utopisch ist, da Fehler bei der Stoffbestimmung unvermeidlich sind. |
Mit diesen Kriterien sind Aussagen über die Qualität jedes einzelnen Stoffwertes festgelegt. In die Bewertung des gesamten Stoffsystems dagegen werden alle Stoffwerte einbezogen und anhand der gewonnenen Erkenntnisse die konkrete Zielstellung, z.B. Verwertung, Deponierfähigkeit, Grenzwertüberschreitung etc., überprüft. Jede dieser Bewertungen hat Konsequenzen, verursacht Kosten und ist naturgemäß mit einer gewissen Unsicherheit in Form von Folgeschäden belastet.
Drückt man die Konsequenzen, die bei einer fehlerbehafteten Qualitätssicherung erwartet werden müssen, durch Zahlenwerte, z.B. Streuungen von Mittelwerten, Fehlervarianzen von Modellen, Unkosten u. s. w. aus, gelangt man zu dem Begriff des Risikos.
Nimmt man das Risiko als Maßstab wirtschaftlichen Handelns bei der Qualitätssicherung, so sollte ein Datensatz nur akzeptiert werden, wenn ein bestimmtes Risiko, das durch das Bewertungsverfahren und das zugrundegelegte Modell des Stoffsystems festgelegt ist, möglichst klein ist oder einen zulässigen Wert nicht überschreitet.
Ein Datensatz, der diesen Anspruch erfüllt, heißt zuverlässig im Sinne des gewählten Risikos. Unter diesen Festlegungen gilt eine Datenmenge als repräsentativ, wenn sie in ihrer Gesamtheit zuverlässig und jeder einzelne Stoffwert richtig und reproduzierbar ist.
Nachfolgende Abbildung zeigt den schematischen Zusammenhang der einzelnen Kriterien.

Schema der Eigenschaften repräsentativer Stoffdaten
Eine weitere Betrachtung zu Repräsentativitätserwägungen liefert die statistische Beziehung:
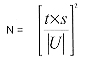
zur Anzahl der zu entnehmenden Einzelproben, wobei die Faktoren folgendes bedeuten:
| N | = | zu entnehmende Anzahl von Einzelproben |
| t | = | Student-Faktor für eine statistische Sicherheit von ca. 95 %, Tabellenwert ca. 2 |
| S | = | Standardabweichung zwischen den Einzelproben hinsichtlich der zu bestimmenden Komponente, in einer Voruntersuchung an mindestens 20 getrennt aufzuarbeitenden Einzelproben zu ermitteln, wobei in gleicher Weise mit gleichen Entnahmemengen vorzugehen ist wie bei der späteren Hauptprobenahme. |
| |U| | = | Genauigkeit, mit der die gesuchte Komponente, bezogen auf das Gesamtmaterial bestimmt werden soll. |
Als Beispiel sei darauf verwiesen, dass bei einer angestrebten Genauigkeit von U = 0,05, einer mittleren Standardabweichung der zu bestimmenden Messgröße von S = 0,27 sich eine notwendige Probenanzahl von etwa 117 Einzelproben ergibt.
Sowohl die Vorgehensweise zur Ermittlung der Standardabweichung als auch die berechnete Anzahl der Einzelproben verdeutlicht, dass eine statistische Betrachtung der Probenahme auf diesem Weg zu unrealistischen Anforderungen führt, die in der Praxis nicht durchführbar sind.
Für die praktische Umsetzung bedeutet dies, dass mit vertretbarem technischen Aufwand im Bereich der Abfallprobenahme keine repräsentative Beprobung im wissenschaftlich-statistischen Sinne möglich ist.
Der zweite Ansatz setzt die genaue Kenntnis der Abfallzusammensetzung in Art, Menge sowie in ihrer räumlichen und zeitlichen Verteilung innerhalb der Grundmenge voraus, so dass gewährleistet ist, dass sämtliche Einzelchargen
proportional erfasst und zu Durchschnittsproben zusammengeführt werden.
Dies impliziert, dass in Fällen unbekannter Zusammensetzung, Verteilung und mangelnder Unterscheidbarkeit keine anteilige Erfassung der Einzelchargen möglich und somit der Anspruch auf "Repräsentativität" nicht erfüllbar ist.
Sammelproben, über die gesamte Grundmenge entnommen, würden hier zu willkürlichen Mengenverhältnissen ohne Bezug zur Grundgesamtheit führen und somit zu nicht reproduzierbaren Zufallsergebnissen ohne Aussagekraft.
Es bleibt festzustellen, dass eine "repräsentative Probenahme" bei heterogenen, festen Abfällen i. d. R. mit vertretbarem Aufwand nicht möglich ist. Daher sollte hier allgemein von abfallcharakterisierenden Proben bzw. von einer abfallcharakterisierenden Probenahme gesprochen werden.
| Bestimmung der Streuung bei der Probenahme | Anhang F (informativ) |
Durch Mehrfachprobenahme in Anlehnung an DIN EN 932-1
1. Einführung
Mit dem folgenden Verfahren kann geprüft werden, ob die Anzahl k der Einzelproben, aus denen eine Sammelprobe gebildet wird, für das verwendete Prüfverfahren ausreichend ist. Das Verfahren ermöglicht die Bestimmung der Standardabweichung des Probenahmeverfahrens und deren Vergleich mit der Wiederholstandardabweichung eines Prüfverfahrens.
Falls die Standardabweichung des Probenahmeverfahrens größer ist als des Wiederholstandardabweichung, dann sollte die Anzahl der Einzelproben von k auf k' erhöht werden (siehe 4.).
2. Durchführung
Unter Verwendung des zu untersuchenden Probenahmeverfahrens werden zu mindestens 15 Zeitpunkten jeweils zwei Sammelproben als Parallelproben entnommen. Jede Sammelprobe wird zu einer Laboratoriumsprobe vorbereitet; dann werden aus jeder Laboratoriumsprobe zwei Analysenproben hergestellt. Mit dem für diese Bestimmung ausgewählten Prüfverfahren wird für jede Analysenprobe ein Prüfergebnis ermittelt. Die Zeitpunkte der Probenahme können über einen größeren Zeitraum verteilt werden.
3. Berechnungen
Die folgenden Gleichungen sind nur für Parallelproben gültig; n ist die Anzahl der Zeitpunkte, zu denen parallele Sammelproben entnommen werden. Die Zeitpunkte seien mit i = 1,2, ..., n bezeichnet,
Die zwei zum gleichen Zeitpunkt entnommenen Sammelproben werden jeweils durch die Symbole a und B unterschieden.
Es bedeuten:
mAi Mittel der zwei Prüfergebnisse a zum Zeitpunkt
mBi Mittel der zwei Prüfergebnisse B zum Zeitpunkt
dAi Differenz zwischen den zwei Prüfergebnissen für Probe a zum Zeitpunkt
dBi Differenz zwischen den zwei Prüfergebnissen für Probe B zum Zeitpunkt Man berechnet die folgenden Größen:
Gesamtmittel:
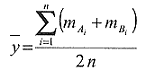
Varianz innerhalb der Proben:
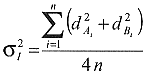
Varianz zwischen den Proben:
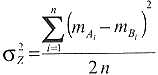
Wiederholstandardabweichung:
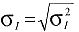
Standardabweichung des Probenahmeverfahrens:
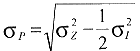
4. Anpassung der Zahl der Einzelproben
Falls σp > σl ist, wird die Anzahl der Einzelproben erhöht, aus denen Sammelproben für das Prüfverfahren, dass zur Beurteilung benutzt wird, gebildet werden. Eine geeignete Anzahl k der Einzelproben kann anhand der folgenden Gleichung geschätzt werden:
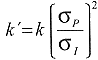
Hierin bedeuten:
k' erforderliche Anzahl der Einzelproben,
k Anzahl der Einzelproben, die in B.2 je Sammelprobe genommen wurden,
σl Wiederholstandardabweichung
σp Standardabweichung des Probenahmeverfahrens
| Bestimmung der Mindestanzahl von Einzelproben je Mischprobe und der Mindestanzahl von Mischproben je Prüfgut | Anhang G (informativ) |
1. Motivation
Abfälle und abgelagerte Stoffgemische sind in der Regel schlecht durchmischt. Je schlechter die Durchmischung ist, umso mehr Proben sind für eine verlässliche Bewertung zu entnehmen. Dabei kann man schnell an wirtschaftliche Grenzen gelangen. Um Analysenkosten einzusparen, werden deshalb mehrere Einzelproben zu einer Mischprobe vereinigt und gemischt. Aus der Mischprobe werden die Proben für die Analyse hergestellt. Entnimmt man die Einzelproben gleichmäßig über das Haufwerk verteilt und hält man sich dabei in Bezug auf die Anzahl der Einzelproben je Mischprobe und die Anzahl der Mischproben je Haufwerk an gewisse Regeln, ist es möglich, "repräsentative" und nachvollziehbare Messergebnisse zu erhalten. Im Folgenden werden solche Regeln mit einem statistischen Modell begründet.
2. Statistisches Modell
2.1 Allgemeines
In einem Haufwerk mit zufälliger Struktur geben die statistischen Methoden der Bewertung davon aus, dass die statistischen Gesetzmäßigkeiten des Merkmals, ausgedrückt durch dessen Verteilungsfunktion mit ihren Parametern wie z.B. Erwartungswert und Varianz, im gesamten Haufwerk nicht von der Ortslage der Probe abhängen. Der Erwartungswert wird durch den Mittelwert und die Varianz wird durch die Streuung der Einzelproben beurteilt.
In größeren Abfallhaufwerken und -stoffströmen kann sich der Stoffbestand auch gerichtet oder geschichtet verändern. Für ihre Bewertung werden besondere statistische Modelle verwendet, die den Ort oder den Zeitpunkt der Probenahme berücksichtigen.
Wenn das Ziel der Untersuchung nur darin besteht, Mittelwert und Streuung zu berechnen, muss man für eine bestimmte Stoffgruppe, Anlieferungsform,
Lagerungsart u. a zunächst die Größe des Haufwerkes (Volumen oder Masse) festlegen, in der noch eine rein zufällige Struktur angenommen werden kann Diese Größe stellt die Mindestgröße für ein Haufwerk dar, für die statistische Gesetzmäßigkeiten ermittelt werden sollten. Sie heißt die Basisgröße (Basismenge) V0 und entspricht der " Grundgesamtheit" im Sprachgebrauch der mathematischen Statistik. Größere Haufwerke V1, auf die diese Gesetzmäßigkeiten übertragen werden können, werden dann als ein Vielfaches der Basismenge aufgefasst.
Um den Aufwand für die Untersuchung zu begrenzen, werden aus mehreren Einzelproben Mischproben gebildet. Grundsätzlich müssen umso mehr Einzelproben für eine Mischprobe entnommen werden
Hat man die Anzahl der Einzelproben für eine Mischprobe für eine Basismenge V0 bestimmt, ergibt sich als ein Vielfaches davon die Probenanzahl für ein aktuelles, größeres Haufwerk V1. Der Proportionalitätsfaktor soll durch die Forderung bestimmt werden, dass die Streuung des Mittelwertes aus den Einzelproben im aktuellen Haufwerk V1 gleich der Streuung des Mittelwertes aus den Einzelproben in der Basismenge V0 ist. Ist diese Forderung erfüllt, hat man das Recht, die Einzelproben, ohne sie zu analysieren, zu einer Mischprobe zu vereinigen und an ihrer Stelle nur den Analysenwert der Mischprobe zu verwenden. Dieser Wert ist dann genauso zuverlässig wie wenn man die Einzelproben jede für sich analysiert und daraus den Mittelwert berechnet hätte.
Nach den gleichen Überlegungen ist dann die Anzahl der Mischproben fest zulegen, die für ein Haufwerk analysiert werden. Es scheint vernünftig, so viele Mischproben zu analysieren, dass der Mittelwert daraus nicht weniger zuverlässig ist als der einzelne Wert aus der Mischprobe. Die Anzahl der Mischproben je Haufwerk müsste dann auf derselben Basis festgelegt werden wie die Anzahl der Einzelproben je Mischprobe.
Im konkreten Fall muss zunächst die Basismenge V0 für eine Stoffgruppe ermittelt werden. Anschließend sind die folgenden Schritte umzusetzen:
Die Angaben sind in jedem Falle als Mindestanzahlen zu behandeln, da sie auf Mindestanforderungen beruhen.
2.2 Anzahl der Einzelproben je Mischprobe für eine Basisgröße V0
Wir bezeichnen mit Y0 die interessierende Messgröße in einem Haufwerk der Basisgröße V0. Y0 ist eine normalverteilte Zufallsgröße mit dem Erwartungswert µ und der Standardabweichung σY0. Ist die Messgröße z.B. der Gehalt eines Merkmals, entspricht der Erwartungswert dem wahren Gehalt, und die Standardabweichung σY0 gibt die mittlere Abweichung eines Einzelwertes vom wahren Gehalt an. Wird der Einzelwert durch Proben bestimmt, enthält die Standardabweichung sowohl die natürliche, dem Abfallhaufwerk innewohnende Variabilität als auch die Unsicherheit durch die Probenahme. Der wahre Gehalt p ist nicht bekannt und muss durch den Mittelwert L aus einer endlichen Anzahl von n Proben beurteilt werden. Der Mittelwert entspricht in der Regel nicht dem wahren Wert. Fr weicht von diesem um einen zufälligen Betrag ab. Diese Abweichung besitzt eine bestimmte Wahrscheinlichkeitsverteilung.
Fordert man z.B., dass der Mittelwert bei einem gewählten β höchstens um den Betrag ε0 vom wahren Wert abweicht, d. h.
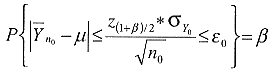 ( 1)
( 1)
gilt, ergibt sich die Anzahl der dafür erforderlichen Einzelproben n0:
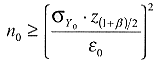 ( 2)
( 2)
Der Wert ε0 heißt die zulässige Abweichung des Mittelwertes bei der gewählten Vertrauenswahrscheinlichkeit.
Wählt man wie technisch üblich eine Vertrauenswahrscheinlichkeit von 95 % und rundet man den z-Wert z(1+0,95)/2 = z0,975 = 1,96 auf "2", ergibt sich die vereinfachte Abschätzung:
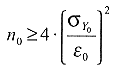 ( 3)
( 3)
Soll weiterhin der Mittelwert so genau sein wie der Einzelwert, d.h. e0 = σY0, mindestens
n0 ≥ 4 ( 3a)
Proben zu vereinigen. In manchen Fällen werden noch 1 bis 2 Proben dazugenommen, wenn man sicher gehen will, dass der Mischprobenwert nicht durch Ausreißer verzerrt wird.
Soll der Mittelwert nur halb so ungenau sein wie der Einzelwert, d. h. e0 = σY0/2, sind bereits mindestens
n0= 16 ( 3b)
Einzelproben zu untersuchen.
2.3 Anzahl der Einzelproben je Mischprobe für ein aktuelles Haufwerk der Größe V1
Der Proportionalitätsfaktor für die Umrechnung der Mindestprobenanzahl einer Mischprobe aus der Basisgröße in die Größe eines aktuellen Haufwerkes beruht auf dem folgenden statistischen Modell.
Y0 ist die Messgröße im Haufwerk der BasisgrößeV0, und Y1 ist die Messgröße im aktuellen Hautwerk der Größe V1. Die entsprechenden Streuungen (mittleren quadratischen Abweichungen der Einzelwerte vom Erwartungswert) seien e0 = σY02 und σY12. Dann sind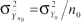 die Streuung des Mittelwertes (mittlere quadratische Abweichung des Mittelwertes vom Erwartungswert) aus n0 Einzelproben in der Basisgröße V0 und
die Streuung des Mittelwertes (mittlere quadratische Abweichung des Mittelwertes vom Erwartungswert) aus n0 Einzelproben in der Basisgröße V0 und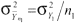 die Streuung des Mittelwertes aus n1 Einzelproben im aktuellen Haufwerk der Größe V1. Aus der Forderung, dass die Streuungen der Mittelwerte aus der Basismenge und der aktuellen Haufwerkmenge gleich sein sollen, könnte nun die Mindestanzahl der Einzelproben n1 berechnet werden:
die Streuung des Mittelwertes aus n1 Einzelproben im aktuellen Haufwerk der Größe V1. Aus der Forderung, dass die Streuungen der Mittelwerte aus der Basismenge und der aktuellen Haufwerkmenge gleich sein sollen, könnte nun die Mindestanzahl der Einzelproben n1 berechnet werden:
 ( 4)
( 4)
Da die Einzelproben nicht untersucht werden, sind die Streuungen der Messgrößen in der Regel nicht bekannt. Leicht abzuschätzen sind aber die Größen der zu untersuchenden Haufwerke, entweder das Volumen oder bei bekannter Schüttdichte die Masse.
Aus der Bewertung bergbaulicher mineralischer Massengüter ist bekannt, dass die Streuung einer Messgröße in einem Haufwerk proportional dem Logarithmus der Größe des Haufwerkes ist. Für die Beziehung in (4) gilt damit näherungsweise die Abschätzung mit einer geeignet gewählten positiven Zahl p
 ( 5)
( 5)
Mit der gewöhnlichen Quadratwurzel (p = 2) liegt man insbesondere mit zunehmendem Verhältnis der Haufwerkgrößen V1/V0 deutlich auf der sicheren Seite.
Diese Regel sichert, dass der Mischprobenwert aus dem größeren Haufwerk genauso vertrauenswürdig ist wie der aus der Basismenge.
2.4 Anzahl der Mischproben für eine Basisgröße des Haufwerkes
Damit für die Bewertung des Haufwerkes anhand des Mittelwertes aus den Mischprobenanalysen keine Informationen verschenkt werden, ist es erforderlich, die Anzahl der Mischproben so festzulegen, dass der Mittelwert aus allen Mischproben nicht unzuverlässiger ist als jeder einzelne Mischprobenwert.
Wir bezeichnen mit Yi* den Messwert der i-ten Mischprobe in einem beliebigen Haufwerk. Dieser Messwert ist aufzufassen als Mittelwert aus allen n0 Einzelproben, die zu der Mischprobe vereinigt werden. Bezeichnet man mit Yij den Messwert der j-ten Einzelprobe für die i-te Mischprobe, falls diese Einzelprobe analysiert worden wäre, und geht man davon aus, dass in dem Messwert auch die Messunsicherheiten durch Probenvorbereitung und Analyse enthalten sind, ist der Messwert der i-ten Mischprobe gleich dem Mittelwert aus allen Einzelprobenwerten:
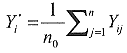 ( 6)
( 6)
Es muss vorausgesetzt werden, dass die Einzelproben zu gleichen Teilen zur Mischprobe vereinigt werden und dass das gesamte Probenmaterial homogenisiert wird.
Ist σY02 die Streuung des Messwertes der Einzelprobe, ergibt sich die Streuung des Mischprobenwertes als Streuung des Mittelwertes der zugrundegelegten Einzelproben:
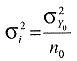 ( 7)
( 7)
Entnimmt man m Mischproben, hat der Mittelwert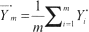 daraus die Streuung
daraus die Streuung
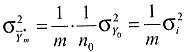 ( 8)
( 8)
Die Quadratwurzel hieraus ist die Standardabweichung des Mischprobenmittelwertes.
Mit Hilfe der Standardabweichung für den Mischprobenmittelwert kann nun nach den gleichen Überlegungen wie bei der Bestimmung der Einzelprobenanzahl je Mischprobe die notwendige Mindestanzahl an Mischproben m0 abgeschätzt werden. Es wird gefordert, dass der Mittelwert xxxxxxxx, um nicht mehr als ein ε0* mit der Vertrauenswahrscheinlichkeit β vom wahren bzw. erwarteten Gehalt µ des Haufwerkes abweichen soll.
Eine sinnvolle Forderung wäre z.B., dass der Mittelwert aus allen Mischproben mindestens genauso verlässlich ist wie der einzelne Mischprobenwert bzw. wie der Mittelwert der ihm zugrundegelegten Einzelproben. Ersetzt man in der 1 Beziehung ( 1) den Mittelwert aus n0 Einzelproben Yn0, durch den Mittelwert aus m0 Mischproben Y'm0 die Standardabweichung des Einzelprobenmittelwertes durch die des Mischprobenmittelwertes
durch die des Mischprobenmittelwertes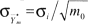 , die zulässige Abweichung ε0 durch die neue Schranke ε0* sowie n0 durch m0, ergibt sich die zu ( 2) analoge Abschätzung für die notwendige Mindestanzahl an Mischproben:
, die zulässige Abweichung ε0 durch die neue Schranke ε0* sowie n0 durch m0, ergibt sich die zu ( 2) analoge Abschätzung für die notwendige Mindestanzahl an Mischproben:
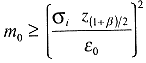 ( 9)
( 9)
Ersetzt man hierin a, durch den Ausdruck in (7), ergibt sich
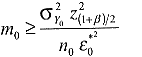 ( 10)
( 10)
Fordert man, dass der Mittelwert aus den Mischproben genauso gut ist wie eine Einzelprobe (ε0* = σY0) und beruht der Mischprobenwert auf n0 = 4 Einzelproben, ist bei einer Vertrauenswahrscheinlichkeit von 95 % (Rundung des z-Wertes auf 2) mindestens
m0 ≥ 1 ( 10a)
Mischprobe zu bilden.
Wenn die Einzelproben mehr oder weniger regelmäßig über das Prüfgut verteilt werden, werden ausgesprochene Ausreißer von Mischproben selten sein. Um sicher zu gehen, sollten dennoch wenigstens m0 = 2 Mischproben gebildet werden.
Bei höheren Genauigkeitsansprüchen sind entsprechend mehr Mischproben für die Basismenge zu untersuchen.
2.5 Anzahl der Mischproben für ein aktuelles Haufwerk
Mit der Größe des Haufwerkes nimmt die Möglichkeit zu, dass die räumliche Variabilität nicht mehr rein zufällig ist, sondern dass sich gerichtete Veränderungen oder stückweise homogene Bereiche und Abschnitte in einem Abfallhaufwerk oder Abfallstrom herausbilden, z.B. durch bestimmte Strategien der Anlieferung und Verkippung, durch technologische Regelungen beim Abfallmanagement usw. Ein größeres und schlechter durchmischtes Haufwerk muss durch mehr Mischproben belegt werden als eine entsprechende, kleinere Basismenge.
Ein Proportionalitätsfaktor dafür nach denselben Regeln bestimmt wie bei der Vervielfachung der Einzelprobenanzahl je Mischprobe. Gefordert wird nun, dass die Streuung des Mittelwertes aus allen Mischproben im aktuellen Haufwerk gleich der Streuung des entsprechenden Mittelwertes in der Basismenge ist.
Es darf davon ausgegangen werden, dass das Haufwerk sehr viel, mindestens jedoch um das 10-fache, größer ist als die Mischprobe. Legt man die Basisgröße V0 und die aktuelle Haufwerkgröße V1 zugrunde, ergibt sich analog zu der Abschätzung ( 5) die aktuelle Mischprobenanzahl durch
 ( 11)
( 11)
Mit p = 2 liegt man auf der sicheren Seite. In begründeten Fällen kann auch ein anderer Proportionalitätsfaktor gewählt werden. Gegebenenfalls ist auch mit zunehmender Haufwerkgröße die Basismenge neu festzulegen.
1) vgl. Handbuch Altlasten der HLUG, Bd. 7, Teil 4
 |
ENDE |  |
(Stand: 08.09.2025)
Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: ab 105.- € netto (Grundlizenz)
(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)
Die Zugangskennung wird kurzfristig übermittelt
? Fragen ?
Abonnentenzugang/Volltextversion