umwelt-online-Demo: Archivdatei - KTA 3201.2 - Komponenten des Primärkreises von Leichtwasserreaktoren (3)

a 4 Rohrleitungen

a 4.1 Allgemeines

(1) Die nachstehenden Berechnungsregeln gelten für die Dimensionierung einzelner Rohrleitungsbauteile bei Belastung durch inneren Überdruck, dessen Höhe sich aus dem Auslegungsdruck ergibt. Zusatzbelastungen, zum Beispiel äußere Kräfte und Momente sind gesondert zu erfassen und zu berücksichtigen, wobei für Rohrleitungsbauteile die in Abschnitt 8.4 enthaltenen Regelungen herangezogen werden können.

(2) Wird im Rahmen der Dimensionierung eine Nachrechnung von den mit der Nennwanddicke s_nausgeführten Bauteilen durchgeführt, so ist innerhalb dieses Anhangs a 4 mit der Wanddicke s_0n= s_n- c₁- c₂zu rechnen.

(3) Die Bilder dieses Anhangs berücksichtigen nicht die Zuschläge.

a 4.2 Zylinderschalen unter innerem Überdruck

Die Berechnung erfolgt nach Abschnitt a 2.2.2.

a 4.3 Rohrbogen und Rohrbiegungen unter innerem Überdruck

a 4.3.1 Geltungsbereich

Die nachstehende Berechnung gilt für Bogen und Biegungen unter innerem Überdruck, bei denen das Verhältnis d_a / d_i≤ 1,7 ist. Durchmesserverhältnisse d_a / d_i≤ 2 sind zulässig, wenn die Wanddicke s_0nd 80 mm ist.

A.4.3.2 Berechnungsgrößen und Einheiten zu Abschnitt a 4

Formelzeichen	Berechnungsgröße	Einheit
d_m	mittlerer Durchmesser (siehe Bild a 4-1)	mm
d_i	innerer Durchmesser	mm
d_a	äußerer Durchmesser	mm
r, R	Biegeradien (siehe Bild a 4-2)	mm
s_0i	rechnerisch erforderliche Wanddicke der Bogeninnenseite	mm
s_0a	rechnerisch erforderliche Wanddicke der Bogenaußenseite	mm
B_i	Berechnungsbeiwert zur Ermittlung der Wanddicke der Bogeninnenseite	-
B_a	Berechnungsbeiwert zur Ermittlung der Wanddicke der Bogenaußenseite	-
σ_i	mittlere Spannung an der Bogeninnenseite	N / mm²
σ_a	mittlere Spannung an der Bogenaußenseite	N / mm²
h_m	Faltenhöhe	mm
a	Abstand zweier benachbarter Falten	mm

Bild a 4-1: Falten am Rohrbogen

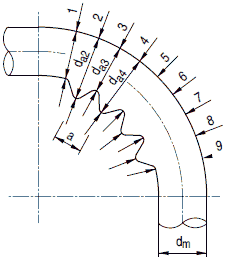
Hinweis:
Die Falten in Bild a 4-1 sind der Deutlichkeit wegen überhöht dargestellt.

Bild a 4-2: Bezeichnungen am Rohrbogen s

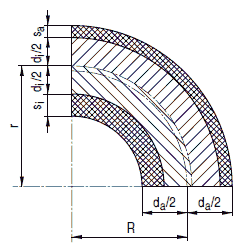
a 4.3.3 Zulässige Faltenbildung

Falten, die in ihren Abmessungen die folgenden Bedingungen erfüllen, bedürfen keiner rechnerischen Nachprüfung:

a) Faltenhöhe

	d_a2+ d_a4
h_m =		- d_a3≤0,03 ⋅ d_m
	2

(a 4-1)

b) Verhältnis Faltenabstand a zu Faltenhöhe hm

a / h_m ≥ 12

(a 4-2)

a 4.3.4 Berechnung

(1) Für die Wanddickenberechnung des Bogens oder der Biegung unter innerem Überdruck gelten die Anforderungen des Abschnitts a 2.2.2, wobei zu berücksichtigen ist, dass die Beanspruchung an der Innenseite um den Berechnungsbeiwert B_i größer und an der Außenseite um B_akleiner ist als bei den geraden Zylinderschalen.

(2) Die rechnerisch erforderliche Wanddicke an der Bogeninnenseite ergibt sich aus:

s_0i = s₀ ⋅ B_i

(a 4-3)

(3) Die rechnerisch erforderliche Wanddicke an der Bogenaußenseite ergibt sich aus:

s_0a = s₀⋅ B_a

(a 4-4)

(4) Ermittlung des Berechnungsbeiwerts B_i

Für Bogen und Biegung mit vorgegebenem Innendurchmesser gilt:

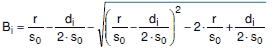(a 4-5)

Der Berechnungsbeiwert B_idarf auch in Abhängigkeit von r/d_iund s₀/d_iaus Bild a 4-3 entnommen werden.

Für Bogen und Biegung mit vorgegebenem Außendurchmesser gilt:

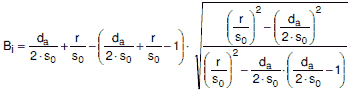(a 4-6)

Der Berechnungsbeiwert Bi darf auch in Abhängigkeit von R/da und s₀/d_aaus Bild a 4-4 entnommen werden.

(5) Ermittlung des Berechnungsbeiwertes B_a

Für Bogen und Biegung mit vorgegebenem Innendurchmesser gilt:

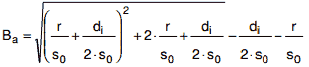(a 4-7)

Der Berechnungsbeiwert B_a darf in Abhängigkeit von r/d_iund s₀/d_iaus Bild a 4-5 entnommen werden.

Für Bogen und Biegung mit vorgegebenem Außendurchmesser gilt:

(a 4-8)

Der Berechnungsbeiwert B_akann in Abhängigkeit von R/d_aund s₀/d_aaus Bild a 4-6 entnommen werden.

(6) Berechnung der Spannungen

In den Gleichungen (a 4-9) bis (a 4-12) sind entweder die Nenndurchmesser d_anund d_inin Verbindung mit den Wanddicken s_0naund s_0nioder ausgeführte Durchmesser in Verbindung mit ausgeführten Wanddicken abzüglich der Zuschläge c₁und c₂zu verwenden.

Die Festigkeitsbedingung für die Bogeninnenseite bei vorgegebenem Innendurchmesser lautet:

	p ⋅ sd_i		2 ⋅ r - 0,5 ⋅ d_i		p
`σ_i =		⋅		+		≤ S_m
	2 ⋅ s_0i		2 ⋅ r - d_i- s_0i		2

(a 4-9)

Die Festigkeitsbedingung für die Bogeninnenseite bei vorgegebenem Außendurchmesser lautet:

	p ⋅ (d_a- s_0i- s_0a)		2 ⋅ R - 0,5 ⋅ d_a + 1,5 ⋅ s_0i- 0,5 ⋅ s_0a		p
`σ_i =		⋅		+		≤ S_m
	2 ⋅ s_0i		2 ⋅ R - d_a + s_0i		2

(a 4-10)

Die Festigkeitsbedingung für die Bogenaußenseite bei vorgegebenem Innendurchmesser lautet:

	p ⋅ d_i		2 ⋅ r + 0,5 ⋅ d_i		p
`σ_a =		⋅		+		≤ S_m
	2 ⋅ s_0a		2 ⋅ r + d_i - s_0a		2

(a 4-11)

Die Festigkeitsbedingung für die Bogenaußenseite bei vorgegebenem Außendurchmesser lautet:

	p ⋅ (d_a- s_0i- s_0a)		2 ⋅ R + 0,5 ⋅ d_a + 1,5 ⋅ s_0i- 1,5 ⋅s_0a		p
`σ_a =		⋅		+		≤ S_m
	2 ⋅ s_0a		2 ⋅ R + d_a + s_0a		2

(a 4-12)

a 4.4 Rohrbogen und Rohrbiegungen unter äußerem Überdruck

Für Bogen und Biegungen unter äußerem Überdruck gelten alle in Abschnitt a 2.2 angeführten Bedingungen mit folgenden Zusätzen:

a) Die Beullänge l ist über die gestreckte Länge des Bogens oder der Biegung zu ermitteln.

b) Bei der Berechnung gegen plastisches Verformen nach Abschnitt a 2 ist der zusätzliche Sicherheitsbeiwert f_v = 1,2 durch f_vB nach folgender Gleichung zu ersetzen:

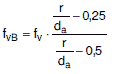(a 4-13)

Bild a 4-3: Berechnungsbeiwert Bi für die Bogeninnenseite bei vorgegebenem Innendurchmesser

Bild a 4-4: Berechnungsbeiwert Bi für die Bogeninnenseite bei vorgegebenem Außendurchmesser

Bild a 4-5: Berechnungsbeiwert Ba für die Bogenaußenseite bei vorgegebenem Innendurchmesser

Bild a 4-6: Berechnungsbeiwert Ba für die Bogenaußenseite bei vorgegebenem Außendurchmesser

a 4.5 Reduzierstücke

Die Berechnung erfolgt nach den Festlegungen des Abschnittes a 2.4.2.

a 4.6 Einschweiß-T-Stücke

a 4.6.1 Aus dem Vollen geschmiedete Einschweiß-T-Stücke

a 4.6.1.1 Geltungsbereich

(1) Diese Berechnungsregeln gelten für aus dem Vollen geschmiedete, gebohrte und gedrehte Einschweiß-T-Stücke kleiner als oder gleich DN 100. Sie berücksichtigen nur die durch Innendruck hervorgerufenen Beanspruchungen. Zusätzliche Kräfte und Momente müssen gesondert berücksichtigt werden.

(2) Die Maße a und b (siehe Bild a 4-7) dürfen die in DIN EN 10253-2 und DIN EN 10253-4 angegebenen Werte für F und G nicht unterschreiten.

Bild a 4-7: Abzweigstück aus dem Vollen geschmiedet, gebohrt und gedreht

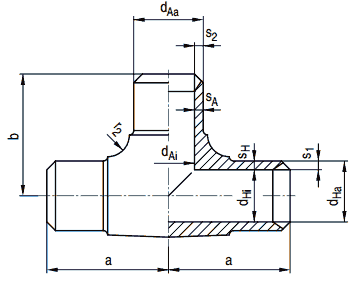
(3) Der äußere Rundungsradius r₂ muss mindestens 0,1 ⋅ d_Aabetragen.

(4) Ein Wanddickenverhältnis s_A/s_H ist bis maximal 2 zulässig für d_Aikleiner als oder gleich 50 mm. Dies gilt auch für Abzweige mit d_Aigrößer als 50 mm, sofern das Durchmesserverhältnis d_Ai/d_Hikleiner als oder gleich 0,2 ist. Bei Abzweigen mit einem Durchmesserverhältnis d_Ai/d_Higrößer als 0,2 soll s_A/s_Hgrundsätzlich den Wert 1,3 nicht überschreiten. Größere Werte sind erlaubt, wenn

die über vorgenanntes Wanddickenverhältnis hinausgehende zusätzliche Wanddicke des Stutzens nicht zur Verstärkung des Stutzenausschnittes herangezogen, sondern aus konstruktiven Gründen gewählt wird oder
der Stutzen mit verkürztem Verstärkungsbereich ausgeführt wird (z.B. Stutzen, die aus Gründen der verbesserten Prüfbarkeit des Rohrleitungsanschlusses konisch ausgebildet sind), wobei die durch die verkürzte Einflusslänge fehlende Verstärkungsfläche im verkürzten Einflussbereich zusätzlich untergebracht werden darf oder
das Verhältnis von Stutzendurchmesser zum Durchmesser des Grundkörpers kleiner als oder gleich 1 : 10 ist.

a 4.6.1.2 Allgemeines

Die Verschwächung des Grundkörpers darf durch Wanddickenvergrößerung der hoch beanspruchten Zone im Ausschnittbereich (siehe Bild a 4-7), wie es durch Schmieden und spanabhebende Bearbeitung erfolgen kann, ausgeglichen werden.

a 4.6.1.3 Berechnungsgrößen und Einheiten

Berechnungsgrößen und Einheiten siehe Abschnitt a 4.7.3 und Bild a 4-7. Zusätzlich gilt:

Formelzeichen	Berechnungsgröße	Einheit
d_Ha	Außennenndurchmesser für Durchgangsanschluss	mm
d_Aa	Außennenndurchmesser für Abzweiganschluss	mm
s₁	Nennwanddicke für Durchgangsanschluss	mm
s₂	Nennwanddicke für Abzweiganschluss	mm
s_A⁺	Äquivalente Wanddicke für Abzweiganschluss	mm
s_H⁺	Äquivalente Wanddicke für Durchgangsanschluss	mm
p⁺	zulässiger Innendruck des T-Stückes	MPa

a 4.6.1.4 Berechnung

(1) Für die Berechnung der mittragenden Längen des Grundkörpers und des Abzweiges gilt der Abschnitt a 4.7.4.2.

(2) Die Ermittlung der erforderlichen Verstärkungsfläche muss nach Abschnitt a 4.7.4.1 erfolgen.

a 4.6.1.5 Äquivalente Anschlusswanddicken

Die für die Spannungsanalyse nach Abschnitt 8.4 benötigten äquivalenten Anschlusswanddicken s⁺_Hund s⁺_asind als diejenigen Wanddicken definiert, die sich für Rohre mit den Außendurchmessern d_Haund d_Aaergeben, wenn sie mit dem für das T-Stück als zulässig ermittelten Innendruck p₊ dimensioniert werden. Es gilt demnach:

	p⁺ ⋅ d_Ha
s_H⁺=
	2 ⋅ S_m+ p

(a 4-14)

s_A⁺= s⁺_H⁺_⋅ d_Aa/ d_Ha

(a 4-15)

Vereinfachend kann p⁺ = p gesetzt werden.

a 4.6.2 Gesenkgepresste Einschweiß-T-Stücke

a 4.6.2.1 Geltungsbereich

(1) Diese Berechnungsregeln gelten für nahtlose T-Stücke, die durch Pressen im Gesenk aus nahtlosen, gewalzten oder geschmiedeten Rohren hergestellt werden (siehe Bild a 4-8).

(2) Die Maße a und b dürfen die in DIN EN 10253-2 und DIN EN 10253-4 angegebenen Werte für F und G nicht unterschreiten. Für T-Stücke mit Nennweiten größer als DN 300 gelten für die Maße a und b die nachfolgenden Gleichungen:

a ≥ 0,75 d_Ha

(a 4-16)

und

b ≥ 0,5 d_Ha+ 0,25 d_Aa

(a 4-17)

(3) Der äußere Rundungsradius r₂ muss mindestens 0,1 ⋅ d_Aabetragen.

(4) Die Wanddicke soll an keiner Stelle des T-Stückes mehr als das Doppelte und nicht weniger als das 0,875fache der Anschlussnennwanddicke s₁ betragen. Lediglich am Abzweiganschluss darf die Wanddicke über eine maximale Länge von 2 ⋅ s₂auf den Wert 0,875 ⋅ s₂ absinken.

Bild a 4-8: Gepresstes Einschweiß-T-Stück

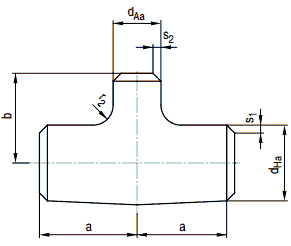
a 4.6.2.2 Berechnungsgrößen und Einheiten

Berechnungsgrößen und Einheiten siehe Abschnitt a 4.7.3 und Bild a 4-8. Zusätzlich gilt:

Formelzeichen	Berechnungsgröße	Einheit
A_p	drucktragende Flächen entsprechend Bild a 4-9	mm²
A_α	tragende Querschnittflächen entsprechend Bild a 4-9 nach Abzug der Wanddicke	mm²
d_Ha	Außennenndurchmesser für Durchgangsanschluss	mm
d_Aa	Außennenndurchmesser für Abzweiganschluss	mm
s_H⁺	Äquivalente Wanddicke für Durchgangsanschluss	mm
s_A⁺	Äquivalente Wanddicke für Abzweiganschluss	mm
s₁	Nennwanddicke für Durchgangsanschluss	mm
s2	Nennwanddicke für Abzweiganschluss	mm
α	Winkel entsprechend Bild a 4-9	Grad

a 4.6.2.3 Berechnung

(1) Mit e_H als größtem Wert von

e_H= d_Ai	(a 4-18)
e_H= 0,5 ⋅ d_Ai+ s_H+ s_A	(a 4-19)
e_H = 0,5 ⋅ d_Ai+ s_a+ r₂⋅(1 - sin α)	(a 4-20)

jedoch maximal e_H= a, und mit e_aals größerem Wert von

e_A = 0,5 ⋅ ((0,5 ⋅ d_Am⋅ s_A)^0,5+ r₂)	(a 4-21)
e_A = r₂ ⋅ cos α,	(a 4-22)

jedoch maximal

e_A = b - (r₂+ s_H) ⋅ cos α - 0,5 ⋅ d_Hi

(a 4-23)

ist die Bedingung

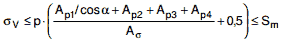(a 4-24)

einzuhalten.

(2) Mit e´_Hals größtem Wert von

e´_H= 0,5 ⋅ (d_Ai+ (0,5 ⋅ d_{Hm ⋅} s_H))^0,5	(a 4-25)
e´_H= 0,5 ⋅ d_Ai+ 2/3 ⋅ (s_H + s_A)	(a 4-26)
e´_H= 0,5 ⋅ d_Ai+ s_A + r₂⋅ (1 - sin α),	(a 4-27)

jedoch maximal e´_H = a, und mit e_awie vor ist zusätzlich die Bedingung

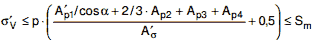(a 4-28)

zu erfüllen.

Die Flächen A_p und A_αsind in Bild a 4-9 dargestellt.

Bild a 4-9: Dimensionierungsflächen für Einschweiß-T-Stück

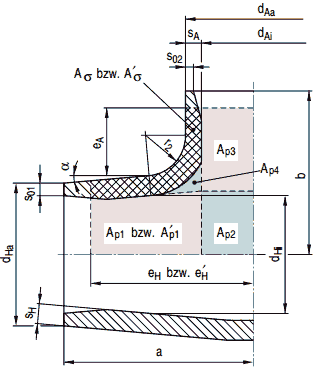
a 4.6.2.4 Äquivalente Anschlusswanddicken

(1) Die für die Spannungsanalyse nach Abschnitt 8.4 benötigten äquivalenten Anschlusswanddicken s⁺_Hund s⁺_aergeben sich mit S als größerem Wert von Ã_V und Ã2_V, (siehe Abschnitt a 4.6.2.3) zu

	p ⋅ d_Ha
s_H⁺=
	2 ⋅ S + p

(a 4-29)

	p ⋅ d_Aa
s_H⁺=		= s_H⁺ / d_Ha
	2 ⋅ S + p

(a 4-30)

(2) Da bedingungsgemäß S kleiner als oder gleich S_m ist, können s_H⁺und s_A⁺auch mit S_m statt S ermittelt werden.

a 4.7 Ausschnittverstärkungen in Rohrleitungen

a 4.7.1 Geltungsbereich

(1) Der Geltungsbereich der nachstehenden Berechnungsregeln ist der unter Abschnitt a 2.2.2.1 aufgeführte Bereich.

(2) Die Berechnungsregeln berücksichtigen die durch inneren Überdruck hervorgerufenen Beanspruchungen. Zusätzliche Kräfte und Momente müssen gesondert berücksichtigt werden.

a 4.7.2 Allgemeines

(1) Ausschnitte sollen rund oder elliptisch sein. Weitere Anforderungen ergeben sich bei Anwendung der Spannungsbeiwerte nach Abschnitt 8.4.

(2) Der Winkel β (siehe Bild a 2.7-8) zwischen Stutzenachse und GrundkÆrperachse soll nicht kleiner als 60 Grad oder größer als 120 Grad sein.

(3) Die Verstärkung eines Ausschnittes in einer Hauptleitung darf wie folgt vorgenommen werden:

durch Wahl einer größeren Wanddicke für die Hauptleitung, als es für die unverschwächte Hauptleitung erforderlich wäre. Diese Wanddicke muss mindestens bis zu einer Länge e_H, von der Ausschnittsachse gemessen, vorhanden sein.
durch Abzweige, die auf einer Länge e_A, von der Außenwand des Grundkörpers gemessen, dickwandiger ausgeführt sind als es für die Innendruckbelastung erforderlich wäre. Der als Verstärkung erforderliche Werkstoff ist gleichmäßig auf den Umfang des Abzweigs zu verteilen.
durch Kombination der unter a) und b) aufgeführten Maßnahmen.

Im Hinblick auf eine beanspruchungsgerechte Formgebung ist c) zu bevorzugen.

(4) Bei mehreren benachbarten Ausschnitten sind die Bedingungen für Verstärkungsflächen für alle Schnittebenen, die durch die Mitte des Abschnitts und senkrecht zur Oberfläche der Hauptleitung gehen, zu erfüllen.

(5) Bei der Verstärkung eines Ausschnittes sind folgende Durchmesser- und Wanddickenverhältnisse einzuhalten:

Ein Wanddickenverhältnis s_A/s_Hist bis maximal 2 zulässig für d_Aikleiner als oder gleich 50 mm. Dies gilt auch für Abzweige mit d_Aigrößer als 50 mm, sofern das Durchmesserverhältnis d_Ai/d_Hikleiner als oder gleich 0,2 ist. Bei Abzweigen mit einem Durchmesserverhältnis d_Ai/d_Higrößer als 0,2 soll s_A/s_Hgrundsätzlich den Wert 1,3 nicht überschreiten. Größere Werte sind erlaubt, wenn

die über vorgenanntes Wanddickenverhältnis hinausgehende, zusätzliche Wanddicke des Abzweigs nicht zur Verstärkung des Stutzenausschnittes herangezogen, sondern aus konstruktiven Gründen gewählt wird oder
der Abzweig mit verkürztem Verstärkungsbereich ausgeführt wird (z.B. Abzweige, die aus Gründen der verbesserten Prüfbarkeit des Rohrleitungsanschlusses konisch ausgebildet sind), wobei die durch die verkürzte Einflusslänge fehlende Verstärkungsfläche im verkürzten Einflussbereich untergebracht werden darf oder
das Verhältnis von Abzweigdurchmesser zum Durchmesser der Hauptleitung kleiner als oder gleich 1: 10 ist.

(6) Eine Ausschnittverstärkung ist nicht erforderlich und der Nachweis für Ausschnitte nach a 4.7.4 muss nicht geführt werden, falls

ein einzelner Ausschnitt einen Durchmesser hat, der gleich oder kleiner als 0,2 ⋅ (0,5 ⋅ d_{Hm ⋅} s_H)^0,5 ist, oder wenn zwei oder mehrere Ausschnitte innerhalb eines Kreises mit dem Durchmesser 2,5 ⋅ (0,5 ⋅ d_{Hm ⋅} s_H)^0,5angeordnet sind, wobei eine Summe der Durchmesser solcher unverstärkten Ausschnitte den Wert von 0,25 ⋅ (0,5 ⋅ d_{Hm ⋅} s_H)^0,5nicht überschreiten darf, und
zwei unverstärkte Ausschnitte keine kleineren Mittenabstände, gemessen auf der Innenseite der Hauptleitung, aufweisen als die Summe ihrer Durchmesser, und
der Rand eines unverstärkten Ausschnitts nicht näher als 2,5 ⋅ (0,5 ⋅ d_{Hm ⋅} s_H)^0,5von der Mitte eines anderen örtlich beanspruchten Bereiches liegt.

Hinweis:
Definition eines örtlich beanspruchten Bereichs siehe Abschnitt 7.7.2.2.

(7) Werkstoffpaarungen

Bestehen Hauptleitung und Abzweig aus Werkstoffen unterschiedlicher zulässiger Spannung, so ist, wenn der Werkstoff der Hauptleitung die kleinere zulässige Spannung aufweist, diese für die Berechnung der gesamten Konstruktion maßgebend. Es muss vorausgesetzt werden, dass das Verformungsvermögen des Abzweigwerkstoffs nicht nennenswert kleiner ist als das des Werkstoffs der Hauptleitung.

Wenn der Abzweigwerkstoff eine geringere zulässige Spannung aufweist, so sind die im Bereich der geringeren zulässigen Spannungen anzuordnenden Verstärkungsflächen im Verhältnis der zulässigen Spannungen zu vergrößern.

Unterschiede bis zu 4 %-Punkten in den Bruchdehnungen der Werkstoffe von Hauptleitung und Abzweig werden als nicht nennenswerter Unterschied des Verformungsvermögens der Werkstoffe angesehen, wobei δ₅ 14 % nicht unterschreiten darf.

Haben Hauptleitungswerkstoff und Abzweigwerkstoff unterschiedliche Wärmedehnungszahlen, so darf ihre Differenz 15 % der Wärmedehnungszahl des Hauptleitungswerkstoffs nicht überschreiten.

a 4.7.3 Berechnungsgrößen und Einheiten

(siehe auch die Bilder a 2.7-2 bis a 2.7-11 und a 4-10 bis a 4-13)

Formelzeichen	Berechnungsgröße	Einheit
d_Ai	Innendurchmesser des Ausschnitts zuzüglich des doppelten Korrosionszuschlags c₂	mm
d_Am	mittlerer Durchmesser des Abzweigs	mm
d_Hi	innerer Durchmesser der Hauptleitung	mm
d_Hm	mittlerer Durchmesser der Hauptleitung	mm
d_n	Nenndurchmesser des konischen Abzweigs	mm
r₁	Innenradius zwischen Abzweig und Hauptleitung	mm
r₂	Mindestradius gemäß Abschnitt 5.2.6
s_A	Nennwanddicke des Abzweigs mit Berücksichtigung der Verstärkung, jedoch abzüglich der Zuschläge c₁und c₂	mm
s_A0	rechnerisch erforderliche Wanddicke des Abzweigs	mm
s_H	Nennwanddicke der Hauptleitung mit Berücksichtigung der Verstärkung, jedoch abzüglich der Zuschläge c₁und c₂	mm
s_H0	rechnerisch erforderliche Wanddicke der Hauptleitung	mm
s_R	Nennwanddicke der Abzweigleitung abzüglich der Zuschläge c₁und c₂	mm
s_R0	rechnerisch erforderliche Wanddicke der Abzweigleitung	mm
y	Maß bei kegeligem Ansatz	mm
α	Neigungswinkel (siehe auch die Bilder a 4-10, a 4-11 und a 4-13)	Grad

Die folgenden Bezeichnungen gehen aus den Bildern a 2.7-8 und a 2.7-9 hervor:

Formelzeichen	Berechnungsgröße	Einheit
A₁, A₂, A₃	für Ausschnittsverstärkungen nutzbare Werkstoffflächen	mm²
e_A	Grenze der Verstärkung senkrecht zur Wand der Hauptleitung	mm
e^H	shalbe Breite des Verstärkungsbereichs, längs der Mittelebene der Hauptleitung gemessen	mm
e´_H	halbe Breite des Bereichs, in dem 2/3 der Verstärkung liegen sollen	mm
β	Winkel zwischen den Achsen des Abzweigs und der Hauptleitung	Grad

a 4.7.4 Berechnung

a 4.7.4.1 Erforderliche Verstärkung

(1) Die gesamte Querschnittsfläche a einer Verstärkung, die in jeder Ebene für ein Rohr unter Innendruck erforderlich ist, muss der folgenden Bedingung genügen:

a ≥ d_Ai ⋅ s_H0 ⋅ (2 - sinβ)

(a 4-31)

(2) Mindestens die Hälfte der erforderlichen Verstärkungsfläche muss auf jeder Seite der Stutzenachse vorhanden sein.

a 4.7.4.2 Zulässige mittragende Längen

(1) Die mittragende Länge der Hauptleitung ist wie folgt zu ermitteln:

e_H = d_Ai

(a 4-32)

oder

e_H= 0,5 ⋅ d_Ai+ s_H+ s_A

(a 4-33)

Der größere der beiden Werte ist der Berechnung zugrunde zu legen. Zusätzlich gilt, dass 2/3 der Verstärkungsfläche innerhalb eines Bereiches der Länge 2
⋅ e´_Hliegen müssen (Bilder a 2.7-8 und a 2.7-9), wobei

e´_H= der größere Wert ist von entweder

e´_H = 0,5 ⋅ [d_Ai+ (0,5 ⋅ d_Hm ⋅ s_H)^1/2]

(a 4-34)

oder

	S_A
e´_H = 0,5 ⋅ d_Ai+		+ S_H
	sinβ

(a 4-35)

(2) Die mittragende Länge des zylindrischen Abzweigs ist wie folgt zu ermitteln:

e_a= 0,5 ⋅ [(0,5 ⋅ d_Am⋅ s_A)^1/2+ r₂]

(a 4-36)

worin

d_Am= d_Ai + s_A

(a 4-37)

ist.

Siehe auch die Bilder a 4-10, a 4-11, a 4-12.

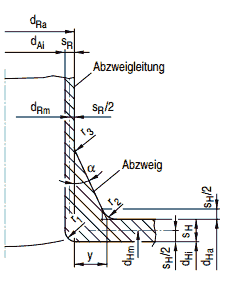
(3) Die mittragende Länge des konischen Abzweigs ist wie folgt zu ermitteln:

e_A = 0,5 ⋅ (0,5 ⋅ d_n⋅ s_A)^1/2

(a 4-38)

worin

d_n= d_Ai+ s_R+ y ⋅ cosα

(a 4-39)

ist.

Siehe auch Bild a 4-13.

Für die Abzweige mit konischem Innendurchmesser ist d_niterativ zu ermitteln.

a 4.7.4.3 Beanspruchungsschema für nutzbare Verstärkungsflächen

Die für die Erfüllung der Gleichung (a 4-31) nutzbaren Verstärkungsflächen A₁, A₂, A₃sind in den Bildern a 2.7-8 und a 2.7-9 dargestellt; sie müssen die Bedingung A₁ + A₂+ A₃größer als oder gleich a erfüllen.

Bild a 4-10: Abzweig

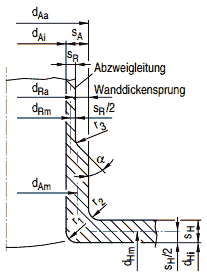
Bild a 4-11: Abzweig

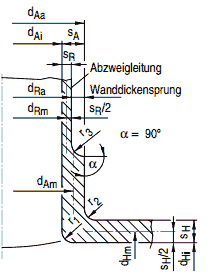
Bild a 4-12: Abzweig

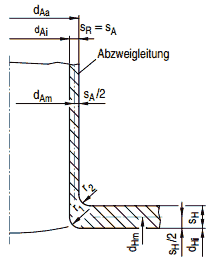
Bild a 4-13: Abzweig

Anforderungen an den Primärspannungsnachweis bei erneuten rechnerischen Nachweisen

Anhang B

B 1 Allgemeines

(1) Dieser Anhang beschreibt qualitativ und methodisch eine alternative Nachweismöglichkeit bei erneuten rechnerischen Primärspannungsnachweisen unter den in Abschnitt B 2 beschriebenen Voraussetzungen, falls die Anforderungen an die Dimensionierung unter Zugrundelegung der Auslegungsstufe (Stufe 0) nicht erfüllt sind. Er ist nicht auf Primärspannungsnachweise für neue Systeme und Komponenten anwendbar.

Hinweis:
Im Sinne einer transparenten Nachweisführung werden die technischen Gründe für die Notwendigkeit der Anwendung des Anhangs B (z.B. Regelwerksänderung, neue Kenntnisse über die Einwirkungen) in den Nachweisunterlagen benannt.

(2) Die Bestimmung der allgemeinen primären Membranspannungen hat bei erneuten rechnerischen Nachweisen grundsätzlich nach Abschnitt 6 zu erfolgen.

(3) Auf Basis des Kenntnisstands über die möglichen Lastfälle werden die zugrunde zu legenden Werte für Nachweisdruck, Nachweistemperatur und zusätzliche Nachweislasten genauer festgelegt. Die Anwendbarkeit der Werte ist zu begründen.

Hinweis:
Abhängig vom Kenntnisstand über die möglichen Lastfälle ist die Festlegung mehrerer Datensätze für Nachweisdruck, Nachweistemperatur und zusätzliche Nachweislasten möglich.

(4) Bei einem erneuten rechnerischen Primärspannungsnachweis darf die Nachweisführung gemäß Abschnitt B 3 angewendet werden.

(5) Wenn die Nachweisführung gemäß Abschnitt B 3 angewendet wird, sind der Nachweis und die hierbei verwendeten Nachweislasten in der Anlagendokumentation unter Einhaltung der Anforderungen gemäß KTA 1404 so zu dokumentieren, dass zu einem späterem Zeitpunkt keine Lasten oberhalb der nachgewiesenen Werte als zulässig erachtet werden.

B 2 Voraussetzungen

(1) Die erneut zu bewertende Komponente erfüllt ansonsten die Grundsätze der Basissicherheit.

(2) Die Sicherheitsventile und sonstige Sicherheitseinrichtungen sind so eingestellt, dass der Druck im bestimmungsgemäßen Betrieb den Nachweisdruck nur kurzfristig über- schreitet und dabei die Beanspruchungsgrenzen von Stufe B eingehalten werden.

(3) Ein eventueller Entfall von Zuschlägen bei der Auslegung nach VPU 1 (z.B. Abdeckung des maximalen Druckes eines spezifizierten Lastfalls durch den Auslegungsdruck) ist sicherheitstechnisch begründet.

(4) Bei Verwendung von Ist-Abmessungen ist die Methodik der Messung und Auswertung im Rahmen der Nachweisführung anzugeben.

B 3 Nachweisführung

(1) Die Daten des Lastfalls bestehen aus den gemäß B 1 (3) festgelegten Werten für den Nachweisdruck, die Nachweistemperatur und die zu berücksichtigenden zusätzlichen Nachweislasten.

(2) Der Nachweisdruck für eine Komponente oder ein Bauteil ist mindestens die größte Druckdifferenz zwischen den druckbelasteten Oberflächen gemäß Stufe A.

(3) Die Nachweistemperatur dient der Festlegung der Festigkeitskennwerte. Sie soll mindestens gleich der nach Stufe a für den mechanisch führenden Lastfall gemäß (2) und (4) an der zu betrachtenden Stelle zu erwartenden Wandtemperatur sein.

(4) Die zusätzlichen Nachweislasten müssen bei Überlagerung mit dem Nachweisdruck mindestens so hoch angesetzt werden, dass sie die gleichzeitig wirkenden ungünstigsten primären Beanspruchungen der Stufe a abdecken.

(5) Der Primärspannungsnachweis ist

mit den Einwirkungen gemäß (2) bis (4) in Anlehnung an Abschnitt 6 unter Einhaltung der Beanspruchungsgrenzen der Stufe 0 und
für die Beanspruchungsstufen B, C, D und P unter Einhaltung der Beanspruchungsgrenzen der jeweiligen Stufe

gemäß Tabelle 7.7-4, 7.7-5 und 7.7-6 zu erbringen, wobei die geometrischen Ist-Werte des Bauteils (z.B. Wanddicke) verwendet werden dürfen.

(6) Die Analyse des mechanischen Verhaltens darf entweder durch eine allgemeine Analyse gemäß Abschnitt 7 oder durch eine komponentenspezifische Analyse gemäß Abschnitt 8 nachgewiesen werden.

Rechnerische Methoden

Anhang C

Die im Folgenden behandelten Methoden dienen der Ermittlung der das mechanische Verhalten kennzeichnenden Größen (z.B. Schnittkräfte, Spannungen, Verformungen) infolge von Belastungen. Sie beruhen entweder auf theoretisch abgeleiteten oder auf versuchsmäßig ermittelten Beziehungen für das mechanische Verhalten.

Die infrage kommenden Berechnungsmethoden unterscheiden sich in der Art der zugrunde gelegten Beziehungen, in der Anpassungsfähigkeit an die Geometrie, die Belastungsart und das Werkstoffverhalten, in der Form ihrer Lösungsansätze und Behandlung der auftretenden Gleichungssysteme, in der Aussagefähigkeit der Ergebnisse und im Aufwand.

C 1 Stufenkörpermethode (SKM)

C 1.1 Anwendungsbereich

C 1.1.1 Allgemeines

Die Stufenkörpermethode (SKM) ermöglicht die Berechnung von Beurteilungsgrößen für die Festigkeit (z.B. Spannungen) und für das Verformungsverhalten (Verschiebungen und Verdrehungen). Die Unterteilung einer Gesamtstruktur in Stufenkörper setzt voraus, dass sich für jeden Stufenkörper der Zusammenhang zwischen seinen Randverformungen einerseits und den Belastungen sowie den an seinen Rändern wirkenden Schnittgrößen andererseits angeben lässt. Bei der Verwendung von Differentialgleichungen wird die Einteilung in Stufenkörper im Allgemeinen so vorgenommen, dass die Lösungen der verwendeten Differentialgleichungen jeweils im gesamten Stufenkörpersystem gelten.

Bei der SKM wird vorausgesetzt, dass der Verlauf von Verformungs- und Schnittgrößen über einen Querschnitt durch entsprechende Größen in einem ausgezeichneten Punkt dieses Querschnittes repräsentiert werden kann und sich aus diesen repräsentativen Größen die lokalen Größen mittels Annahmen (z.B. linearer Verlauf über die Wanddicke) ableiten lassen. Diese Annahmen müssen von der Aufgabenstellung her zulässig sein.

Die SKM wird vornehmlich auf lineare Probleme angewendet.

C 1.1.2 Geometrie der Bauteile

Die SKM wird vorwiegend für die statische Berechnung verwendet, die sich beispielsweise aus Rotationsschalen, Kreisplatten, Kreisscheiben und Stülpringen zusammensetzen.

Geometrische Vereinfachungen der Stufenkörper und die Behandlung gegebener Strukturen mittels der Differentialgleichungen für geeignete Ersatzstrukturen sind zulässig, sofern diese Art der Idealisierung zu hinreichend genauen oder konservativen Ergebnissen führt.

Bezüglich der Querschnittsgeometrie der Stufenkörper ist die Berücksichtigung von Anisotropie möglich, z.B. doppelwandige Schalen mit Versteifungen, orthotrope Schalen etc.

C 1.1.3 Mechanische Belastungen und Randbedingungen

Bei der SKM ergeben sich außer den in Abschnitt C 1.1.1 gemachten Voraussetzungen prinzipiell keine weiteren Einschränkungen bezüglich der Erfassung mechanischer Belastungen und Randbedingungen. Allerdings gelten nur in Verbindung mit rotationssymmetrischen Belastungen und Randbedingungen verhältnismäßig einfache Gleichungen für den Spannungs- und Verformungszustand der einzelnen rotationssymmetrischen Stufenkörper. Auch nichtrotationssymmetrische Belastungen und Randbedingungen lassen sich mit Hilfe von Fourier-Reihen berücksichtigen: der Rechenaufwand vervielfacht sich mit der Anzahl der erforderlichen Fourier-Koeffizienten.

Außerdem können Anfangsverzerrungen, wie z.B. thermische Dehnungen berücksichtigt werden.

C 1.1.3.1 Örtliche Erstreckung der Belastung

Die mechanischen Belastungen können in Form von Punkt-, Linien-, Flächen- und Volumenlasten berücksichtigt werden.

C 1.1.3.2 Zeitlicher Verlauf der Belastung

Beliebig zeitabhängige Belastungen können prinzipiell mit der SKM behandelt werden. Dabei können die üblichen Methoden der Dynamik angewandt werden.

C 1.1.4 Kinematisches Verhalten der Struktur

Bei der Anwendung der SKM wird im Allgemeinen kinematisch vollständig lineares Verhalten angenommen. Dies bedeutet, dass die Verformungen als klein gegenüber den geometrischen Abmessungen angenommen und die Gleichgewichtsbedingungen am unverformten Element aufgestellt werden (Theorie 1. Ordnung).

C 1.1.5 Werkstoffverhalten

In den meisten Fällen wird lineares Werkstoffverhalten (lineare Spannungs-Dehnungsbeziehung), gegebenenfalls Berücksichtigung der Temperaturabhängigkeit der Konstanten und unter Berücksichtigung von Anfangsdehnungen, angenommen. Der Werkstoff wird meist als homogen und isotrop vorausgesetzt.

Die Berücksichtigung nichtlinearen Werkstoffverhaltens ist prinzipiell mit im Allgemeinen größerem Aufwand möglich.

C 1.2 Grundlagen

C 1.2.1 Vorbemerkung

Die Grundlagen der SKM werden hier insoweit erläutert, als sie für die Anwendung der SKM und die Beurteilung der Rechenergebnisse wesentlich sind. Diese Erläuterungen dienen auch der Bestimmung der hier verwendeten Begriffe.

Wie jedem thermomechanischen Berechnungsverfahren liegen auch der SKM die physikalischen Prinzipien der Kontinuumsmechanik zugrunde. Diese Prinzipien werden bei der SKM exakt oder näherungsweise erfüllt.

C 1.2.2 Grundlegende Begriffe und physikalische Prinzipien

C 1.2.2.1 Felder

In den Kontinuumstheorien werden die physikalischen Eigenschaften von Körpern durch Felder beschrieben (z.B. Verschiebungsfeld, Geschwindigkeitsfeld, Temperaturfeld u. a.), die zumindest stückweise als stetige Funktionen der Ortskoordinaten und gegebenenfalls der Zeit angesehen werden.

Wie in Abschnitt C 1.1.1 angegeben, werden die Felder nur mittels repräsentativer, dem Querschnitt zugeordneter Größen dargestellt.

C 1.2.2.2 Kinematische Beziehungen

Die Stetigkeit des Verschiebungsfeldes bedeutet bei Tragwerken, deren Deformation nur durch die Verschiebungsgrößen einer Fläche oder einer Linie beschrieben wird, (Platten und Schalen bzw. Balken) auch, dass an jedem Punkt der Bezugsfläche oder -linie nicht nur die Verschiebungen, sondern auch die Verdrehungen um zwei in der Fläche oder drei im Raum liegende Achsen stetig sind.

Ist ein Verschiebungsfeld stetig und erfüllt es die kinematischen Randbedingungen, so bezeichnet man es als kinematisch verträglich.

Beispiel für kinematische Randbedingungen:

starre Einspannungen
starre Auflager
vorgeschriebene Randverschiebungsgrößen.

Bei gleitenden Lagerungen ist die Bedingung der Nullverschiebung senkrecht zur Gleitfläche kinematisch, bei gelenkiger Lagerung die Bedingung der Null-Verschiebung der Gelenke (nicht jedoch die Bedingung der Spannungs- oder Kräftefreiheit).

Die Deformation in der unmittelbaren Umgebung eines Punktes des Tragwerkes wird durch Verzerrungen (Längenänderung eines Linienelementes, Winkeländerung zwischen zwei Linienelementen) beschrieben. Die Voraussetzung für einen linearen Zusammenhang zwischen den Verschiebungen sind kleine Verzerrungen und Verdrehungen, wobei die Größenordnung der Verdrehungen höchstens gleich der Größenordnung der Verzerrungsquadrate ist; sind diese Voraussetzungen gegeben, so liegt geometrische Linearität vor.

C 1.2.2.3 Erhaltungssätze

Für einen Teil oder die Gesamtheit des Tragwerkes sind zu jedem Zeitpunkt der Impuls- und der Impulsmomentensatz sowie statische Randbedingungen erfüllt. Für quasistationäre mechanische Vorgänge führt dies auf die inneren Gleichgewichtsbedingungen:

Summe der Kräfte am (deformierten) Volumenelement ist gleich Null.
Summe der Momente am (deformierten) Volumenelement ist gleich Null.

Diese Beziehungen verbinden die Volumenkräfte mit den Ableitungen der Spannungen nach den Ortskoordinaten. Bei dynamischen Problemen müssen die Beiträge der Trägheitskräfte zu den Volumenkräften berücksichtigt werden.

Randbedingungen, die Werte für Kraftgrößen vorschreiben, werden statische Randbedingungen genannt.

Beispiele für statische Randbedingungen:

Rand belastet durch Flächenlast, Linienlast oder Punktlast,
lastfreier Rand ohne sonstige Bedingungen,
Bedingung für Reibungskräfte in gleitenden Lagern,
Bedingung für Momentenfreiheit eines gelenkigen Auflagers.

An allen Punkten mit statischen Randbedingungen herrscht Gleichgewicht zwischen den von außen angreifenden konzentrierten oder verteilten Kräften und Momenten einerseits und den entsprechenden inneren Kräften und Momenten oder Spannungskomponenten andererseits; die äußeren Kraftgrößen können dabei Null sein.

Die Gleichgewichtsbedingungen sind gleichwertig mit dem Prinzip der virtuellen Arbeit; dieses lässt sich folgendermaßen formulieren:

Ist ein Körper im Gleichgewicht, so ist die äußere virtuelle Arbeit, die von der äußeren Belastung (einschließlich der Volumenkräfte) mit virtuellen Verschiebungen geleistet wird, gleich der inneren virtuellen Arbeit, die von den Spannungen mit den virtuellen Verzerrungen geleistet wird.

Dabei sind virtuelle Verschiebungen kleine, kinematisch zulässige, sonst jedoch beliebige Verschiebungen; virtuelle Verzerrungen leiten sich aus den virtuellen Verschiebungen über die üblichen Verschiebungs-Verzerrungs-Beziehungen ab. Für dynamische Probleme gilt als Erweiterung das Lagranged´Alembert´sche Prinzip, das man aus dem Prinzip der virtuellen Arbeit durch Hinzunahme der Trägheitskräfte erhält.

Unterliegt das Tragwerk neben mechanischen Belastungen auch thermischen (Temperaturausgleich), so ist zur Beschreibung eines physikalischen Verhaltens der Impuls- und Impulsmomentensatz durch den Energiesatz zu ergänzen. Dieser lässt sich folgendermaßen formulieren:

Die zeitliche Änderung der Summe aus innerer und kinetischer Energie des Volumenelements ist gleich der Summe der Leistungen von Oberflächen- und Volumenkräften am Element und der pro Zeiteinheit zugeführten thermischen Energie.

Diese Bedingung stellt unter Einbeziehung der Impulssätze den Zusammenhang zwischen der zeitlichen Änderung der Temperatur im Element und den räumlichen Ableitungen der Wärmeflüsse her.

Sind für die Belastungen des Tragwerkes auch strömungstechnische Vorgänge maßgebend (wie es z.B. in Rohrleitungen der Fall sein kann), so ist für das strömende Medium außer den Erhaltungssätzen von Impuls und Energie der Erhaltungssatz für die Masse (Kontinuitätsgleichung) zu erfüllen.

Die differentielle Formulierung der Erhaltungssätze führt auf im Allgemeinen partielle Differentialgleichungen für die den momentanen Zustand des physikalischen Systems beschreibenden Feldgrößen (Verschiebungen, Verschiebungsgeschwindigkeit, Temperatur etc.).

C 1.2.2.4 Materialgesetze

Für das mechanische Verhalten eines Werkstoffs gibt das Materialgesetz den Zusammenhang zwischen Spannungen und Verzerrungen linear an, während z.B. bei elastoplastischem Verhalten das Materialgesetz nichtlinear ist. Bei elastisch isotropen Stoffen lässt sich das Materialverhalten mit zwei voneinander unabhängigen Koeffizienten beschreiben. Elastisch anisotrope Stoffe werden in allgemeinen mit der SKM nicht behandelt.

Zusätzliche Parameter sind erforderlich bei thermischer Belastung (Wärmeausdehnungszahl, Wärmeleitzahl, temperaturabhängige elastische Moduln etc.) und bei strömenden Medien (Wärmeübergangszahl, Viskosität, etc.).

C 1.2.3 Prinzipien der Methode

C 1.2.3.1 Grundgedanke

Der Grundgedanke der SKM besteht darin, die zu untersuchende Struktur als statisch oder dynamisch unbestimmtes System von Teilstrukturen (Stufenkörper) aufzufassen, die sich unter den gegebenen Belastungen und Randbedingungen nicht unabhängig voneinander, sondern unter der zusätzlichen Wirkung gegenseitiger mechanischer Beeinflussung verformen.

C 1.2.3.2 Mechanisches Verhalten des einzelnen Stufenkörpers

Die SKM verwendet für den einzelnen Stufenkörper Matrizenbeziehungen zwischen Verformungsgrößen und Kraftgrößen. Diese Beziehungen können theoretisch oder experimentell gewonnen werden.

Die betreffenden Differentialbeziehungen sind aus dem Impuls- und Impulsmomentensatz, dem kinematischen Zusammenhang zwischen Verzerrungen und Verformungen sowie dem Werkstoffgesetz abzuleiten.

Außer den gegebenen Lasten (äußeren Kraftgrößen) sowie Druck- und Temperaturverteilungen müssen erforderlichenfalls an einem Rand oder mehreren Rändern des betrachteten Stufenkörpers zusätzliche, statisch bestimmte Kraftgrößen angebracht werden, um diesen für sich ins Gleichgewicht zu setzen. Diese Zusatzkraftgrößen sind demnach ebenfalls bekannt und müssen zur Erhaltung des Gleichgewichts der Gesamtstruktur mit umgekehrtem Vorzeichen am benachbarten Rand des anschließenden Stufenkörpers angebracht werden.

Die aus den gegebenen Lasten, den Druck- und Temperaturverteilungen und den bekannten Zusatzkraftgrößen resultierenden Verformungen werden als bekannte Verformungen bezeichnet.

Liegen Differentialgleichungen für die betreffenden Stufenkörper vor, die deren mechanisches Verhalten beschreiben, so lassen sich hierfür unter Einhaltung der Randbedingungen durch Integration analytische oder numerische Lösungen entwickeln. Sie liefern in Form von Matrizenbeziehungen den Zusammenhang zwischen den bekannten Zustandgrößen (Kräften, Momenten, Verschiebungen und Verdrehungen) an jedem Ort des betreffenden Stufenkörpers. Diese Beziehungen können auch mittels anderer mathematischer Methoden oder auf experimentellem Wege gefunden werden.

C 1.2.3.3 Mechanisches Zusammenwirken der Stufenkörper im System

Werden die einzelnen Stufenkörper eines Systems gegebenen Lasten und Zusatzkräften unterworfen, so erfährt jeder Stufenkörper - für sich betrachtet - Verformungen gemäß Abschnitt C 1.2.3.2.

Die am einzelnen Stufenkörper angreifenden Lasten und Zusatzkraftgrößen stehen dabei zwar jeweils miteinander im Gleichgewicht, aber die Verformungen benachbarter Stufenkörper erfüllen im Allgemeinen zunächst nicht die Verträglichkeitsbedingungen.

Zur Herstellung der Verträglichkeit ist deshalb die Anbringung geeigneter, zusätzlicher, unbestimmter Kraft- und Verformungsgrößen erforderlich, deren Größe und Richtung aus der gegenseitigen mechanischen Beeinflussung aller Stufenkörper des Stufenkörpersystems zu bestimmen sind. Die Gleichungen dieses Systems werden mittels Gleichgewichtsbedingungen oder mit Hilfe des Prinzips der virtuellen Arbeit, diesmal auf das gesamte Stufenkörpersystem angewandt, abgeleitet.

Die Beziehungen für die unbekannten Kraft- oder Verformungsgrößen bilden je nach Berechnungsverfahren ein System simultaner Gleichungen für sämtliche Kraft- oder Verformungsgrößen der Gesamtstruktur oder bei Verwendung von Übertragungsmatrizen ein Gleichungssystem zur Verknüpfung der Zustandsvektoren an den Rändern (z.B. Anfang und Ende) der Struktur. In diesem Falle lassen sich aus den unter Einhaltung der dort vorliegenden Randbedingungen und berechneten Zustandsgrößen an den Rändern der Gesamtstruktur die unbekannten Größen innerhalb der Gesamtstruktur nacheinander ermitteln.

C 1.2.3.4 Resultierende Kraft- und Verformungsgrößen

Die aus dem Gleichungssystem sich ergebenden Lösungen für die unbekannten Kraft- oder Verformungsgrößen liefern zusammen mit den bekannten Kraft- oder Verformungsgrößen die daraus resultierenden Kraft- und Verformungsgrößen. Verformungen und zugehörige Spannungen sind zu beurteilen.

C 1.2.3.5 Eigenschaften der Lösungen

Die mit der SKM errechneten Lösungen stellen aus mehreren Gründen Näherungen dar.

In den verwendeten Differentialgleichungen können Vernachlässigungen enthalten sein, die vorgenommen wurden, um entweder überhaupt eine analytische Lösung zu ermöglichen oder um eine vereinfachte analytische Lösung zu erhalten (z.B. Kontinuum als dünne Schale betrachtet). Die Vernachlässigungen in den Differentialgleichungen selbst müssen auf physikalischen, geometrischen Voraussetzungen beruhen, die von der Problemstellung und vom Berechungsverfahren her erlaubt sind.
Die geschlossene Lösung der Differentialgleichung kann z.B. hinsichtlich der Randbedingungen oder der Belastung eine Näherung darstellen, oder sie gilt nur in einem eingeschränkten Definitionsbereich.
Wenn die Lösung der Differentialgleichungen durch numerische Integration gefunden wird, hängt die Genauigkeit von der Ordnung der Approximation und der Schrittweite ab.
Das Gleichungssystem für das elastische Zusammenwirken der Stufenkörper im System kann schlecht konditioniert sein, z.B. dann, wenn die Stufenkörperlänge klein gegenüber der Abklinglänge ist.

C 1.3 Anwendung

C 1.3.1 Idealisierung

C 1.3.1.1 Idealisierung der Struktur

Die Gesamtstruktur wird näherungsweise durch eine Reihe aneinander anschließender Stufenkörper ersetzt, deren mechanisches Verhalten, soweit es die beabsichtigte Aussagefähigkeit der Ergebnisse erfordert, demjenigen der gegebenen Struktur entspricht. Die Meridianlängen der Stufenkörper sind in Abhängigkeit von dem Näherungscharakter der verwendeten Differentialgleichungen und ihrer Lösungsansätze sowie den Abklinglängen von Randstörungen und der Numerik der zugehörigen Gleichungssysteme zu wählen.

C 1.3.1.2 Idealisierung der Lasten

Die einzelnen Stufenkörper werden zunächst als voneinander unabhängig betrachtet und den gegebenen äußeren Einflüssen, wie z.B. Druck- und Temperaturverteilungen, sowie den gegebenen Lasten (äußeren Rand-Kräften und -Momenten) ausgesetzt. Wenn das verwendete physikalische Modell nicht die exakte Erfassung des gegebenen Lastangriffs ermöglicht, kann dieser näherungsweise auch durch ein geeignetes, statisch äquivalentes Kraftgrößensystem ersetzt werden; hierbei getroffene Vereinfachungen müssen von der Problemstellung her zulässig sein.

Die Aufteilung von Randlasten auf diejenigen Ränder benachbarter Stufenkörper, in deren gemeinsamer Schnittebene sie wirken, kann in beliebiger Weise vorgenommen werden.

Außer den gegebenen Lasten müssen erforderlichenfalls an einem Rand oder mehreren Rändern des betrachteten Stufenkörpers zusätzliche, statisch bestimmte Kraftgrößen angebracht werden, um diesen für sich ins Gleichgewicht zu setzen. Die Zusatzkraftgrößen sind demnach ebenfalls bekannt und müssen zur Erhaltung des Gleichgewichts der Gesamtstruktur mit umgekehrten Vorzeichen am benachbarten Rand des anschließenden Stufenkörpers angebracht werden.

C 1.3.1.3 Idealisierung der Randbedingungen

Auch die Idealisierung der statischen und kinematischen Randbedingungen kann nicht auf exakte Weise vorgenommen werden, wenn die infrage kommenden Randbedingungen von den verwendeten Berechnungsansätzen nicht exakt erfasst werden. Dies trifft z.B. zu

für rotationsunsymmetrische Randbedingungen mit geringer Abweichung von der Rotationssymmetrie bei Berechnungsansätzen für rein rotationssymmetrische Belastungen,
für Belastungen von Flächen mit geringer Erstreckung in einer Richtung, wenn jene als Linienlasten idealisiert werden,
für Verschiebungen längs einer gekrümmten Kurve, die durch einen Polygonzug angenähert wird.

Derartige Näherungen müssen von der Problemstellung her zulässig sein.

C 1.3.1.4 Kontrolle der Eingabedaten

Eine Kontrolle der Eingabedaten ist unerlässlich und sollte, soweit möglich, anhand der programmintern gespeicherten Daten durchgeführt werden.

Routinen zur Prüfung der Eingabedaten sowie graphische Darstellung der Eingabedaten, z.B. der Geometrie, der Randbedingungen und der Belastungen, sind zweckmäßig.

C 1.3.2 Programme

C 1.3.2.1 Allgemeines

Rechnungen nach der SKM werden im Allgemeinen mit Programmen auf Datenverarbeitungsanlagen durchgeführt.

C 1.3.2.2 Dokumentation der Programme

Zu jedem verwendeten Programm muss eine Dokumentation vorliegen.

Darin müssen folgende Punkte beschrieben oder angegeben sein:

Kennzeichnung des Programms einschließlich Änderungszustand,
theoretische Grundlagen,
Anwendungsbereich und Voraussetzungen,
Beschreibung der Programmorganisation, soweit für die Benutzung und Beurteilung des Programms erforderlich,
Eingabevorschrift zur Programmsteuerung und Problembeschreibung,
Erläuterung der Ausgabe,
Anwendungsbeispiele.

Im theoretischen Teil der Dokumentation müssen alle dem Programm zugrunde liegenden theoretischen Grundlagen ausreichend angegeben sein.

Erforderlichenfalls ist die entsprechende Literatur aufzuführen. Im Teil Anwendungsbeispiele müssen demonstrative und überprüfte Berechnungsbeispiele für die Anwendung enthalten sein.

C 1.3.2.3 Zuverlässigkeit der Programme

Im Falle umfangreicher SKM-Programme kann die Fehlerfreiheit für alle möglichen Rechenwege nicht ohne weiteres vorausgesetzt werden. Deshalb sind zur Beurteilung der Zuverlässigkeit folgende Gesichtspunkte zu berücksichtigen:

modularer Aufbau des Programms,
standardisierte Programmsprache,
zentrale Programmwartung,
großer Benutzerkreis und häufiger Programmeinsatz, insbesondere für den vorliegenden Anwendungsbereich.

Das zuverlässige Arbeiten des Programms kann in dem Maße erwartet werden, in dem die genannten Gesichtspunkte für die jeweilige Programmversion erfüllt sind.

C 1.3.3 Beurteilung von Rechenergebnissen

C 1.3.3.1 Allgemeines

Der erste Schritt bei der Beurteilung von Rechenergebnissen ist stets die Prüfung, ob die Ergebnisse physikalisch einleuchtend sind. Diese Plausibilitätskontrolle stellt eine notwendige, aber nicht hinreichende Bedingung für die Verwendbarkeit der Ergebnisse dar. Zusätzlich ist deshalb die Überprüfung des Rechenmodells, der Richtigkeit der Daten und der einwandfreien Arbeitsweise und Anwendung des Programms erforderlich.

C 1.3.3.2 Physikalische Kontrolle

Bei der SKM erstreckt sich die physikalische Kontrolle der Ergebnisse auf die Überprüfung folgender Lösungseigenschaften:

Verträglichkeitsbedingungen,
Gleichgewichtsbedingungen,
Randbedingungen,
Symmetriebedingungen,
Spannungen und Verformungen im ungestörten Bereich,
Abklingen von Randstörungen.

C 1.3.3.3 Numerische Kontrolle

C 1.3.3.3.1 Untersuchung der Ergebnisse numerischer Lösungsverfahren

Ein häufig verwendetes Verfahren zur numerischen Lösung von Differentialgleichungen ist z.B. die Methode von Runge-Kutta. Sie hat mit vielen anderen schrittweise durchzuführenden Näherungsverfahren gemeinsam, dass die Genauigkeit der Lösung in starkem Maße von der Ordnung der berücksichtigten Ableitungen und von der gewählten Schrittweite abhängt. Eine Abschätzung des absoluten Fehlers ist innerhalb des Runge-Kutta-Verfahrens nicht möglich. Konvergieren jedoch die Näherungslösungen mit abnehmender Schrittweite gegen die exakte Lösung, so lässt sich durch Vergleich zweier Näherungslösungen, die mit unterschiedlicher Schrittweite gewonnen werden, eine relative Genauigkeit angeben.

C 1.3.3.3.2 Prüfung des Berechnungsverfahrens

Bei der SKM können numerische Fehler im Wesentlichen bei der Lösung großer Gleichungssysteme, infolge der Anwendung von numerischen Lösungsverfahren für den einzelnen Stufenkörper (z.B. der numerischen Integration) oder infolge der Anwendung des Übertragungsmatrizenverfahrens auf das Stufenkörpersystem, entstehen. In solchen Fällen muss die numerische Genauigkeit geprüft werden.

C 1.3.3.3.3 Untersuchung des Lösungsvektors

Einsetzen der Elemente des Lösungsvektors in die ursprünglich aufgestellten Gleichungen gibt Auskunft über die Größenordnung des numerischen Fehlers, sofern die Koeffizientenmatrix hinreichend gut konditioniert ist.

C 1.3.3.4 Vergleich mit Ergebnissen aus anderen Untersuchungen

C 1.3.3.4.1 Allgemeines

Zur Beurteilung der Ergebnisse von Rechnungen nach der SKM können als Ergänzung oder als Ersatz für andere Kontrollen herangezogen werden:

Vergleiche mit anderen Rechnungen nach der SKM,
Vergleiche mit Rechnungen nach anderen Berechnungsverfahren und
Vergleiche mit experimentell ermittelten Ergebnissen.

Die Wahl des für den Vergleich zu verwendenden Untersuchungsverfahrens hängt davon ab, wo der Schwerpunkt der Kontrolle liegen soll (theoretische Formulierung, Programmierung, Idealisierung, Eingabedaten und ggf. numerische Genauigkeit).

Für die Vergleichsrechnung ergibt sich die Möglichkeit der Benutzung gleicher oder verschiedener Programme, Betriebssysteme, Datenverarbeitungsanlagen und Idealisierungen.

C 1.3.3.4.2 Vergleich mit anderen Rechnungen nach der SKM

Durch den Vergleich der Ergebnisse einer Rechnung nach der SKM mit Ergebnissen anderer Rechnungen nach der SKM können in Abhängigkeit vom benutzten Programm und von der gewählten Idealisierung die theoretische Formulierung, Programmierung, Idealisierung, Eingabedaten und numerische Genauigkeit der Berechnung beurteilt werden.

Die numerische Genauigkeit der Berechnung kann u. U. verbessert werden, wenn die Stellenzahl entsprechend erhöht oder wenn im Falle der numerischen Integration die Schrittweite verkleinert wird.

Die Güte der Idealisierung kann durch Vergleichsrechnung mit anderen im Allgemeinen feineren oder das mechanische Verhalten des Bauteils exakter erfassenden Idealisierungen überprüft werden.

Die theoretische Formulierung lässt sich zusammen mit der Programmierung durch Vergleichsrechnungen unter Verwendung von Programmen mit anderen theoretischen Grundlagen überprüfen, wenn dabei die gleiche Idealisierung und Stellenzahl verwendet wird.

Vergleichsrechnungen mit gleichen oder verschiedenen Programmen und gleichen Idealisierungen dienen der Kontrolle der Eingabedaten, wenn diese unabhängig erstellt wurden.

C 1.3.3.4.3 Vergleich mit Rechnungen nach anderen Berechnungsverfahren

Soweit andere Berechnungsverfahren, z.B. die FDM gemäß Abschnitt C 2 oder die FEM gemäß Abschnitt C 3 die Voraussetzungen zur Behandlung des jeweils vorliegenden Problems bieten, können sie zu Vergleichsrechnungen herangezogen werden. Diese Vergleichsrechnungen dienen dann zur summarischen Beurteilung aller Eigenschaften beider Lösungen.

C 1.3.3.4.4 Vergleich mit experimentell ermittelten Ergebnissen

Die Beurteilung der Ergebnisse von Rechnungen nach der SKM kann teilweise oder vollständig durch den Vergleich mit experimentell ermittelten Werten erfolgen, wobei die Eigenarten und Grenzen der Messverfahren zu berücksichtigen sind.

Die Messergebnisse können aus Messungen am Modell (z.B. spannungsoptische Untersuchungen) oder aus Messungen am Bauteil (Dehnungs- oder Verschiebungsmessungen) gewonnen werden, soweit alle wesentlichen Parameter simuliert werden können. Bei Verwendung von Modellen müssen diese für das gestellte Problem repräsentativ sein.

Dieser Vergleich dient insbesondere der Beurteilung der Zulässigkeit von Annahmen, die der SKM zugrunde liegen.

C 2 Methode der finiten Differenzen (FDM)

C 2.1 Anwendungsbereich

Die FDM ermöglicht die Berechnung von Beurteilungsgrößen für die Festigkeit (z.B. Spannungen) und für das Verformungsverhalten (Verschiebungen und Verdrehungen). Die im Folgenden hauptsächlich für strukturmechanische Probleme aufgestellten Anforderungen lassen sich sinngemäß auf Probleme der Wärmeübertragung, der Strömungsmechanik und auf gekoppelte Probleme anwenden.

Mit dieser Methode ist es möglich, sowohl beliebige Geometrien und Belastungen, als auch beliebiges Struktur- und Werkstoffverhalten zu erfassen.

Vereinfachungen zur Durchführung der Rechnungen bezüglich des geometrischen Modells, des Werkstoffverhaltens, der Lastannahmen und des kinematischen Verhaltens sind auf die Fragestellung abzustellen und sinnvoll aufeinander abzustimmen.

C 2.1.2 Geometrie der Bauteile

Die Geometrie des zu untersuchenden Bauteils kann ein-, zwei- und dreidimensional berücksichtigt werden.

Der Erfassung der Geometrie sind unter Umständen Grenzen gesetzt durch die Kapazität der Datenverarbeitungsanlage oder des einzelnen Programms sowie durch den erforderlichen Aufwand.

C 2.1.3 Mechanische Belastungen und Randbedingungen

Bei der FDM ergeben sich praktisch keine Einschränkungen bezüglich der Art der mechanischen Belastungen und Randbedingungen eines Bauteils.

Außerdem können Anfangsverzerrungen wie z.B. thermische Dehnungen berücksichtigt werden.

C 2.1.3.1 Örtliche Erstreckung der Belastung

Die mechanischen Belastungen können in Form von Punkt-, Linien-, Flächen- und Volumenlasten berücksichtigt werden.

C 2.1.3.2 Zeitlicher Verlauf der Belastung

Beliebige zeitabhängige Belastungen können prinzipiell mit der FDM behandelt werden. Dabei können die üblichen Methoden der Dynamik bei der FDM angewandt werden.

C 2.1.4 Kinematisches Verhalten der Struktur

Prinzipiell ist beliebiges kinematisches Verhalten der Struktur darstellbar, wobei dann gegebenenfalls große Verdrehungen und große Verzerrungen sowie Spiele berücksichtigt werden müssen.

Im Allgemeinen beschränkt man sich auf kinematisch vollständig lineares Verhalten der Struktur.

Falls erforderlich kann man primäre Instabilitäten erfassen (Knicken und Beulen).

C 2.1.5 Werkstoffverhalten

In den meisten Fällen beschränkt man sich auf lineares Werkstoffverhalten (lineare Spannungs-Dehnungs-Beziehung), gegebenenfalls unter Berücksichtigung der Temperaturabhängigkeit der Konstanten und unter Berücksichtigung von Anfangsdehnungen.

Die Berücksichtigung nichtlinearen Werkstoffverhaltens (z.B. starrplastisch, linear elastisch - ideal plastisch, allgemein elastoplastisch, viskoelastisch) ist mit meist größerem Aufwand möglich.

C 2.2 Grundlagen der FDM

C 2.2.1 Vorbemerkung

Die Grundzüge der FDM werden hier insoweit erläutert, als sie für die Anwendung der FDM und die Beurteilung der Rechenergebnisse wesentlich sind. Diese Erläuterungen dienen auch der Bestimmung der hier verwendeten Begriffe.

Wie jedem thermomechanischen Berechnungsverfahren liegen auch der FDM die physikalischen Prinzipien der Kontinuumsmechanik zugrunde. Diese Prinzipien werden bei der FDM je nach der Wahl der Diskretisierungsmethode auf verschiedene Weise exakt oder näherungsweise erfüllt.

C 2.2.2 Grundlegende Begriffe und physikalische Prinzipien

C 2.2.2.1 Felder

C 2.2.2.2 Kinematische Beziehungen

Dort, wo sich ein Tragwerk als Kontinuum verhält, ist das Verschiebungsfeld in seinem Innern zu jedem Zeitpunkt stetig. Durch kinematische Randbedingungen werden Werte für Verschiebungsgrößen an Rändern des Berechnungsgebietes vorgeschrieben. Erfüllt ein Verschiebungsfeld sowohl die Stetigkeitsforderung als auch die kinematischen Randbedingungen, so bezeichnet man es als kinematisch verträglich (kinematisch zulässig).

Die Stetigkeit des Verschiebungsfeldes bedeutet bei Tragwerken, deren Deformation nur durch die Verschiebungsgrößen einer Fläche oder einer Linie beschrieben wird (Platten und Schalen bzw. Balken), dass an jedem Punkt der Bezugsfläche oder -linie nicht nur die Verschiebungen, sondern auch die Verdrehungen um zwei in der Fläche oder drei im Raum liegende Achsen stetig sind.

Beispiele für kinematische Randbedingungen:

starre Einspannungen,
starre Auflager,
vorgeschriebene Randverschiebungsgrößen.

Bei gleitenden Lagerungen ist die Bedingung der Nullverschiebung senkrecht zur Gleitfläche kinematisch, bei gelenkiger Lagerung ist die Bedingung der Null-Verschiebung der Gelenke (nicht jedoch die Bedingung der Spannungs- oder Kräftefreiheit) kinematisch.

Die Deformation in der unmittelbaren Umgebung eines Punktes des Tragwerkes wird durch Verzerrungen (Längenänderung eines Linienelementes, Winkeländerung zwischen zwei Linienelementen) beschrieben. Die Voraussetzungen für einen linearen Zusammenhang zwischen den Verschiebungen und den Verzerrungen sind kleine Verzerrungen und Verdrehungen, wobei die Größenordnung der Verdrehungen höchstens gleich der Größenordnung der Verzerrungsquadrate ist; sind diese Voraussetzungen gegeben, so liegt geometrische Linearität vor.

C 2.2.2.3 Erhaltungssätze und Gleichgewichtsbedingungen

Summe der Kräfte am (deformierten) Volumenelement ist gleich Null.
Summe der Momente am (deformierten) Volumenelement ist gleich Null.

Diese Bedingungen verbinden die Volumenkräfte mit den Ableitungen der Spannungen nach den Ortskoordinaten. Bei dynamischen Problemen müssen die Beiträge der Trägheitskräfte zu den Volumenkräften berücksichtigt werden.

Randbedingungen, die Werte für Kraftgrößen vorschreiben, werden statische Randbedingungen genannt. Beispiele für statische Randbedingungen:

Rand belastet durch Flächenlast, Linienlast oder Punktlast,
lastfreier Rand ohne sonstige Bedingungen,
Bedingung für Reibungskräfte in gleitenden Lagern,
Bedingung für Momentenfreiheit eines gelenkigen Auflagers.

An allen Punkten mit statischen Randbedingungen stehen die inneren Spannungen oder Kräfte mit den angreifenden äußeren Belastungen, die Null sein können, im Gleichgewicht.

Die Gleichgewichtsbedingungen sind gleichwertig mit dem Prinzip der virtuellen Arbeit; dieses lässt sich folgendermaßen formulieren:

Dabei sind virtuelle Verschiebungen kleine, kinematisch zulässige, sonst jedoch beliebige Verschiebungen. Virtuelle Verzerrungen leiten sich aus den virtuellen Verschiebungen über die üblichen Verschiebungs-Verzerrungs-Beziehungen ab. Für dynamische Probleme gilt als Erweiterung das Lagranged´Alembert´sche Prinzip, das man aus dem Prinzip der virtuellen Arbeit durch Hinzunahme der Trägheitskräfte erhält.

Unterliegt das Tragwerk neben mechanischen Belastungen auch thermischen (Temperaturausgleich), so ist zur Beschreibung seines physikalischen Verhaltens der Impuls- und der Impulsmomentensatz durch den Energiesatz zu ergänzen. Dieser lässt sich folgendermaßen formulieren:

Diese Bedingung stellt unter Einbeziehung der Impulssätze den Zusammenhang zwischen der zeitlichen Änderung der Temperatur im Element und den räumlichen Ableitungen der Wärmeflüsse her.

Sind für die Belastungen des Tragwerkes auch strömungsmechanische Vorgänge maßgebend (wie es z.B. in Rohrleitungen der Fall sein kann), so ist für das strömende Medium außer den Erhaltungssätzen von Impuls und Energie der Erhaltungssatz für die Masse (Kontinuitätsgleichung) in Rechnung zu stellen.

C 2.2.2.4 Materialgesetze

Für das mechanische Verhalten eines Festkörpers gibt das Materialgesetz den Zusammenhang zwischen Spannungen und Verzerrungen an. Bei linearelastischem Materialverhalten ist dieser Zusammenhang linear, während z.B. bei elastoplastischem Verhalten das Materialgesetz nichtlinear ist. Bei linearelastischen, isotropen Stoffen lässt sich das Materialverhalten mit zwei voneinander unabhängigen Koeffizienten beschreiben, bei linearelastischen, anisotropen Stoffen können bis zu 21 voneinander unabhängige Koeffizienten erforderlich werden.

Das Materialgesetz für ein Fluid liefert einen Zusammenhang zwischen den Zustandsgrößen, z.B. für ideales Gas zwischen Druck, Dichte und Temperatur (thermische Zustandsgleichung).

C 2.2.3 Diskretisierung

C 2.2.3.1 Vorgehensweise

Die Darstellung des Tragwerks als Rechenmodell wird als Idealisierung bezeichnet.

Ausgangspunkt für die FDM sind die das Problem beschreibenden Differentialgleichungen. Diese Differentialgleichungen werden numerisch gelöst, indem die Differentialquotienten durch Differenzenquotienten ersetzt werden und damit das Problem der Integration eines Differentialgleichungssystems auf die Auflösung eines algebraischen Gleichungssystems zurückgeführt wird (Diskretisierung).

Entsprechend der Art der Auflösung der Gleichungssysteme unterscheidet man indirekte und iterative Differenzenverfahren.

Ferner unterscheidet man nach der Form der Differenzenausdrücke, d. h. nach dem Grad des Ansatzes, gewöhnliche und verbesserte Differenzenverfahren.

Das zu untersuchende System wird entweder einheitlich als Berechnungsgebiet betrachtet oder in Teilberechnungsgebiete zerlegt, die miteinander gekoppelt werden. Jedes Berechnungsgebiet wird mit einem Netz von Stützstellen überzogen.

Bei bestimmten Verfahren werden für die verschiedenen Felder unterschiedliche Stützstellen gewählt, weil hierdurch die Aufstellung der Differenzenquotienten erleichtert wird.

Der in der infinitesimalen Theorie kontinuierlich veränderliche Ortsvektor wird somit durch einen endlichen Satz von diskreten Ortsvektoren ersetzt, die nur an den Stützstellen des Rechennetzes (den Knotenpunkten) definiert sind. Entsprechend werden kontinuierliche Felder durch endliche, diskrete Sätze von Funktionswerten (diskrete Feldkomponenten) an den Knoten, ggf. auch an Zwischenpunkten, angenähert.

Die Genauigkeit der Lösungen von Differenzengleichungen im Vergleich zu den exakten Lösungen der Differentialgleichungen hängt u. a. von der algebraischen Verknüpfung der diskreten Feldkomponenten ab. Welcher Genauigkeitsgrad einem räumlichen Differenzenquotienten zukommt, lässt sich z.B. dadurch erkennen, dass man die Differentialoperation und die ihr zugeordnete Differenzenoperation auf eine räumliche Welle (Fourier-Mode) anwendet und die Ergebnisse vergleicht. Unterscheiden sich beide Ergebnisse nur in quadratischen und höheren Termen des Verhältnisses der räumlichen Ausdehnung einer Zelle des Netzes zur Wellenlänge des Modes, so wird diese Näherung als Approximation zweiter Ordnung bezeichnet. Bei hinreichend kleinen Werten dieses Verhältnisses reicht die Approximation zweiter Ordnung meist aus. Die größte zulässige Maschenweite richtet sich nach der kleinsten Wellenlänge des zu approximierenden Feldes (Langwellenapproximation).

Diese Entscheidungshilfe ist nicht auf lineare Probleme beschränkt, da die nichtlinearen Probleme sich meist durch stückweise lineare Zustandsänderungen annähern lassen. Bei nichtlinearem Verhalten ist jedoch in Rechnung zu stellen, dass aufgrund der Abhängigkeit der materiellen Kenngrößen (wie Moduln und Dichte) von der Größe der Beanspruchung auch die Wellenlängen beeinflusst werden. Bezüglich der Genauigkeit gilt auch hier, dass die kleinste auftretende Wellenlänge die Maschenweite des Stützstellennetzes festlegt.

Für die Diskretisierung der Zeitvariablen bei Vorgängen, die sowohl von den Raumkoordinaten als auch von der Zeit abhängen, lassen sich ähnliche Kriterien gewinnen, indem die Differenzengleichung auf einen räumlich und zeitlich veränderlichen Fourier-Mode angewendet wird. Die sich ergebende Beziehung zwischen Ausbreitungsgeschwindigkeit und Wellenlänge (Dispersionsbeziehung) hängt dabei außer von der Maschenweite des (räumlichen) Stützstellennetzes auch vom Zeitschritt (d. h. von den Stützstellen im Zeitbereich) ab. Durch geeignete Wahl der Größe des Zeitschritts lässt sich (zumindest in bestimmten Frequenzbereichen) die Dispersionsbeziehung der Differentialgleichung annähern.

Je nach der Form der algebraischen Verknüpfung der diskreten Feldkomponenten in den Differenzenquotienten ergeben sich explizite oder implizite Verfahren zur Lösung der Differenzengleichungen. Ein Lösungsverfahren wird dabei als explizit bezeichnet, wenn die diskreten Feldkomponenten zu einem Zeitpunkt sich direkt, ohne dass ein Gleichungssystem aufzulösen ist, aus den für frühere Zeitpunkte bekannten Werten der Komponenten berechnen lassen; ist dies nicht der Fall, spricht man von einem impliziten Lösungsverfahren.

Implizite Algorithmen erfordern im Allgemeinen mehr Rechenaufwand als explizite; dieser höhere Aufwand kann jedoch hinsichtlich der Genauigkeit und Stabilität der Lösungen (siehe Abschnitt C 2.3.2) gerechtfertigt sein.

C 2.2.3.2 Eigenschaften der Lösungen

Die mit FDM errechneten Lösungen stellen in zweierlei Hinsicht Näherungslösungen dar:

(1) Physikalische Diskretisierung

Wegen der Beschränkung der Anzahl der möglichen Freiheitsgrade durch die Diskretisierung des Kontinuums können die für das Problem maßgebenden physikalischen Prinzipien im Allgemeinen nicht exakt erfüllt sein. Damit die Näherungslösungen die physikalischen Vorgänge hinreichend genau wiedergeben können, sind folgende Forderungen an ein Differenzenverfahren zu stellen:

Konsistenz
Grenzübergänge zu infinitesimalen Zellenausdehnungen und Zeitintervallen müssen die Differenzengleichungen auf die zu lösenden Differentialgleichungen zurückführen. Dabei ist zu beachten, dass es raum- und zeitschrittabhängige Differenzengleichungen gibt, die unter Umständen je nach Wahl der Inkremente zu verschiedenen Differentialgleichungen konvergieren (inflexibles im Gegensatz zum flexiblen Differenzenschema).
Stabilität
Der Differenzenalgorithmus muss so konzipiert sein, dass sich die Diskretisierungsfehler nicht akkumulieren. Bei zeitabhängigen Problemen lässt sich im Prinzip für jedes Differenzenverfahren eine Matrix (Verstärkungsmatrix) angeben, die den Fehler zu einem gewissen Zeitpunkt mit dem Fehler zu einem früheren Zeitpunkt verknüpft. Stabilität der Lösungen ist dann gewährleistet, wenn die Beträge sämtlicher Eigenwerte der Verstärkungsmatrix kleiner oder höchstens gleich Eins sind. Diese Forderung ist (vor allem bei nichtlinearen Differenzensystemen) nicht immer für jeden Wertebereich der relevanten Parameter oder Parameterfunktionen (Zeitschritt-, Zellgröße, konstitutive Gleichungen etc.) zu erfüllen, sondern häufig nur für gewisse, beschränkte Bereiche dieser Größen. In diesen Fällen ist der Differenzenalgorithmus nur bedingt stabil.
Konvergenz
Die Lösung der Differenzengleichungen muss gegen die exakte Lösung konvergieren, wenn die Raum- und Zeitinkremente gegen Null streben. Werden die Differentialgleichungen eines mit korrekten Anfangs- und Randbedingungen versehenen Problems durch konsistente Differenzengleichungen approximiert, so ist die Stabilität der Differenzenlösung notwendig und hinreichend für die Konvergenz.

Weicht die Gestalt der diskretisierten Struktur von der tatsächlichen Gestalt merklich ab, so können hierdurch Ungenauigkeiten entstehen. In vielen Fällen ändert die Annäherung gekrümmter Konturen durch stückweise gerade oder ebene Elemente die diskreten Feldkomponenten nur unwesentlich, doch können aus den Feldkomponenten abgeleitete Größen, wie z.B. Verzerrungs- und Spannungskomponenten, an solchen künstlichen Knickstellen nur schwer interpretiert werden.

(2) Numerische Approximation

Für eine gegebene physikalische Diskretisierung weicht die numerische Lösung von der exakten ab. Diese Abweichung hat zwei Ursachen:

Wegen der beschränkten Stellenzahl in der Datenverarbeitungsanlage entstehen Anfangsabbrechfehler und Rundungsfehler. Dies kann sich besonders bei Systemen mit extrem unterschiedlichen physikalischen Eigenschaften im Rechenmodell auswirken. Durch Berechnung von Konditionszahlen, die eine Abschätzung der Vergrößerung des Anfangsabbrechfehlers durch die Rundungsfehler gestatten, kann man eine untere, oft sehr konservative Schranke für die Zahl der numerisch exakten Stellen bekommen.
Bei bestimmten Algorithmen, z.B. der iterativen Gleichungsauflösung oder der iterativen Lösung des Eigenwertproblems, verbleibt ein Fehler, der von einer vorgegebenen Genauigkeitsschranke abhängt.

C 2.3 Anwendung der FDM

C 2.3.1 Idealisierung

C 2.3.1.1 Umfang der Idealisierung

Mechanische Probleme können sowohl global, als auch im Detail berechnet werden. Die Anforderungen an die Ergebnisse bestimmen den Aufwand der Idealisierung. Durch Auswahl der Differenzenapproximation, Festlegung der Stützstellen in Raum und Zeit und Idealisierung der Randbedingungen wird die Qualität der Näherung entscheidend beeinflusst.

C 2.3.1.2 Differenzenapproximation

Die Eignung der Differenzenapproximation für die Problemklasse und die problembedingten Randbedingungen (z.B. Lasteinleitung, Lastverteilung, Lagerung) ist im Hinblick auf die Aufgabenstellung zu beachten.

C 2.3.1.3 Festlegung der Stützstellen

Lage und Anzahl der Stützstellen sollen so gewählt werden, dass das Rechenergebnis für die jeweilige Aufgabenstellung genügend genau ist. Für die Anordnung der Stützstellen ist auch der Einfluss der Differenzenapproximation zu berücksichtigen. Dabei ist folgendes zu beachten:

Erfordert die Aufgabenstellung der Berechnung die Kenntnis stark veränderlicher Feldkomponenten, z.B. Verformungen oder Spannungen, so ist die Feinheit des Stützstellennetzes entsprechend zu wählen.
Die Grenzen zwischen verschiedenen maßgebenden Materialeigenschaften müssen beachtet werden.
Sowohl starke Unregelmäßigkeiten in der (räumlichen) Anordnung der Stützstellen als auch starke Unterschiede in den maßgeblichen Eigenschaften von Stützstelle zu Stützstelle können sich in einer Verschlechterung der Konditionierung der Gleichungsmatrix auswirken.
Das Stützstellennetz muss eine im Rahmen der Aufgabenstellung hinreichend genaue Abbildung der eingeprägten Kräfte und sonstiger Belastungen und Randbedingungen ermöglichen. Die Einhaltung gewisser Randbedingungen kann eine von der Kontur abweichende Anordnung von Randstützstellen erforderlich machen.
Für dynamische Probleme muss das Netz so gestaltet werden, dass das dynamische Verhalten der Struktur der Berechnung zugänglich wird. Zahl und Art der Freiheitsgrade müssen so gewählt werden, dass die interessierenden Bewegungsformen beschrieben werden können.
Die Idealisierung der Struktur soll so erfolgen, dass keine lokalen oder globalen Singularitäten der Steifigkeitsmatrix auftreten. Andernfalls müssen diese im Lösungsalgorithmus berücksichtigt werden.
Die Behandlung lokaler Fast-Singularitäten (nach Maßgabe der Konditionierung und Rechengenauigkeit) darf nicht zur Verfälschung des physikalischen Verhaltens der Struktur führen. Bei Fast-Singularitäten ist besonders auf hinreichende numerische Genauigkeit der Ergebnisse zu achten.
Aus physikalischen Gründen, z.B. Materialabtrennung oder Durchdringung, oder aus numerischen Gründen (schlechte Konditionierung des Gleichungssystems, z.B. in stark verzerrten Netzen bei Lagrange-Darstellung) kann es notwendig werden, das Stützstellennetz im Laufe der Rechnung teilweise oder ganz neu festzulegen.

C 2.3.1.4 Formulierung der Randbedingungen

Die Randbedingungen können Bedingungen für äußere Kraft- und Verschiebungsgrößen umfassen; sie können aber auch aus Schnittbedingungen an gedachten Schnitträndern bestehen. Dies ist z.B. bei Detailuntersuchungen und bei Anwendung von Symmetriebedingungen der Fall; dadurch dürfen jedoch die Ergebnisse im Hinblick auf die Aufgabenstellung nicht unzulässig verändert werden. Lastveränderlichen Randbedingungen ist vor allem im Hinblick auf Nichtlinearitäten besondere Beachtung zu schenken.

C 2.3.1.5 Festlegung der Last- oder Zeitinkremente

Die Last- oder Zeitinkremente sind so zu wählen, dass der Verlauf der diskreten Feldkomponenten über dem Lastparameter oder über der Zeit für die jeweilige Aufgabenstellung genügend genau erfasst wird, und dass die numerische Stabilität der Lösung gewährleistet ist. Die Inkremente können im Lauf einer Rechnung verändert werden. Dabei ist es je nach Problemklasse und Differenzenapproximation bei manchen Verfahren zweckmäßig, nur allmähliche Veränderung zuzulassen.

C 2.3.1.6 Kontrolle der Eingabedaten

Wegen der normalerweise großen Menge der Eingabedaten ist eine Kontrolle unerlässlich. Diese sollte soweit möglich anhand programmintern gespeicherter Daten durchgeführt werden.

Routinen zur Prüfung der Eingabedaten sowie graphische Darstellung der Eingabedaten, z.B. der Geometrie, der Randbedingungen und der Belastungen, sind zweckmäßig.

C 2.3.2 Programme

C 2.3.2.1 Allgemeines

Rechnungen nach der FDM werden wegen der damit verbundenen hohen Anzahl von Rechenoperationen nur mit Programmen auf Datenverarbeitungsanlagen durchgeführt.

C 2.3.2.2 Dokumentation der Programme

Zu jedem verwendeten Programm muss eine Dokumentation vorliegen. Darin müssen folgende Punkte beschrieben oder angegeben sein:

Kennzeichnung des Programms, einschließlich Änderungszustand,
theoretische Grundlagen,
Anwendungsbereich und Voraussetzungen,
Beschreibung der Programmorganisation, soweit für die Benutzung und Beurteilung erforderlich,
Eingabevorschriften zur Programmsteuerung und Problembeschreibung,
Erläuterung der Ausgabe,
Anwendungsbeispiele.

Im theoretischen Teil der Dokumentation müssen alle dem Programm zugrunde liegenden theoretischen Grundlagen ausreichend angegeben sein. Erforderlichenfalls ist die entsprechende Literatur aufzuführen.

Im Teil Anwendungsbeispiele müssen demonstrative und überprüfte Berechnungsbeispiele für die Anwendung enthalten sein.

C 2.3.2.3 Zuverlässigkeit der Programme

Wegen des Umfangs der FDM-Programme kann die Fehlerfreiheit nicht ohne weiteres für alle möglichen Rechenwege vorausgesetzt werden. Deshalb sind zur Beurteilung der Zuverlässigkeit folgende Gesichtspunkte zu berücksichtigen:

modularer Aufbau des Programms,
standardisierte Programmsprache,
zentrale Programmwartung,
großer Benutzerkreis und häufiger Programmeinsatz, ins

besondere für den vorliegenden Anwendungsbereich.

Das zuverlässige Arbeiten des Programms kann in dem Maß erwartet werden, in dem die genannten Gesichtspunkte für die jeweilige Programmversion erfüllt sind.

C 2.3.3 Beurteilung von Rechenergebnissen

C 2.3.3.1 Allgemeines

Der erste Schritt bei der Beurteilung von Rechenergebnissen ist stets die Prüfung, ob die Ergebnisse physikalisch einleuchtend sind. Diese Prüfung ist umso aussagekräftiger, je besser die Gesamtheit der Ergebnisse zu überblicken ist. Die Plausibilität der Ergebnisse stellt eine notwendige Bedingung für ihre Brauchbarkeit dar. Zusätzlich sind die Eignung des Rechenmodells, die Richtigkeit der Daten und die einwandfreie Arbeitsweise und Anwendung des Programms zu überprüfen.

Da jede mit diskretisierenden numerischen Verfahren erhaltene Lösung eine Näherung des physikalischen Verhaltens darstellt, ist zu prüfen, ob die Güte der Näherung für das gestellte Problem ausreicht. Sofern die Gültigkeit der Diskretisierung und der numerischen Verfahren durch diese Kontrollen nachgewiesen werden soll, so können diese in dem Umfang entfallen, in dem sie bereits bei direkt vergleichbaren anderen Rechnungen durchgeführt wurden. Direkt vergleichbar sind Probleme, bei denen sowohl die Struktur als auch die Belastungen qualitativ gleich sind, und bei denen alle Parameter, die die Berechnung charakterisieren, ungefähr übereinstimmen.

C 2.3.3.2 Physikalische Kontrolle

C 2.3.3.2.1 Vorbemerkung

Wie bereits in Abschnitt C 2.2.3.1 dargestellt, liefert die FDM Komponenten der betrachteten Feldgrößen nur an diskreten Stellen. Dies kann gegebenenfalls eine Interpretation der gegebenen diskreten Lösung durch Inter- oder Extrapolation erforderlich machen (Beispiel: Randbedingungen oder Kopplung von Berechnungsteilgebieten).

C 2.3.3.2.2 Stetigkeit- und Monotonieanforderungen an die diskreten Feldkomponenten

Bei den meisten Problemklassen des betrachteten Anwendungsbereichs der FDM müssen die Feldkomponenten in Bereichen mit kontinuierlicher Geometrie sowie mit konstanten oder kontinuierlich variierenden Materialkennwerten und Belastungen einen stetigen und stückweise monotonen Verlauf sowohl im Raum als auch über der Zeit zeigen. Bei manchen Problemen gilt dies auch für gewisse Ableitungen der Feldkomponenten (siehe Abschnitt C 2.2.2.2). Weisen in solchen Bereichen die entsprechenden diskreten Feldkomponenten oder die entsprechenden Ableitungen davon stärkere Oszillationen auf, so muss überprüft werden, ob eine Instabilität vorliegt. Ausnahmen zu dem oben beschriebenen Verlauf der Feldkomponenten stellen z.B. ausgedehnte "Randstörungen" bei bestimmten Schalen oder Stoßwellen dar.

C 2.3.3.2.3 Erfüllung der Erhaltungssätze und der Materialgesetze

Die Erhaltungssätze werden von der exakten Lösung lokal und global erfüllt, von der FDM-Lösung, von bestimmten Verfahren abgesehen, jedoch nur global. Dies kann sowohl an der Diskretisierung, als auch an der speziellen Wahl der Differenzenoperatoren liegen. Zumindest im letzteren Fall ist zu überprüfen, ob der Fehler in den Erhaltungsgrößen, z.B. im Impuls oder in der Energie, wenigstens global in einem dem jeweiligen Problem angemessenen Rahmen bleibt. Eine solche Überprüfung der Erhaltungsgrößen muss auch vorgenommen werden, wenn während des Rechenablaufs das Stützstellennetz neu festgelegt wird (siehe Abschnitt C 2.3.1.3 g). Treten in der Lösung Unstetigkeiten auf, so muss zu der globalen Kontrolle eine lokale treten, deren Kontrollvolumina die jeweilige Unstetigkeit enthalten. Bei Problemen mit nichtlinearen Materialgesetzen ist auf deren Einhaltung zu achten.

C 2.3.3.3 Numerische Kontrolle

C 2.3.3.3.1 Vorbemerkung

Grundsätzlich wird der Fehler durch eine feinere Unterteilung der zu untersuchenden Struktur infolge der physikalischen Diskretisierung verringert, die Anfälligkeit für numerische Fehler im Allgemeinen erhöht. Wenigstens bei expliziten Verfahren macht eine Verfeinerung der Diskretisierung im Raum aus Gründen der Stabilität in der Regel auch eine Verkleinerung der Zeit- oder Lastschritte erforderlich.

Lässt die Diskretisierung Anfälligkeit für numerische Fehler erwarten, so muss die numerische Güte der Lösung geprüft werden. (Fehler infolge der physikalischen Diskretisierung sind in diesem Zusammenhang nicht angesprochen, siehe Abschnitt C 2.2.3.2).

Der Einfluss der Anfangsabbrech- und Rundungsfehler kann verringert werden, indem die gesamte Rechnung von Beginn an (und nicht erst bei der Auflösung der Systemgleichung) mit größerer Anzahl gültiger Stellen durchgeführt wird.

C 2.3.3.3.2 Untersuchung des Lösungsvektors

Einsetzen der Komponenten des Lösungsvektors in das ursprüngliche Gleichungssystem gibt bei impliziten Differenzenverfahren Auskunft über die Größenordnung des numerischen Fehlers.

C 2.3.3.3.3 Kontrolle auf numerische Instabilität

Numerische Instabilität aufgrund unpassend gewählter Diskretisierung führt im Allgemeinen auf Ergebnisse, die die in Abschnitt C 2.3.3.2.2 dargelegten Monotonieforderungen verletzen. Sie ist deshalb leicht zu erkennen. Bei bestimmten Problemklassen (dissipative Systeme) kann eine verdeckte Instabilität vorliegen. Dies kann z.B. durch Nachrechnung mit feinerer Diskretisierung überprüft werden. Dabei ist zu beachten, dass auch numerische Verfahren dissipative Eigenschaften zeigen können.

C 2.3.3.3.4 Kontrolle mittels Konditionszahlen

Konditionszahlen gestatten, obere Schranken für die Größe der Gesamtheit der Anfangsabbrech- und Rundungsfehler anzugeben, jedoch nicht für die Fehler in den einzelnen Komponenten des Lösungsvektors.

C 2.3.3.4 Vergleich mit Ergebnissen aus anderen Untersuchungen

C 2.3.3.4.1 Allgemeines

Zur Beurteilung der Ergebnisse von Rechnungen nach der FDM können als Ergänzung oder als Ersatz der Kontrollen gemäß den Abschnitten C 2.3.1.6, C 2.3.2.3, C 2.3.3.1, C 2.3.3.2 und C 2.3.3.3 herangezogen werden:

Vergleiche mit anderen FDM-Rechnungen,
Vergleiche mit Rechnungen nach anderen Berechnungsverfahren und
Vergleiche mit experimentell ermittelten Ergebnissen.

Die Wahl des für den Vergleich zu verwendenden Untersuchungsverfahrens ist in Abhängigkeit davon zu treffen, wo der Schwerpunkt der Kontrolle liegen soll (theoretische Formulierung, Programmierung, Idealisierung, Eingabedaten oder numerische Genauigkeit).

C 2.3.3.4.2 Vergleich mit anderen FDM-Rechnungen

Durch den Vergleich der Ergebnisse einer Rechnung nach der FDM mit Ergebnissen anderer Rechnungen nach der FDM können je nach Wahl der Idealisierung sowie des Programms, der Datenverarbeitungsanlage und des Betriebssystems einzelne oder alle Eigenschaften der FDM-Lösung beurteilt werden.

Bei der Überprüfung der Programmzuverlässigkeit durch Vergleichsrechnungen ist ein unabhängiges Programm und dieselbe Diskretisierung zu verwenden.

Die numerische Genauigkeit kann verbessert werden, wenn die Stellenzahl entsprechend erhöht wird.

Die Gültigkeit der Idealisierung kann durch Vergleichsrechnung mit anderen Idealisierungen überprüft werden.

Vergleichsrechnungen mit gleichen oder verschiedenen Programmen und gleichen Idealisierungen dienen der Kontrolle der Eingabedaten, wenn diese unabhängig erstellt wurden.

C 2.3.3.4.3 Vergleich mit Rechnungen nach anderen Berechnungsverfahren

Soweit andere Berechnungsverfahren, z.B. die FEM oder die Stufenkörpermethode die Voraussetzungen zur Behandlung des jeweils vorliegenden Problems bieten, können sie zu Vergleichsrechnungen herangezogen werden. Diese Vergleichsrechnungen dienen dann zur globalen Beurteilung aller Eigenschaften der FDM-Lösungen.

C 2.3.3.4.4 Vergleich mit experimentell ermittelten Ergebnissen

Die Beurteilung der Ergebnisse von Rechnungen nach der FDM kann teilweise oder vollständig durch den Vergleich mit experimentell ermittelten Werten erfolgen, wobei die Eigenarten und Grenzen der Messverfahren zu berücksichtigen sind. Die Messergebnisse können aus Messungen am Modell (z.B. aus spannungsoptischen Untersuchungen) oder aus Messungen am Bauteil (Dehnungs- oder Verschiebungsmessungen) gewonnen werden, soweit alle wesentlichen Parameter simuliert werden können. Bei Verwendung von Modellen müssen diese für das gestellte Problem repräsentativ sein. Dieser Vergleich dient insbesondere der Beurteilung der Zuverlässigkeit der physikalischen Annahmen, die der Idealisierung zugrunde liegen.

C 3 Methode der finiten Elemente (FEM)

C 3.1 Anwendungsbereich

C 3.1.1 Allgemeines

Die Methode der finiten Elemente (FEM) ermöglicht die Berechnung von Beurteilungsgrößen für die Festigkeit (z.B. Spannungen) und für das Verformungsverhalten (Verschiebungen und Verdrehungen). Die im folgenden hauptsächlich für strukturmechanische Probleme aufgestellten Anforderungen lassen sich sinngemäß auf Probleme der Wärmeübertragung, der Strömungsmechanik und auf gekoppelte Probleme anwenden.

Mit dieser Methode ist es möglich, sowohl beliebige Geometrien und Belastungen als auch beliebiges Struktur- und Werkstoffverhalten zu erfassen.

Vereinfachungen zur Durchführung der Rechnung bezüglich des geometrischen Modells, des Werkstoffverhaltens, der Lastannahmen und des kinematischen Verhaltens sind auf die Fragestellung abzustellen und sinnvoll aufeinander abzustimmen.

C 3.1.2 Geometrie der Bauteile

Die Geometrie des zu untersuchenden Bauteils kann ein-, zwei- und dreidimensional berücksichtigt werden.

Der Erfassung der Geometrie sind unter Umständen Grenzen gesetzt durch die Kapazität der Datenverarbeitungsanlage oder des einzelnen Programms sowie durch den erforderlichen Aufwand.

C 3.1.3 Mechanische Belastungen und Randbedingungen

Bei der FEM ergeben sich praktisch keine Einschränkungen bezüglich der Art der mechanischen Belastungen und Randbedingungen eines Bauteils. Außerdem können Anfangsverzerrungen, wie z.B. thermische Dehnungen berücksichtigt werden.

C 3.1.3.1 Örtliche Erstreckung der Belastung

Die mechanischen Belastungen können in Form von Punkt-, Linien-, Flächen- und Volumenlasten berücksichtigt werden.

C 3.1.3.2 Zeitlicher Verlauf der Belastung

Beliebige zeitabhängige Belastungen können prinzipiell mit der FEM behandelt werden. Dabei können die üblichen Methoden der Dynamik bei der FEM angewandt werden.

C 3.1.4 Kinematisches Verhalten der Struktur

Prinzipiell ist beliebiges kinematisches Verhalten der Struktur darstellbar, wobei dann gegebenenfalls große Verdrehungen und große Verzerrungen sowie Spiele berücksichtigt werden müssen.

Im Allgemeinen wird kinematisch vollständig lineares Verhalten der Struktur angenommen.

Falls erforderlich kann man primäre Instabilitäten erfassen (Knicken und Beulen).

C 3.1.5 Werkstoffverhalten

In den meisten Fällen wird lineares Werkstoffverhalten (lineare Spannungs-Dehnungs-Beziehung), gegebenenfalls unter Berücksichtigung der Temperaturabhängigkeit der Konstanten, und unter Berücksichtigung von Anfangsdehnungen angenommen.

Die Berücksichtigung nichtlinearen Werkstoffverhaltens (z.B. starrplastisch, linear elastisch - ideal plastisch, allgemein elastoplastisch, viskoelastisch) ist meist mit größerem Aufwand möglich.

C 3.2 Grundlagen der FEM

C 3.2.1 Vorbemerkung

Die Grundzüge der FEM werden hier insoweit erläutert, als sie für die Anwendung der FEM und die Beurteilung der Rechenergebnisse wesentlich sind. Diese Erläuterungen dienen auch der Bestimmung der hier verwendeten Begriffe.

Wie jedem thermomechanischen Berechnungsverfahren liegen auch der FEM die physikalischen Prinzipien der Kontinuumsmechanik zugrunde. Diese Prinzipien werden bei der FEM je nach Wahl der Diskretisierungsmethode auf verschiedene Weise exakt oder näherungsweise erfüllt.

C 3.2.2 Grundlegende Begriffe und physikalische Prinzipien

C 3.2.2.1 Felder

C 3.2.2.2 Kinematische Beziehungen

Dort wo sich ein Tragwerk als Kontinuum verhält, ist das Verschiebungsfeld in seinem Innern zu jedem Zeitpunkt stetig. Durch kinematische Randbedingungen werden Werte für Verschiebungsgrößen an Rändern des Berechnungsgebiets vorgeschrieben. Erfüllt ein Verschiebungsfeld sowohl die Stetigkeitsforderung als auch die kinematischen Randbedingungen, so bezeichnet man es als kinematisch verträglich (kinematisch zulässig).

Die Stetigkeit des Verschiebungsfeldes bedeutet bei Tragwerken, deren Deformation nur durch die Verschiebungsgrößen einer Fläche oder einer Linie beschrieben wird (Platten und Schalen bzw. Balken), auch, dass an jedem Punkt der Bezugsfläche oder -linie nicht nur die Verschiebungen, sondern auch die Verdrehungen um zwei in der Fläche oder drei im Raum liegende Achsen stetig sind.

Beispiele für kinematische Randbedingungen:

starre Einspannung,
starre Auflager,
vorgeschriebene Randverschiebungsgrößen.

Bei gleitenden Lagerungen ist die Bedingung der Null-Verschiebung senkrecht zur Gleitfläche kinematisch, bei gelenkigen Lagerungen die Bedingung der Null-Verschiebung der Gelenke (nicht jedoch die Bedingung der Spannungs- oder Kräftefreiheit).

Die Deformation in der unmittelbaren Umgebung eines Punktes des Tragwerkes wird durch die Verzerrungen (Längenänderung eines Linienelements, Winkeländerung zwischen zwei Linienelementen) beschrieben.

Die Voraussetzung für einen linearen Zusammenhang zwischen den Verschiebungen und den Verzerrungen sind kleine Verzerrungen und Verdrehungen, wobei die Größenordnung der Verdrehungen höchstens gleich der Größenordnung der Verzerrungsquadrate ist. Sind diese Voraussetzungen gegeben, so liegt geometrische Linearität vor.

C 3.2.2.3 Erhaltungssätze und Gleichgewichtsbedingungen

Für einen Teil oder die Gesamtheit des Tragwerkes sind zu jedem Zeitpunkt der Impuls- und der Impulsmomentsatz sowie statische Randbedingungen erfüllt. Für quasistationäre mechanische Vorgänge führt dies auf die inneren Gleichgewichtsbedingungen:

Summe der Kräfte am (deformierten) Volumenelement ist gleich Null,
Summe der Momente am (deformierten) Volumenelement ist gleich Null.

Randbedingungen, die Werte für Kraftgrößen vorschreiben, werden statische Randbedingungen genannt. Beispiele für statische Randbemerkungen:

Rand belastet durch Flächenlast, Linienlast oder Punktlast,
lastfreier Rand ohne sonstige Bedingungen,
Bedingung für Reibungskräfte in gleitenden Lagern,
Bedingung für Momentenfreiheit eines gelenkigen Auflagers.

An allen Punkten mit statischen Randbedingungen stehen die inneren Spannungen und Kräfte mit den angreifenden äußeren Belastungen (die Null sein können) im Gleichgewicht.

Die Gleichgewichtsbedingungen sind gleichwertig mit dem Prinzip der virtuellen Arbeit; dieses lässt sich folgendermaßen formulieren:

Diese Bedingung stellt unter Einbeziehung der Impulssätze den Zusammenhang zwischen der zeitlichen Änderung der Temperatur im Element und den räumlichen Ableitungen der Wärmeflüsse her.

Die differentielle Formulierung der Erhaltungssätze führt auf im Allgemeinen partielle Differentialgleichungen für die den momentanen Zustand des physikalischen Systems beschreibenden Feldgrößen (z.B. Verschiebungen, Verschiebungsgeschwindigkeit, Temperatur).

C 3.2.2.4 Materialgesetze

Für das mechanische Verhalten eines Festkörpers gibt das Materialgesetz den Zusammenhang zwischen Spannungen und Verzerrungen an. Bei linearelastischem Materialverhalten ist dieser Zusammenhang linear, während z.B. bei elastoplastischem Verhalten das Materialgesetz nichtlinear ist. Bei linearelastischen, isotropen Stoffen lässt sich das Materialverhalten mit zwei voneinander unabhängigen Koeffizienten beschreiben. Bei linearelastischen, anisotropen Stoffen können bis zu 21 voneinander unabhängige Koeffizienten erforderlich werden.

Das Materialgesetz für ein Fluid liefert einen Zusammenhang zwischen den Zustandsgrößen, z.B. für ein ideales Gas zwischen Druck, Dichte und Temperatur (thermische Zustandsgleichung).

Zusätzliche Parameter sind erforderlich bei thermischer Belastung (z.B. Wärmeausdehnungszahl, Wärmeleitzahl, temperaturabhängige E-Moduln) und bei strömenden Medien (z.B. Wärmeübergangszahl, Viskosität).

C 3.2.3 Diskretisierung

C 3.2.3.1 Vorgehensweise

Die Darstellung des Tragwerkes als Rechenmodell wird als Idealisierung bezeichnet. Nach der FEM wird das zu untersuchende Tragwerk in eine Anzahl von relativ einfachen Bereichen, den finiten Elementen, aufgeteilt (Diskretisierung). Jedes finite Element beinhaltet einen Ansatz für die Felder. Durch Anwendung eines Integralprinzips werden die verschiedenen Ansatzfunktionen so aufeinander abgestimmt, dass eine möglichst genaue Lösung erhalten wird. Je nach Ansatz und Integralprinzip werden mehrere Methoden unterschieden. In den Abschnitten C 3.2.3, C 3.3.1 und C 3.3.3 wird nur die Verschiebungsmethode betrachtet.

Bei der Verschiebungsmethode bezieht sich der Ansatz auf Verschiebungsformen innerhalb der finiten Elemente. Jedem Elemententyp liegt ein bestimmter Verschiebungsansatz und eine bestimmte Elementgestalt zugrunde. Beispiel: dreieckiges Scheibenelement mit sechs Knotenpunkten, den drei Eckpunkten und den drei Seitenmittelpunkten.

Im Hinblick auf die Möglichkeit der Fehlerabschätzung sollte der Verschiebungsansatz der einzelnen Elemente folgende Forderungen erfüllen:

kinematische Verträglichkeit innerhalb des Elementes und über die Grenzen der Elemente hinweg; letzteres wird durch passende Zuordnung von Verschiebungsverteilungen zu diskreten Freiheitsgraden, den Knotenpunktverschiebungen, erreicht,
die Verschiebungsformen sollen jede mögliche starre Verschiebung oder Verdrehung eines Elementes exakt beschreiben, und die aus solchen Verschiebungen abgeleiteten Verzerrungen sollen identisch Null sein.

Es wird nun angenommen, dass sich die Spannungen über das Materialgesetz aus den Verzerrungen berechnen lassen, die ihrerseits aus den Verschiebungsansätzen abgeleitet werden. So kann der obenerwähnte Elementtyp wegen des quadratischen Verschiebungsansatzes einen linearen Verlauf der Verzerrungen und somit bei linearem Materialgesetz auch einen linearen Verlauf der Spannungen beschreiben: bei linearem Verschiebungsansatz wäre in diesem Beispiel die Spannung konstant innerhalb eines Elements.

Durch Anwendung des Prinzips der virtuellen Arbeit bestimmt man diejenige Näherungslösung, deren äußere und innere virtuellen Arbeiten den exakten Werten möglichst nahe kommen. Dazu werden kinematische (wesentliche) Randbedingungen exakt erfüllt. Die statischen (natürlichen) Randbedingungen und inneren Belastungen werden kinematisch konsistent (kinematisch äquivalent) erfasst, d. h. die entsprechenden Knotenpunktskräfte werden aus den tatsächlichen Lasten so errechnet, dass mit Bezug auf die gewählten Verschiebungsformen die virtuellen Arbeiten der tatsächlichen Lasten und der Knotenpunktskräfte gleich sind.

C 3.2.3.2 Eigenschaften der Lösung

Die so errechnete Lösung stellt in zweierlei Hinsicht eine Näherungslösung dar:

Physikalische Diskretisierung
Wegen der Beschränkung der möglichen Freiheitsgrade durch die Wahl bestimmter finiter Elemente können die örtlichen Gleichgewichts- und statischen Randbedingungen im Allgemeinen nicht exakt erfüllt sein. Werden beide in Abschnitt C 3.2.3.1 erwähnten Bedingungen für die Verschiebungsansätze in den Elementen gehalten, und sieht man zunächst von numerischen Einflüssen ab, so stellt die errechnete Lösung für die getroffene Wahl der Elemente die beste Näherung in dem Sinne dar, dass die virtuellen Arbeiten (und deshalb das Gleichgewicht im großen) möglichst genau erfasst werden; für die den Freiheitsgraden zugeordneten Knotenpunktskraftgrößen ist das Gleichgewicht exakt erfüllt, sofern die Verschiebungssätze alle Starrkörper-Verschiebungen und -Verdrehungen enthalten. Die errechnete Lösung gibt das Tragwerksverhalten als zu steif wieder. Für eine gegebene Belastung ist die errechnete Verschiebung also eher zu klein; die errechneten Eigenschwingungsfrequenzen stellen obere Schranken dar.

Werden Elemente gewählt, die nicht vollständig verträglich sind, so besteht keine Gefahr mehr, dass die errechnete Lösung eine bestmögliche Näherung im oben erläuterten Sinn darstellt. Die Verletzung der kinematischen Verträglichkeit wirkt allerdings der Überschätzung der Steifheit entgegen, und die so errechnete Lösung kann in gewissen Fällen, insbesondere für die Verschiebungen, genauere Ergebnisse liefern als ein voll verträgliches Modell; die so gefundene Lösung besitzt allerdings nicht mehr die oben erwähnten Schrankeneigenschaften.

Beispiel für nicht vollständig verträgliche Elemente: Werden ebene Scheiben- und Plattenelemente mit verschiedenen Ansätzen für die Verschiebungskomponenten in der Elementebene und senkrecht dazu über Knicke miteinander verbunden, so wird die kinematische Verträglichkeit an diesen Knicken verletzt.

Weicht die Gestalt der durch finite Elemente idealisierten Struktur von der tatsächlichen Tragwerksgestalt merklich ab, so können hierdurch Ungenauigkeiten entstehen. In vielen Fällen ändert die Annäherung gekrümmter Konturen durch stückweise gerade oder ebene Elemente zwar das gesamte Deformationsverhalten nur unwesentlich, doch können die örtlichen Verschiebungs- und insbesondere Verzerrungs- und Spannungskomponenten an solchen künstlichen Knickstellen nur schwer interpretiert werden.
Numerische Approximation
Für eine gegebene physikalische Diskretisierung weicht die numerische Lösung von der exakten ab. Diese Abweichung hat zwei Ursachen:
- Wegen der beschränkten Stellenzahl in der Datenverarbeitungsanlage entstehen Anfangsabbrechfehler und Rundungsfehler. Dies kann sich besonders bei Systemen mit extrem unterschiedlichen physikalischen Eigenschaften im Rechenmodell auswirken.
  Durch die Berechnung von Konditionszahlen, die eine Abschätzung der Vergrößerung des Anfangsabbrechfehlers durch die Rundungsfehler gestatten, kann man eine untere, oft sehr konservative Schranke für die Zahl der numerisch exakten Stellen bekommen.
  
  Erfassen die verwendeten Elemente Verschiebungen und Verdrehungen des Starrkörpers exakt (die zweite der Forderungen von Abschnitt C 3.2.3.1 bezüglich des Elementansatzes), so stellt die genaue Erfüllung des Gleichgewichts der Knotenkräfte eine notwendige, allerdings nicht hinreichende Bedingung für die Genauigkeit der numerischen Lösung bei statischen Problemen dar.
- Bei bestimmten Algorithmen, z.B. der iterativen Gleichungsauflösung oder der iterativen Lösung des Eigenwertproblems, verbleibt ein Fehler, der von einer vorgegebenen Genauigkeitsschranke abhängt.

C 3.3 Anwendung der FEM

C 3.3.1 Idealisierung der Geometrie und Belastung

C 3.3.1.1 Umfang der Idealisierung

Mechanische Probleme können sowohl global als auch im Detail berechnet werden. Die Anforderungen an die Ergebnisse bestimmen den Aufwand der Idealisierung. Durch die Auswahl von geeigneten Elementtypen, Festlegung von Knotenpunkten und Formulierung der Randbedingungen wird die Qualität der Näherung entscheidend beeinflusst.

C 3.3.1.2 Auswahl der Elementtypen

Die Elemente sind im Hinblick auf die Aufgabenstellung auszuwählen. Folgende Gesichtspunkte müssen hierbei beachtet werden:

problemgerechte Abbildung der Geometrie,
Eignung des Elementansatzes für die problembedingten statischen und kinematischen Randbedingungen (z.B. Lasteinleitung, Lastverteilung, Lagerung),
Art und Genauigkeit der Ergebnisse entsprechend der Aufgabenstellung.

C 3.3.1.3 Festlegung von Lage und Anzahl der Knotenpunkte

Lage und Anzahl der Knotenpunkte sollen so gewählt werden, dass das Rechenergebnis für die jeweilige Aufgabenstellung genügend genau ist, wobei die Gesichtspunkte von Abschnitt C 3.3.1.2 sinngemäß zu berücksichtigen sind. Außerdem ist folgendes zu beachten:

Erfordert die Aufgabenstellung der Berechnung die Kenntnis stark veränderlicher Feldkomponenten, z.B. Verformungen oder Spannungen, so ist die Feinheit des Netzes entsprechend zu wählen.
An den Grenzen zwischen maßgebend verschiedenen Materialeigenschaften sollen möglichst auch Elementgrenzen liegen, falls nicht eine inhomogene Verteilung der Materialeigenschaften innerhalb eines Elementes berücksichtigt werden kann.
Es ist in Abhängigkeit vom gewählten Elementtyp der Einfluss der Seitenverhältnisse auf die Konditionierung des Systems zu berücksichtigen. Auch sollen im Allgemeinen benachbarte Elemente gleiche Größenordnungen von Geometrie und Steifigkeit aufweisen, d. h. Übergänge von großen zu kleinen oder steifen zu weniger steifen Elementen sollen allmählich verlaufen, da sich starke Unterschiede in der Steifigkeit von Element zu Element in einer Verschlechterung der Konditionierung der Gleichungsmatrix auswirken.
Das Netz muss eine im Rahmen der Aufgabenstellung hinreichend genaue Abbildung der eingeprägten Kräfte und sonstiger Belastungen und Randbedingungen ermöglichen.
Für dynamische Probleme muss das Netz so gestaltet werden, dass das dynamische Verhalten der Struktur der Berechnung zugänglich wird. Zahl und Art der Freiheitsgrade müssen so gewählt werden, dass die interessierenden Bewegungsformen beschrieben werden können. Dies gilt besonders für die Kompensation der dynamischen Freiheitsgrade.
Die Idealisierung der Struktur soll so erfolgen, dass keine lokalen oder globalen Singularitäten der Steifigkeitsmatrix auftreten. Andernfalls müssen diese im Lösungsalgorithmus berücksichtigt werden. Die Behandlung lokaler Fast-Singularitäten (nach Maßgabe der Konditionierung und Rechengenauigkeit) darf nicht zur Verfälschung des physikalischen Verhaltens der Struktur führen. Bei Fast-Singularitäten ist besonders auf hinreichende numerische Genauigkeit der Ergebnisse zu achten.

C 3.3.1.4 Formulierung der Randbedingungen

C 3.3.1.4.1 Arten von Randbedingungen

Die Randbedingungen können Bedingungen für äußere Kraft- und Verschiebungsgrößen umfassen, sie können aber auch aus Schnittbedingungen an gedachten Schnitträndern bestehen, z.B. Detailuntersuchungen, Symmetriebedingungen. Durch letzte darf die Dehnungs- und Spannungsverteilung des Bauteils nicht verfälscht werden.

Lastveränderlichen Randbedingungen ist besondere Beachtung zu schenken.

C 3.3.1.4.2 Kinematische Randbedingungen

Kinematische Randbedingungen sind direkt in den Freiheitsgraden zu formulieren. Bei Einsatz von Elementen, die nicht voll kinematisch verträglich sind, ist auf hinreichende Beschreibung dieser Randbedingungen zu achten.

C 3.3.1.4.3 Statische Randbedingungen

Die in den Knotenpunktskraftgrößen gegebenen statischen Randbedingungen sind direkt als Knotenpunktsbelastungen einzusetzen. Nicht an den Knotenpunkten angreifende Punktlasten sowie Flächen- und Volumenlasten müssen auf kinematisch äquivalente Knotenpunktskraftgrößen umgerechnet werden. Bei Verwendung von Elementtypen, deren Verschiebungsansatz hinsichtlich starrer Verschiebungen und Verdrehungen unvollständig ist, muss dabei auch auf Einhaltung der statischen Äquivalenz geachtet werden.

C 3.3.1.5 Festlegung der Last- oder Zeitinkremente

Die Last- oder Zeitinkremente sind so zu wählen, dass der Verlauf der Verschiebungen und der aus ihnen abgeleiteten Größen über dem Lastparameter oder über der Zeit für die jeweilige Aufgabenstellung genügend genau erfasst wird, und dass die numerische Stabilität der Lösungen gewährleistet ist. Bei Material-Nichtlinearitäten ist zudem auf genügend genaue Erfüllung des Materialgesetzes, bei geometrischen Nichtlinearitäten auf die Gleichgewichtsbedingungen zu achten.

C 3.3.1.6 Kontrolle der Eingabedaten

Wegen der normalerweise großen Menge der Eingabedaten ist eine Kontrolle unerlässlich. Diese sollte möglichst anhand der programmierten gespeicherten Daten durchgeführt werden.

Routinen zur Prüfung der Eingabedaten sowie graphische Darstellung der Eingabedaten, z.B. der Geometrie, der Randbedingungen und der Belastungen, sind zweckmäßig.

C 3.3.2 Programme

C 3.3.2.1 Allgemeines

Rechnungen nach der FEM werden wegen der damit verbundenen hohen Anzahl von Rechenoperationen nur mit Programmen auf Datenverarbeitungsanlagen durchgeführt.

C 3.3.2.2 Dokumentation der Programme

Zu jedem verwendeten Programm muss eine Dokumentation vorliegen. Darin müssen folgende Punkte beschrieben oder angegeben sein:

Kennzeichnung des Programms, einschließlich Änderungszustand,
theoretische Grundlagen,
Anwendungsbereich und Voraussetzungen,
Beschreibung der Programmorganisation, soweit für die Benutzung und Beurteilung erforderlich,
Eingabevorschriften zur Programmsteuerung und Problembeschreibung,
Erläuterung der Ausgabe,
Anwendungsbeispiele.

Im Teil Anwendungsbeispiele müssen demonstrative und überprüfte Berechnungsbeispiele für die Anwendung enthalten sein.

C 3.3.2.3 Zuverlässigkeit der Programme

Wegen des Umfangs der FEM-Programme kann die Fehlerfreiheit nicht ohne weiteres für alle möglichen Rechenwege vorausgesetzt werden. Deshalb sind zur Beurteilung der Zuverlässigkeit folgende Gesichtspunkte zu berücksichtigen:

modularer Aufbau des Programms,
standardisierte Programmsprache,
zentrale Programmwartung,
großer Benutzerkreis und häufiger Programmeinsatz, insbesondere für den vorliegenden Anwendungsbereich.

Das zuverlässige Arbeiten des Programms kann in dem Maß erwartet werden, in dem die genannten Gesichtspunkte für die jeweilige Programmversion erfüllt sind.

C 3.3.3 Beurteilung von Rechenergebnissen

C 3.3.3.1 Allgemeines

Der erste Schritt bei der Beurteilung von Rechenergebnissen ist stets die Prüfung, ob die Ergebnisse physikalisch einleuchtend sind. Diese Prüfung ist umso aussagekräftiger, je besser die Gesamtheit der Ergebnisse zu überblicken ist. Die Plausibilität der Ergebnisse stellt eine notwendige Bedingung für deren Brauchbarkeit dar. Zusätzlich sind die Eignung des Rechenmodells, die Richtigkeit der Daten und die einwandfreie Arbeitsweise und Anwendung des Programms zu überprüfen.

Da jede mit diskretisierenden numerischen Verfahren erhaltende Lösung eine Näherung des physikalischen Verhaltens darstellt, ist zu prüfen, ob die Güte der Näherung für das gestellte Problem ausreicht. Sofern die Gültigkeit der Diskretisierung der Struktur und die Gültigkeit der numerischen Lösung durch diese Kontrollen nachgewiesen werden sollen, so können diese in dem Umfang entfallen, in dem sie bereits bei direkt vergleichbaren anderen Rechnungen durchgeführt wurden; als direkt vergleichbar können Probleme angesehen werden, bei denen vergleichbare Strukturen unter qualitativ gleichen Belastungen idealisiert wurden und bei denen alle Parameter, die die Berechnung charakterisieren, ungefähr übereinstimmen.

C 3.3.3.2 Physikalische Kontrolle

Bei der Verschiebungs-FEM werden exakt erfüllte und angenähert erfüllte physikalische Bedingungen unterschieden. Daher können für die Kontrolle der errechneten Lösung die folgenden Kriterien angegeben werden.

Bei Verwendung von kinematisch verträglichen Elementen werden die örtlichen Gleichgewichtsbedingungen im Innern und am Rand durch die Methode näherungsweise erfüllt. Die Kriterien für die Güte der Näherung sind:

Größe der Unstetigkeiten in den elementweise errechneten Spannungskomponenten benachbarter Elemente,
Übereinstimmung entsprechender Spannungskomponenten mit angreifender verteilter Belastung an belasteten oder freien Rändern.

Werden nichtverträgliche Elemente eingesetzt, so ist zudem die Genauigkeit der Erfüllung der inneren kinematischen Verträglichkeitsbedingungen zu überprüfen. Da bei nichtverträglichen Elementen die Verträglichkeit meist nur an den Knotenpunkten erfüllt ist, muss in solchen Fällen die Elementeinteilung entsprechend fein gewählt werden.

Die Genauigkeit der Erfüllung des Gleichgewichts der Knotenpunktskraftgrößen ist für folgende Fälle zu überprüfen:

bei Verwendung von Elementen, die die in Abschnitt C 3.2.3.1 angeführte Bedingung hinsichtlich der Starrkörper-Verschiebungsformen nicht erfüllen,
bei örtlichen Singularitäten, Fast-Singularitäten oder künstlichen Auflagern infolge Unterdrückung fastsingulärer Freiheitsgrade,
bei allen nichtlinearen Problemen.

Bei Problemen mit nichtlinearem Materialverhalten ist zudem die Erfüllung des Materialgesetzes zu überprüfen.

C 3.3.3.3 Numerische Kontrolle

C 3.3.3.3.1 Vorbemerkung

Grundsätzlich wird durch eine feinere Unterteilung der zu untersuchenden Struktur der Fehler infolge der physikalischen Diskretisierung verringert, die Anfälligkeit für numerische Fehler im Allgemeinen erhöht.

C 3.3.3.3.2 Untersuchung des Lösungsvektors

Einsetzen der Komponenten des Lösungsvektors in das ursprüngliche Gleichungssystem gibt Auskunft über die Größenordnung des numerischen Fehlers. Bei statischen Problemen stellt die Bedingung nach ausreichender Erfüllung des Gleichgewichts der Knotenpunktskraftgrößen eine notwendige (aber nicht hinreichende) Bedingung für ausreichende numerische Genauigkeit der Verschiebungsgrößen dar.

C 3.3.3.3.3 Kontrolle mittels Konditionszahlen

C 3.3.3.4 Vergleich mit Ergebnissen aus anderen Untersuchungen

C 3.3.3.4.1 Allgemeines

Zur Beurteilung der Ergebnisse von Rechnungen nach der FEM können als Ergänzung oder als Ersatz der Kontrollen gemäß den Abschnitten C 3.3.1.6, C 3.3.2.3, C 3.3.3.1, C 3.3.3.2 und C 3.3.3.3 herangezogen werden:

Vergleiche mit anderen FEM-Rechnungen,
Vergleiche mit Rechnungen nach anderen Berechnungsverfahren und
Vergleiche mit experimentell ermittelten Ergebnissen.

Die Wahl des für den Vergleich zu verwendenden Untersuchungsverfahrens ist in Abhängigkeit davon zu treffen, wo der Schwerpunkt der Kontrolle liegen soll (theoretische Formulierung, Programmierung, Diskretisierung, Eingabedaten und numerische Genauigkeit).

C 3.3.3.4.2 Vergleich mit anderen FEM-Rechnungen

Durch den Vergleich der Ergebnisse einer Rechnung nach der FEM mit Ergebnissen anderer Rechnungen nach der FEM können in Abhängigkeit vom benutzten Programm und von der gewählten Idealisierung einzelne oder alle Eigenschaften der FEM-Lösungen beurteilt werden.

Für die Vergleichsrechnung ergibt sich die Möglichkeit der Benutzung gleicher oder verschiedener Programme, Betriebssysteme, Datenverarbeitungsanlagen sowie gleicher oder verschiedener Idealisierungen.

Bei der Überprüfung der Programmzuverlässigkeit durch Vergleichsrechnungen ist ein unabhängiges Programm und dieselbe Idealisierung zu verwenden.

Die numerische Genauigkeit kann verbessert werden, wenn die Stellenzahl entsprechend erhöht wird.

Die Gültigkeit der Idealisierung kann durch Vergleichsrechnung mit anderen Idealisierungen überprüft werden.

Vergleichsrechnungen mit gleichen oder verschiedenen Programmen und gleichen Idealisierungen dienen der Kontrolle der Eingabedaten, wenn diese unabhängig erstellt wurden.

C 3.3.3.4.3 Vergleich mit Rechnungen nach anderen Berechnungsverfahren

Soweit andere Berechnungsverfahren, z.B. die FDM oder SKM die Voraussetzungen zur Behandlung des jeweils vorliegenden Problems bieten, können sie zu Vergleichsrechnungen herangezogen werden. Diese Vergleichsrechnungen dienen dann zur globalen Beurteilung aller Eigenschaften der FEM-Lösungen.

C 3.3.3.4.4 Vergleich mit experimentell ermittelten Ergebnissen

Die Beurteilung der Ergebnisse von Rechnungen nach der Methode der finiten Elemente kann teilweise oder vollständig durch den Vergleich mit experimentell ermittelten Werten erfolgen, wobei die Eigenarten und Grenzen der Messverfahren zu berücksichtigen sind. Die Messergebnisse können aus Messungen am Modell (z.B. aus spannungsoptischen Untersuchungen) oder aus Messungen am Bauteil (Dehnungs- oder Verschiebungsmessungen) gewonnen werden, soweit alle wesentlichen Parameter simuliert werden können. Bei Verwendung von Modellen müssen diese für das gestellte Problem repräsentativ sein. Dieser Vergleich dient insbesondere der Beurteilung der Zuverlässigkeit der physikalischen Annahmen, die der Idealisierung zugrunde liegen.

Verfahren zur Sprödbruchanalyse

Anhang D

D 1 Konstruktion des modifizierten Porsediagramms mit Beispiel

(1) Mit der nach KTA 3201.1 ermittelten Referenztemperatur RTNDT und dem von Pellini aufgestellten qualitativen Zusammenhang zwischen kritischer Risslänge und Spannung lässt sich das in Bild D 1-1 dargestellte Diagramm für den unbestrahlten Zustand und analog für den bestrahlten Zustand zeichnen. Nach Pellini ist bei beliebiger Risslänge oberhalb der Rissstopptemperatur TDT kein Sprödbruch zu erwarten. Diese Aussage ergibt im Diagramm die senkrechte Linie.

Die untere Begrenzung des Diagramms ergibt sich aus einem modifizierten Ansatz von Porse.

Das Sprödbruchdiagramm für den bestrahlten Zustand darf unter denselben Bedingungen gezeichnet werden, wobei die justierte Referenztemperatur RTNDT verwendet werden muss (siehe KTA 3203).

In Bild D 1-1 ist neben dem Sprödbruchdiagramm als charakteristisches Beispiel ein Fahrdiagramm (Spannung als Funktion der Temperatur) eingetragen. Dieses Fahrdiagramm gibt den Zusammenhang zwischen Temperatur und Beanspruchung in der zylindrischen Behälterwand wieder. In der Beanspruchung sind die Spannungen durch den Innendruck und die instationären Wärmespannungen an der durch Membranspannung höchstbeanspruchten Stelle des Reaktordruckbehälters berücksichtigt. Das Fahrdiagramm muss stets außerhalb des vom Porsediagramm gekennzeichneten Bereichs liegen.

(2) Konstruktion des modifizierten Porsediagramms Ausgangsdaten:

Streckgrenze R_p0,2bei T = 20 °C

RT_NDT-Temperatur: ΔT_NDT= ΔT₄₁

unbestrahlt:

Punkt 1	T = (RT_NDT+ 33 K) - 110 K σ = 0, 1 - R_p0,2
Punkt 2	T = RT_NDT σ = 0,2 - R_p0,2
Punkt 3	Schnittpunkt von T = RT_NDT+ 33 K mit der Verlängerung der Geraden 1-2;
Punkt 4	T = RT_NDT+ 33 K σ = 1,0 - R_p0,2

bestrahlt:

Punkt 1´	T = (RT_NDT+ 33 K) 110 K + ΔT_NDT σ = 0, 1 - R_p0,2
Punkt 2´	T = RT_NDT+ ΔT_NDT σ = 0,2 - R_p0,2
Punkt 3´	Schnittpunkt von T = RT_NDT+ 33 K + ΔT_NDTmit der Verlängerung der Geraden 1- 2´;
Punkt 4´	T = RT_NDT + 33 K + ΔT_NDT σ = 1,0 - R_p0,2

Bild D 1-1: Sprödbruchübergangstemperaturkonzept und modifiziertes Porsediagramm (Beispiel)

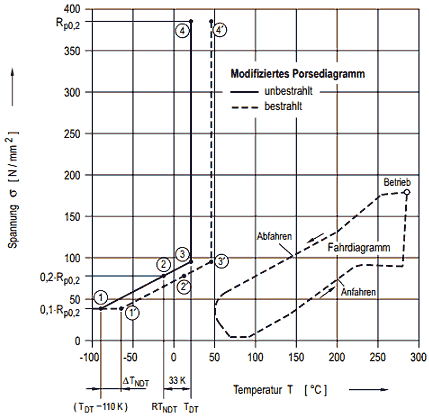
D 2 Ermittlung der Bruchzähigkeit nach Warmvorbelastung

(1) Nach Warmvorbelastung der Rissfront und bei monoton abnehmendem Spannungsintensitätsfaktor, d. h. bei dK/dtd 0, ist Rissinitiierung ausgeschlossen. Die Warmvorbelastung bewirkt außerdem eine Erhöhung der Bruchzähigkeit über K_Icauf K_FRAC. Damit ist Rissinitiierung auch bei erneuten Anstieg des Spannungsintensitätsfaktors nach Warmvorbelastung ausgeschlossen, wenn der Spannungsintensitätsfaktor die Bruchzähigkeit K_FRACnicht erreicht. Bild D 2-1 zeigt in einer Prinzipdarstellung, dass die Bruchzähigkeit nach Warmvorbelastung von der Entlastung vor einem erneuten Anstieg des Spannungsintensitätsfaktors abhängig ist.

(2) Für die Ermittlung der Bruchzähigkeit dürfen

die Gleichung (D 2-1) bei Teilentlastung vor erneuter Belastung (LPUCF-Pfad),
die Gleichung (D 2-2) ohne Entlastung vor erneuter Belastung (LCF-Pfad),
die Gleichung (D 2-3) bei vollständiger Entlastung vor erneuter Belastung (LUCF-Pfad)

oder andere geeignete Verfahren angewendet werden.

Hinweis:
Andere geeignete Verfahren hierfür sind z.B. in BS 7910:1999, Annex O angegeben.

Die in den Gleichungen verwendeten Formelzeichen bedeuten:

K_WPS	: Spannungsintensitätsfaktor bei Warmvorbelastung
K_Unl	: Spannungsintensitätsfaktor bei Entlastung
K_Ic	: Bruchzähigkeit bei Wiederbelastungstemperatur
K_FRAC	: Bruchzähigkeit bei Wiederbelastungstemperatur nach Warmvorbelastung
R_eWPS	: Streckgrenze bei Warmvorbelastung
R_eFRAC	: Streckgrenze bei Wiederbelastung

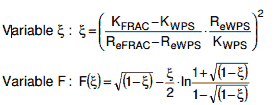
Bild D 2-1: Prinzipdarstellung zur Ermittlung der Bruchzähigkeit KFRAC nach Warmvorbelastung

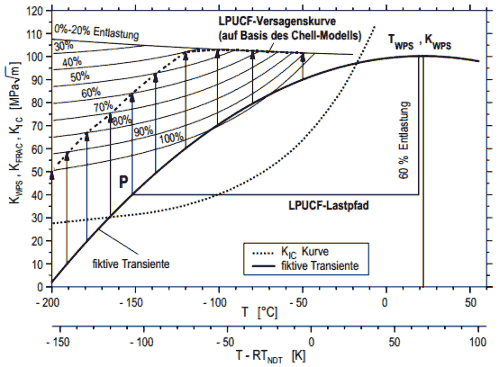
LCF:	Warmvorbelastung-Abkühlung-Wiederbelastungsbruch (Load-Cool-Fracture)
LPUCF:	Warmvorbelastung-Teilentlastung-Abkühlung-Wiederbelastungsbruch (Load-Partial-Unload-Cool-Fracture)
LUCF:	Warmvorbelastung-Entlastung-Abkühlung-Wiederbelastungsbruch (Load-Unload-Cool-Fracture)

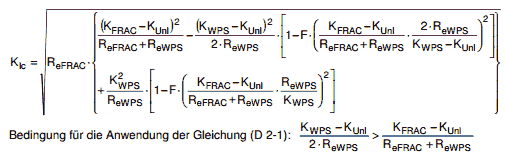	(D 2-1)
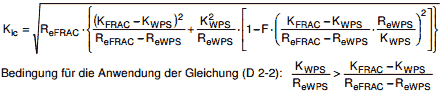	(D 2-2)
	(D 2-3)

Bestimmungen und Literatur, auf die in dieser Regel verwiesen wird

Anhang E

(Die Verweise beziehen sich nur auf die in diesem Anhang angegebene Fassung. Darin enthaltene Zitate von Bestimmungen beziehen sich jeweils auf die Fassung, die vorlag, als die verweisende Bestimmung aufgestellt oder ausgegeben wurde.)

AtG	Gesetz über die friedliche Verwendung der Kernenergie und den Schutz gegen ihre Gefahren (Atomgesetz - AtG) in der Fassung der Bekanntmachung vom 15. Juli 1985 (BGBl. I S. 1565), das zuletzt durch Artikel 5 des Gesetzes vom 28. August 2013 (BGBl. I S. 3313) geändert worden ist
StrlSchV	Verordnung über den Schutz vor Schäden durch ionisierende Strahlen (Strahlenschutzverordnung - StrlSchV) vom 20. Juli 2001 (BGBl. I 2001, Nr. 38, S. 1714), die zuletzt durch Artikel 5 Absatz 7 des Gesetzes vom 24. Februar 2012 (BGBl. I S. 212) geändert worden ist
Sicherheitskriterien	(1977-10)	Sicherheitskriterien für Kernkraftwerke vom 21. Oktober 1977 (BAnz. Nr. 206 vom 3. November 1977)
SiAnf	Sicherheitsanforderungen an Kernkraftwerke (SiAnf) vom 22. November 2012 (BAnz vom 24.01.2013)
Störfall-Leitlinien	(1983-10)	Leitlinien zur Beurteilung der Auslegung von Kernkraftwerken mit Druckwasserreaktoren gegen Störfälle im Sinne des § 28 Abs. 3 StrlSchV (Störfall-Leitlinien) vom 18. Oktober 1983 (Beilage zum BAnz. Nr. 245 vom 31. Dezember 1983)
KTA 1404	(2013-11)	Dokumentation beim Bau und Betrieb von Kernkraftwerken
KTA 2201.4	(2012-11)	Auslegung von Kernkraftwerken gegen seismische Einwirkungen; Teil 4: Anlagenteile
KTA 3201.1	(1998-06)	Komponenten des Primärkreises von Leichtwasserreaktoren; Teil 1: Werkstoffe und Erzeugnisformen
KTA 3201.3	(2007-11)	Komponenten des Primärkreises von Leichtwasserreaktoren; Teil 3: Herstellung
KTA 3201.4	(2010-11)	Komponenten des Primärkreises von Leichtwasserreaktoren; Teil 4: Wiederkehrende Prüfungen und Betriebsüberwachung
KTA 3203	(2001-06)	Überwachung des Bestrahlungsverhaltens von Werkstoffen der Reaktordruckbehälter von Leichtwasserreaktoren
KTA 3205.1	(2002-06)	Komponentenstützkonstruktionen mit nichtintegralen Anschlüssen; Teil 1: Komponentenstützkonstruktionen mit nichtintegralen Anschlüssen für Primärkreiskomponenten in Leichtwasserreaktoren
DIN 267-13	(2007-05)	Mechanische Verbindungselemente - Technische Lieferbedingungen - Teil 13: Teile für Schraubenverbindungen mit besonderen mechanischen Eigenschaften zum Einsatz bei Temperaturen von -200 IC bis +700 IC
DIN EN ISO 898-1	(2013-05)	Mechanische Eigenschaften von Verbindungselementen aus Kohlenstoffstahl und legiertem Stahl - Teil 1: Schrauben mit festgelegten Festigkeitsklassen - Regelgewinde und Feingewinde (ISO 898-1:2013); Deutsche Fassung EN ISO 898-1:2013
DIN EN ISO 898-2	(2012-08)	Mechanische Eigenschaften von Verbindungselementen aus Kohlenstoffstahl und legiertem Stahl - Teil 2: Muttern mit festgelegten Festigkeitsklassen - Regelgewinde und Feingewinde (ISO 898-2:2012); Deutsche Fassung EN ISO 898-2:2012
DIN 2510-1	(1974-09)	Schraubverbindungen mit Dehnschaft; Übersicht, Anwendungsbereich und Einbaubeispiele
DIN 2510-2	(1971-08)	Schraubverbindungen mit Dehnschaft; Metrisches Gewinde mit großem Spiel, Nennmaße und Grenzmaße
DIN 2510-3	(1971-08)	Schraubenverbindungen mit Dehnschaft; Schraubenbolzen
DIN 2510-4	(1971-08)	Schraubenverbindungen mit Dehnschaft; Stiftschrauben
DIN EN ISO 3506-1	(2010-04)	Mechanische Eigenschaften von Verbindungselementen aus nichtrostenden Stählen - Teil 1: Schrauben (ISO 3506-1:2009); Deutsche Fassung EN ISO 3506-1:2009
DIN EN ISO 3506-2	(2010-04)	Mechanische Eigenschaften von Verbindungselementen aus nichtrostenden Stählen - Teil 2: Muttern (ISO 3506-2:2009); Deutsche Fassung EN ISO 3506-2:2009
DIN EN ISO 3506-3	(2010-04)	Mechanische Eigenschaften von Verbindungselementen aus nichtrostenden Stählen - Teil 3: Gewindestifte und ähnliche nicht auf Zug beanspruchte Verbindungselemente (ISO 3506-3:2009); Deutsche Fassung EN ISO 3506-3:2009
DIN EN 10253-2	(2008-09)	Formstücke zum Einschweißen - Teil 2: Unlegierte und legierte ferritische Stähle mit besonderen Prüfanforderungen; Deutsche Fassung EN 10253-2:2007
DIN EN 10253-4	(2008-06)	Formstücke zum Einschweißen - Teil 4: Austenitische und austenitischferritische (Duplex-) Stähle mit besonderen Prüfanforderungen; Deutsche Fassung EN 10253-4:2008
DIN EN 12516-2	(2004-10)	Industriearmaturen - Gehäusefestigkeit - Teil 2: Berechnungsverfahren für drucktragende Gehäuse von Armaturen aus Stahl; Deutsche Fassung EN 12516-2:2004
DIN EN 13555	(2005-02)	Flansche und ihre Verbindungen - Dichtungskennwerte und Prüfverfahren für die Anwendung der Regeln für die Auslegung von Flanschverbindungen mit runden Flanschen und Dichtungen; Deutsche Fassung EN 13555:2004
DIN 28011	(2012-06)	Gewölbte Böden; Klöpperform
DIN 28013	(2012-06)	Gewölbte Böden; Korbbogenform
VDI 2230 Blatt 1	(2003-02)	Systematische Berechnung hochbeanspruchter Schraubenverbindungen - Zylindrische Einschraubenverbindungen
AD 2000-MB a 5	(2000-10)	Öffnungen, Verschlüsse und Verschlusselemente
ASTM E 1820	(2011)	Standard Test Method for Measurement of Fracture Toughness; Norm der "American Society for Testing and Materials"
ASTM E 1921-12	(2012)	Standard Test Method for Determination of Reference Temperature, T0, for Ferritic Steels in the Transition Range; Norm der "American Society for Testing and Materials"
ASME Code Case	Use of Fracture Toughness Test Data to Establish Reference Temperature for Pressure
N-629	Retaining Materials; Approval Date: 08/20/02
ASME Code Case	Use of Fracture Toughness Test Data to Establish Reference Temperature for Pressure
N-631	Retaining Materials, Other Than Bolting, Class 1 Vessels; Approval Date: 07/23/02
IAEa TRS 429	Guidelines for Application of the Master Curve Approach to Reactor Pressure Vessel Integrity in Nuclear Power Plants; Technical Reports Series No. 429, Vienna : International Atomic Energy Agency, 2005

Literatur

[1]	H. Hübel Erhöhungsfaktor Ke zur Ermittlung plastischer Dehnungen aus elastischer Berechnung, Technische Überwachung 35 (1994) Nr. 6, S. 268-278
[2]	WRC Bulletin 297 (September 1987) Local Stresses in Cylindrical Shells due to External Loadings on Nozzles-Supplement to WRC Bulletin No. 107 (Revision I)
[3]	WRC Bulletin 107 (August 1965, Revision März 1979) Local Stresses in Spherical and Cylindrical Shells due to External Loadings
[4]	British Standard PD 5500:2000, Annex G Specification for unfired Fusion welded Pressure Vessels
[5]	K. Bieniussa, H. Reck Rohrleitungsspezifische Analyse der Beanspruchungen aus thermischer Schichtung, 22. MPA-Seminar, 10. und 11. Oktober 1996, Stuttgart
[6]	Markus Theorie und Berechnung rotationssymmetrischer Bauwerke; 2. berichtigte Auflage, Düsseldorf 1976
[7]	Warren C. Young Roark´s Formulas for Stress and Strain, 6. Ausgabe, Verlag: McGraw-Hill, New York 1989
[8]	Kantorowitsch Die Festigkeit der Apparate und Maschinen für die chemische Industrie, Berlin 1955
[9]	Kockelmann, J. Bartonicek, E. G. Meyer, M. Trobitz Festigkeits- und Dichtheitsnachweis für Flanschverbindungen mit der Dichtung im Krafthaupt- und Kraftnebenschluss; Vortragsveranstaltung "Gewährleistung von Sicherheit und Verfügbarkeit von Leichtwasserreaktoren; 13.-14. Juni 2002, MPa Stuttgart
[10]	F. Schöckle, J. Bartonicek, R. Hahn, H. Kockelmann Abdichteigenschaften von Dichtungen für Flanschverbindungen; 28. MPA-Seminar, 10. und 11. Oktober 2002
[11]	R. Hahn, H. Kockelmann, J. Bartonicek, R. Jastrow, F. Schöckle Ermittlung von Kennwerten für Flanschverbindungen mit der Dichtung im Krafthaupt- und Kraftnebenschluss; 27. MPA-Seminar, 4. und 5. Oktober 2001, Stuttgart

Änderungen gegenüber der Fassung 1996-06 und Erläuterungen

Anhang F (informativ)

Zu Abschnitt 2 "Allgemeine Anforderungen und Begriffe"

Die Begriffsdefinitionen wurden in einem separaten Abschnitt zusammengefasst. Die zugehörigen Anforderungen wurden präzisiert.

Zu Abschnitt 3 "Lastfallklassen und Beanspruchungsstufen"

(1) Die Formulierungen zu den Beanspruchungsstufen wurden an mehreren Stellen präzisiert.

(2) In Abschnitt 3.3 wurden bei den Beanspruchungsstufen 0, A, B, C und D Hinweise ergänzt, in denen die Nachweisziele der jeweiligen Beanspruchungsstufen beschrieben sind.

(3) Der Abschnitt 3.3.3.2 wurde an die in den Tabellen 7.7-4 bis 7.7-6 vorgenommene Ergänzung von Primärspannungsbegrenzungen für die Stufe a angepasst.

(4) Die Festlegungen zur Berücksichtigung von Lastfällen der Stufe C in der Ermüdungsanalyse wurden in Abschnitt 3.3.3.4 und in den Tabellen 7.7-4 bis 7.7-6 präzisiert. Eine Berücksichtigung jedes aufgetretenen Lastspiels aus Ereignissen der Stufe C hinsichtlich seines Beitrags zur Bauteilermüdung erfolgt im Rahmen der Betriebsüberwachung (siehe KTA 3201.4 Abschnitt 9.1).

(5) Die Anforderung in Abschnitt 3.3.3.6 wurde derart geändert, dass alle Druckprüfungen in der Ermüdungsanalyse berücksichtigt werden müssen, sofern deren Anzahl die Zahl 10 überschreitet.

Zu Abschnitt 4 "Einwirkungen auf die Komponenten infolge von mechanischen und thermischen Belastungen, Einwirkungen des Mediums und Bestrahlung"

Es wurde neu aufgenommen, dass der Einfluss des Mediums auf die Bauteilermüdung entsprechend dem Stand von Wissenschaft und Technik zu berücksichtigen ist. Hierfür wurden folgende Änderungen vorgenommen:

An allen betreffenden Stellen wurde "Korrosion und Erosion" durch die allgemeinere Formulierung "Einwirkungen des Mediums" ersetzt.
In Absatz 3 wurde ergänzt, dass Einwirkungen des Mediums die Ermüdungsfestigkeit reduzieren können.
In Abschnitt 4.5 wurde ein neuer Absatz ergänzt, der in Verbindung mit den in Abschnitt 7.8.3 vorgenommenen Änderungen Anforderungen für den Fall enthält, dass Unsicherheiten hinsichtlich der Wirkung des Mediums auf die Bauteilintegrität bestehen.

Zu Abschnitt 5 "Konstruktive Gestaltung"

(1) Der Abschnitt 5 "Konstruktive Gestaltung" wurde an mehreren Stellen redaktionell überarbeitet, so dass die Vorgaben als Anforderungen an die konstruktive Gestaltung formuliert sind (z.B. Abschnitt 5.1.4.2, Abschnitt 5.3.2.4). Bei den Anforderungen an eine beanspruchungsgünstige Konstruktion wurden Temperaturschichtungen als Belastungsart aufgenommen.

(2) Im Abschnitt 5.2.4.1 wurde die Anforderung an die Schraubenanordnung in Flanschen im Einklang mit den Vorgaben des konventionellen Regelwerks präzisiert.

(3) Im Abschnitt 5.2.5 wurde durch Aufnahme des Absatzes 6 klargestellt, dass die konstruktive Gestaltung eine vorwiegende Zugbeanspruchung der Schrauben sicherzustellen muss.

(4) Die Abmessungsgrenzen für Stutzen in Abschnitt 5.2.6 wurden von "Innendurchmesser ≥ 120 mm" in " ≥ DN 125" geändert.

Zu Abschnitt 6 "Dimensionierung"

(1) Die Formulierungen in Abschnitt 6.1 wurden

aufgrund eines vom Bundesumweltministerium angemerkten formalen Widerspruchs zwischen den bisherigen Absätzen 2 und 5,
in Auswertung der RSK-Stellungnahme vom 24. Juli 2008 (410. Sitzung) "Festigkeitshypothesen im Anwendungsbereich des KTA-Regelwerks bei der Nachbewertung von Komponenten und Systemen; Bewertung sicherheitstechnischer Aspekte zur Frage der wahlweisen Verwendbarkeit der Festigkeitshypothesen nach von Mises und Tresca im KTA-Regelwerk",
in Auswertung der Stellungnahme des Unterausschusses Programm und Grundsatzfragen (UA-PG) zum Verständnis von KTA-Regeln, 33. Sitzung des UA-PG vom 10. März 2010
zur Aufnahme von Festlegungen zum Grenztragfähigkeitsnachweis

präzisiert und ergänzt. Hiermit soll erreicht werden, dass die Anforderungen an die Dimensionierung eindeutig vorgegeben werden und eine Fehlinterpretation der Anforderungen möglichst ausgeschlossen wird.

(2) Die Gleichung (6.5-3) wurde richtiggestellt.

(3) Die Festlegungen zu Plattierungen im Abschnitt 6.3 wurden präzisiert.

Zu den Abschnitten 7.1 bis 7.7

(1) Im Abschnitt 7.1.2 wurde klargestellt, dass Schweißnähte bei Ermüdungsanalysen zu berücksichtigen sind.

(2) Da die Zugrundelegung des tatsächlichen Spannungs-Dehnungs-Zusammenhangs bei elastischplastischen Analysen nicht immer zutrifft und hierfür auch keine konkreten Anforderungen festgelegt waren, wurde der letzte Satz in Abschnitt 7.3 (1) geändert.

(3) Im Rahmen der Nachweisführung wird bewertet, inwieweit bei der Modellabbildung die unterschiedlichen Einflussgrößen das Ergebnis beeinflussen können und in welchem Umfang sie in die Modellabbildung mit einzubeziehen sind. Zeigt diese Bewertung, dass eine unmittelbare Einbeziehung in das Modell nicht erforderlich ist, ist dem Erfordernis einer Berücksichtigung ausreichend Rechnung getragen. In den Absätzen 3 und 5 des Abschnitts 7.6.2.3 wurde deshalb die Formulierung einheitlich in "ist zu berücksichtigen" geändert.

(4) Im Rahmen der Regeländerungsverfahren KTA 3201.2 und KTA 3211.2 wurde die Möglichkeit geprüft, für die mechanische Systemanalyse (Abschnitt 7.6) Festlegungen zur Vorgehensweise bei der Analyse des Dämpfungsverhaltens für Betriebslastfälle in die Regel aufzunehmen. Es hat sich gezeigt, dass konkrete Festlegungen der Einzelfallbetrachtung vorbehalten bleiben müssen. Zur grundsätzlichen Vorgehensweise wird folgender Standpunkt vertreten:

Die wesentlichen Parameter einer dynamischen Rohrleitungsanalyse sind

die Berechnungsverfahren nach der "Modal-Analyse" bzw. der "direkten Integration",
die Wahl des Dämpfungsgrades für Betriebs- bzw. Störfälle,
die Berücksichtigung des sogenannten "Frequenz-Shiftes".

Bei dynamischen Rohrleitungsberechnungen wird zwischen der Modal-Analyse und der direkten Integration (Zeitverlaufsmethode) unterschieden. Beide Verfahren können gleichberechtigt verwendet werden. Als Dämpfungsparameter werden entweder eine konstante Dämpfung für alle Frequenzen oder eine frequenzabhängige Rayleigh-Dämpfung mit den zwei Parametern a und ß zugrunde gelegt. Aus Anwendersicht ist die einfachere Verwendung einer konstanten Dämpfung für alle Frequenzbereiche der Rayleigh-Dämpfung vorzuziehen, da hier die Dämpfungshyperbel zwischen 2 signifikanten Frequenzen "eingehängt" werden muss. Für die Festlegung dieser Einhängepunkte - z.B. erste Eigenfrequenz und eine ingenieurmäßig abgeschätzte höhere Eigenfrequenz in einer Größenordnung von ca. 60 Hz bis 80 Hz - sind ggf. aufwändige ingenieurmäßige Überlegungen bzw. Variationsrechnungen erforderlich.

Im amerikanischen ASME-Regelwerk wird für Rohrleitungen sowohl beim "Operational Basis Earthquake" (OBE) als auch beim "Safe Shutdown Earthquake"(SSE) ein Dämpfungsgrad von 5 % empfohlen (Section III, Division 1, - Appendices, table N-1230-1). Dieser Wert gilt unabhängig von der Frequenz. Um eine optimale betriebliche Auslegung der Rohrleitungen nicht durch zu strenge Forderungen an die Erdbebensicherheit zu behindern, ist der vorgeschlagene Dämpfungsgrad im Vergleich zu früheren Fassungen des ASME-Regelwerks erhöht worden. Berücksichtigt wurde dabei die Erfahrung, dass vergleichsweise flexibel trassierte Leitungen in fossil befeuerten Kraftwerken und in chemischen Anlagen beim Erdbeben nicht versagen.

Für die Wahl des Dämpfungswertes bei dynamischen Rohrleitungsanalysen wird im Wesentlichen auf KTA 2201.4 zurückgegriffen, aus der der üblicherweise angesetzte Dämpfungsgrad von 4 % für EVA-Lastfälle abgeleitet wird. Dieser Dämpfungsgrad von 4 % wird häufig auch für betriebliche Belastungen zugrunde gelegt.

Einen weiteren erheblichen Einfluss auf die Ergebnisse von dynamischen Rohrleitungsanalysen hat die Wahl des sogenannten Frequenz-Shiftes. Hierdurch sollen Ungenauigkeiten beim Ansatz der Systemmassen und geometrischen Längen dahingehend berücksichtigt werden, dass eventuelle Resonanzeffekte zwischen Eigen- und Anregungsfrequenz der Rohrleitung erkannt werden. In der Praxis wird häufig ein Frequenz-Shift von ± 2 % (beidseitig) als Indikator für eventuell auftretende Resonanzeffekte verwendet.

Ausführungen zur Schwingungsberechnung sind auch in der Richtlinie VDI 3842 "Schwingungen in Rohrleitungssystemen" (2004-06) enthalten.

(5) Zur Vermeidung von Fehlinterpretationen wurde die Definition der primären lokalen Membranspannung in Abschnitt 7.7.2.2 in Anlehnung an den ASME Code überarbeitet.

(6) Der Abschnitt 7.7.3 "Spannungsüberlagerung und Spannungsbeurteilung" wurde an einigen Stellen zwecks Klarstellung der Anforderungen präzisiert.

(7) Der in der Gleichung (7.7-7) mit aufgeführte Spannungsbegrenzungsterm R_p0,2T/1,5 (Dimensionierung nach Anhang a für austenitische Walz- und Schmiedestähle) war abweichend vom ASME Code (min{R_p0,2RT/1,5; R_p0,2T/1,1; R_mRT/3,0 ; R_mT/2,7}) mit aufgenommen worden, um den im Anhang a enthaltenen Dimensionierungsgleichungen, die nicht aus dem ASME Code, sondern aus deutschen technischen Regelwerken entnommen wurden, hinsichtlich der dort geforderten Spannungsbegrenzung zu entsprechen. Dies ist vor allem bei den Werkstoffen von Bedeutung, bei denen aufgrund der Werkstoffkennwerte die Dehngrenze R_pfür die Dimensionierung maßgebend wird und aufgrund des zugrunde liegenden Berechnungsverfahrens dann nicht mehr bei der Dimensionierung eine hinreichende Verformungsbegrenzung sichergestellt wäre. Ein Beispiel hierfür ist das Verformungsverhalten in gekrempten Böden.

Da das Spannungsabsicherungskonzept in der Analyse des mechanischen Verhaltens auf der Grundlage linearelastischer Spannungsanalysen unter Verwendung der Traglastfaktoren bei ungleichmäßiger Spannungsverteilung sich im Grundsatz nicht von demjenigen im konventionellen Regelwerk unterscheidet, wird es als angemessen angesehen, bei einer Dimensionierung mit Hilfe von Primärspannungsnachweisen hier die gleichen Spannungsgrenzen der Bemessung zugrunde zu legen.

Unter Berücksichtigung des vorstehend erläuterten, zusätzlichen Spannungsbegrenzungsterms sinkt das zulässige Spannungsniveau bei Primärspannungsnachweisen unter die vom ASME Code geforderte Spannungsbegrenzung für austenitische Werkstoffe auch für alle anderen Bauformen, für die eine Anpassung nicht erforderlich ist (z.B. für Zylinderschalen unter innerem Überdruck). Die vorgeschlagene Regelung für die Bildung des Spannungsvergleichswertes zum Zwecke der Dimensionierung stellt somit eine Vereinfachung dar, die additive Konservativitäten beinhaltet.

(8) In den Tabellen 7.7-4 bis 7.7-6 wurde für die Stufe 0 eine Fußnote in die Tabellen aufgenommen, die auf den neu geschaffenen normativen Anhang B verweist, der die Vorgehensweise bei einer erneuten Bewertung einer Komponente beschreibt.

In Tabelle 7.7-5 wurde die für austenitische Stähle in Stufe C geltende Primärspannungsbegrenzung so geändert, dass jeweils der größte Wert aus dem bisher festgelegten Sm-Wert und dem in Tabelle 7.7-6 für Stahlguss festgelegten Grenzwert anzuwenden ist. Dadurch wird sichergestellt, dass ein austenitischer Stahl genau so hoch beansprucht werden darf wie ein Stahlguss. Diese Regelung entspricht den Festlegungen im ASME Code.

Die Tabelle 7.7-7 wurde auf Basis der bisherigen Tabelle a 2.8-2 überarbeitet und um eine Spannungsbegrenzung zur Berücksichtigung des Torsionsmoments infolge des Montagevorgangs bei Verwendung eines Drehmomentenschlüssels erweitert. Die Tabelle wurde dabei so geändert, dass der Einbauzustand als separate Spalte erscheint und eine Angabe von zulässigen Spannungen für die Beanspruchungsstufe P nur im Prüfzustand erfolgt.

(9) Da nicht für jeden Lastfall eine Ermittlung der unteren Grenztraglast erforderlich ist, wurden im Abschnitt 7.7.4.2 in Absatz 6 Bedingungen festgelegt, unter denen die untere Grenztraglast für die einzelnen Beanspruchungsstufen proportional den unterschiedlichen Fließspannungen umgerechnet werden darf.

Zu Abschnitt 7.8 "Ermüdungsanalyse"

(1) An mehreren Stellen erfolgte eine Präzisierung der Formulierungen.

(2) Im Rahmen des Regeländerungsverfahrens erfolgte eine ausführliche Diskussion und Auswertung des nationalen und internationalen Kenntnisstandes zu den bei Ermüdungsanalysen für ferritische und austenitische Werkstoffe anzuwendenden Ermüdungskurven. Hierbei wurde der Einfluss des Mediums ausführlich behandelt.

(3) Bei KTA 3201.2 in der Fassung 1996-06 lag die aus den 1960er Jahren stammende ASME Auslegungskurve ("Langer-Curve" [1]) unter Berücksichtigung unterschiedlicher Elastizitätsmoduln zu Grunde. Die Auswertung umfangreicher neuerer Versuchsergebnisse aus den USa und Japan für austenitische Werkstoffe zeigen, dass die der ursprünglichen (alten) ASME Auslegungskurve zu Grunde liegende Mittelwertkurve (an Luft) im Bereich ab 104 Lastwechsel nichtkonservative Ergebnisse liefern kann [2] (NUREG/CR-6909).

Aus diesem Grund wurde mit der Veröffentlichung der Ausgabe ASME 2009b, Section III, im Appendix I eine neue Auslegungskurve für austenitische Werkstoffe eingeführt. Die neue Auslegungskurve zeigt im Vergleich zur alten Auslegungskurve folgende Änderungen:

Im Kurzzeitfestigkeitsbereich 10¹bis 5
⋅ 10²Lastwechsel höhere zulässige Spannungsamplituden oder bei vorgegebener Spannungsamplitude eine höhere zulässige Lastwechselzahl.
Im Bereich von 10³bis 10⁷Lastwechsel geringere zulässige Spannunsamplituden oder bei vorgegebener Spannungsamplitude eine geringere zulässige Lastwechselzahl.
Aufnahme des hochzyklischen Bereiches bis 10¹¹Lastwechsel.
Entfall der Kurven A-C.

In wieweit die neue ASME Auslegungskurve in Luftumgebung auf die in den deutschen Kernkraftwerken eingesetzten stabilisierten austenitischen Werkstoffe 1.4550 und 1.4541 übertragbar und anwendbar ist, wurde im Rahmen von Forschungsvorhaben untersucht ([3] bis [7]). Anhand dieser Versuchsergebnisse wurden für Luftumgebung eigenständige Mittelwertskurven für Raumtemperatur und Temperaturen > 80 IC abgeleitet und darauf basierend neue Auslegungskurven [8] bis [10]. Im Gegensatz zu den Auswertungen in NUREG/CR-6909 [2], wo von keinem Einfluss der Temperatur auf die Mittelwertkurve an Luft ausgegangen wird, zeigten die Untersuchungen in [3], [5] und [7] einen nicht vernachlässigbaren Temperatureinfluss im Bereich ab 10⁴Lastwechsel. Aus diesem Grund erfolgt explizit für die stabilisierten austenitischen Stähle 1.4541 und 1.4550 die Herleitung von Mittelwert- und Auslegungskurven für Raumtemperatur und Temperaturen > 80 IC [8]. In den USa wird der Temperatureinfluss auf die Mittelwertkurve in Luftumgebung als nicht signifikant bewertet (NUREG/CR-6909 [2] Kap. 5.1.3). Deshalb wird im ASME Code keine Differenzierung der Auslegungskurve bezüglich der Temperatur vorgenommen. Bei der Bewertung des Mediumeinflusses mit Fen-Faktoren wird die Temperatur explizit berücksichtigt [2]. Für die übrigen austenitischen Stähle wurden die Auslegungskurven des ASME Code ab Ausgabe ASME 2009b übernommen. Für die ferritischen Werkstoffe bleiben die bisherigen Auslegungskurven bestehen.

(4) Hinsichtlich einer quantitativen Bewertung des Einflusses des Mediums auf die Ermüdungsfestigkeit wurden in den Forschungsvorhaben [11] bis [14] Versuche durchgeführt und vergleichend zu dem in NUREG/CR-6909 [2] gezeigten "Environmental Factor" F_enbewertet. Damit liegen anhand der durchgeführten Laboruntersuchungen zwar Bewertungskriterien zur Erfassung des Mediumeinflusses auf das Ermüdungsverhalten vor, dieses wird allerdings als konservativ bewertet. International liegt derzeit noch keine einheitliche Vorgehensweise zur Erfassung eines möglichen Mediumeinflusses auf die Ermüdung in den Regelwerken vor. Dies wird insbesondere bei der Berechnung von F_enin den Berichten [15] und [16] deutlich.

International existieren in der Fachwelt verschiedene Berechnungsverfahren zur Berücksichtigung des Mediumeinflusses. Neben dem Verfahren nach NUREG/CR 6909 existieren weitere numerische Ansätze. Hierzu zählt der Approximationsansatz des Argonne National Laboratory (ANL), veröffentlicht im Bericht ANL-LWRS47 sowie ein auf dem ASME Code Meeting, "Section III Subgroup on Fatigue Strength", Nashville TN, May 15, 2012, diskutiertes Verfahren. Ein Vorschlag für eine ausführliche Anleitung zur rechnerischen Vorgehensweise findet sich in [16]. Eine weitere Vereinheitlichung der US amerikanischen Vorgensweise kann erwartet werden [17], wenn Ende 2014 die Revisionen von NUREG/CR-6909 [2] und von Reg. Guide 1.207 [18] veröffentlicht werden.

Die bisherigen Laboruntersuchungen unter Mediumsbedingungen erfolgten fast ausschließlich mit konstanten einachsigen Beanspruchungsbedingungen. Neuere Erkenntnisse deuten auf einen lebensdauerbegünstigenden Einfluss betriebsnaher langer Haltezeiten hinsichtlich der Belastungen hin (Haltezeiteffekt). Dieses gilt hierbei sowohl für Luftumgebung, als auch für LWR-Mediumsbedingungen, z.B. [19] bis [22]. Eine Berücksichtigung dieses Effektes ist nach Vorliegen abgesicherter experimenteller Untersuchungen, falls erforderlich, vorgesehen.

Für eine statistisch abgesicherte Quantifizierung der Verteilung der anteiligen Beiträge von Temperatureinfluss und Mediumeinfluss liegen derzeit nicht genügend Untersuchungsergebnisse vor. Erste Untersuchungen zeigen jedoch den Einfluss der Temperatur unter verschiedenen Umgebungsbedingungen (Vakuum, Luft und Medium) [23]. Es zeigt sich, dass der aktuell in experimentellen Untersuchungen nachgewiesene lebensdauerbegrenzende Einfluss des Mediums bereits einen derzeit nicht quantifizierbaren Anteil des Temperatureinflusses enthält, der abhängig von der Dehnungsamplitude bzw. der zulässigen Zyklenzahl ist [24].

Vorliegende Untersuchungsergebnisse zum Mediumeinfluss mit realistischen transienten Dehnungsverläufen von AREVA-SAS zeigen, dass die ursprüngliche (alte) ASME Auslegungskurve für Austenit sowohl in Luft als auch unter moderaten Mediumsbedingungen (zugrunde gelegter Fen-Faktor: F_en= 3) weiterhin konservative Ergebnisse liefert ([25] - [27]).

Beruht die Ermittlung der Ermüdungsfestigkeit auf den tatsächlich aufgetretenen ermüdungsrelevanten Lastereignissen, kann im Sinne der Schadensvorsorge der aus Laborversuchen bestätigte reduzierende Einfluss des Mediums, insbesondere, wenn der Einfluss des Mediums nicht mehr als moderat angesehen werden kann, nicht grundsätzlich vernachlässigt werden.

In Abschnitt 7.8.3 (2) sind entsprechende Maßnahmen zur Berücksichtung des Mediumeinflusses aufgeführt. Auswertungen unter Berücksichtigung der nach den existierenden Verfahren anzusetzenden Einflussfaktoren für die in deutschen Anlagen (DWR und SWR) vorhandenen Bedingungen (Werkstoff, Temperatur, Sauerstoffkonzentration, Dehnrate) ergaben, dass die Anwendung von Aufmerksamkeitsschwellen sachgerecht ist. Als Aufmerksamkeitsschwelle wurde sowohl für ferritische als auch für austenitische Werkstoffe der Wert D = 0,4 festgelegt. Erfolgt die Festlegung der nach Abschnitt 7.8.3 (2) erforderlichen Maßnahmen anhand von Ermüdungsbewertungen, die auf Basis der Ermüdungskurve 7.8-2 in KTA 3201.2 (1996-06) erstellt wurden, wird bei austenitischen Werkstoffen anstelle des Wertes D = 0,4 der Wert D = 0,2 als sachgerecht angesehen.

Die Berechnung zur Berücksichtigung des Mediumeinflusses wird auf Basis der Auslegungskurven an Luft durchgeführt (siehe z.B. [2], [16]).

Alternativ kann der Einfluss des Mediums auf die Ermüdung durch detaillierte Nachweise unter Berücksichtigung der Temperatur, des Sauerstoffgehalts und der Dehnungsänderungsgeschwindigkeit, z.B. unter Anwendung der oben genannten Verfahren oder durch experimentelle Nachweise erfasst werden. Prinzipiell ist zur Berücksichtigung des Mediumeinflusses die oben genannte Vorgehensweise anwendbar. Untersuchungen deuten jedoch darauf hin, dass die hieraus abzuleitenden Fen-Faktoren in vielen Fällen konservativen Charakter tragen. Laboruntersuchungen zeigen, dass bei Berücksichtigung der Interaktion zwischen Oberflächen- und Mediumeffekt sowie bei Verwendung betriebsnaher Belastungssignale auf experimentellem Wege erhebliche Reserven nachgewiesen werden können, [24] bis [28]. Durch gezielte experimentelle Untersuchungen ist somit eine Quantifizierung von Konservativitäten möglich. Dies ermöglicht eine teilweise Abdeckung dieses Einflusses des Mediums durch die bestehenden Auslegungskurven und die Ableitung zulässiger Fen-Faktoren "Fen,allowable" (siehe hierzu das in [28] beschriebene Verfahren, dessen Umsetzung im französischen RCC-M-Code diskutiert wird). Darauf deuten auch Untersuchungen der MPA-Stuttgart hin [9]. Aufgrund der konservativen Auslegung, der betrieblichen Maßnahmen und der vorbeugenden Instandhaltung zeigt die Betriebserfahrung der deutschen LWR-Anlagen, dass das vorhandene Medium keinen signifikanten Einfluss auf die Lebensdauer der Komponenten hat.

Die Definition von Aufmerksamkeitsschwellen wird im Sinne eines konservativen Vorgehens im Rahmen der Regelwerkserstellung dem Umstand gerecht, dass sich auf Basis von Laborversuchen Hinweise bezüglich eines Einflusses des Mediums auf die Ermüdungsfestigkeit ergeben. Sollte sich der Kenntnisstand zu diesem Einfluss in Zukunft weiterentwickeln, so ist dann auf dieser neuen Basis über die Festlegung in KTA 3201.2 zur Höhe der Aufmerksamkeitsschwellen bzw. gegebenenfalls auch über deren Entfall zu entscheiden. Die Festlegung der Aufmerksamkeitsschwellen stellt ein den aktuellen Kenntnisstand zum Thema Mediumeinfluss widerspiegelndes pragmatisches und in der Betriebspraxis umsetzbares Verfahren dar, das in der internationalen Regelwerkslandschaft bisher Alleinstellungscharakter hat.

[1]	Langer, B. F.: Design of Pressure Vessels for Low-Cycle Fatigue, Journal of Basic Engineering, 84(3), 1962, pp. 389-402.
[2]	Chopra O. K. and Shack, W. J.: Effect of LWR Coolant Environments on the Fatigue Life of Reactor Materials, NUREG/CR-6909, ANL-06/08, 2007
[3]	Herter, K.-H., Reicherter B., Schuler X.: Nachweis der Ermüdungsfestigkeit bei kerntechnischen Komponenten aus ferritischen und austenitischen Werkstoffen, BMWi Reaktorsicherheitsforschung - Kennzeichen 1501296, MPa Universität Stuttgart, Juni 2009
[4]	Hoffmann, M., Herter K.-H., Schuler X.: Experimentelle Untersuchungen zur Ermittlung der Ermüdungsfestigkeit der austenitischen Plattierung von kerntechnischen Komponenten, BMU Vorhaben 3611 R01.306, MPa Universität Stuttgart, Nr. 8428.000 000, Abschlussbericht, April 2012
[5]	Herter, K.-H., Fesich T., Schuler X.: "Sicherheitsbewertung kerntechnischer Komponenten bei komplexer mehrachsiger Schwingbeanspruchung, BMWi-Vorhaben 1501392, MPa Universität Stuttgart, Abschlussbericht, Dezember 2012
[6]	Herter, K.-H., Schuler X., Weissenberg T.: Fatigue behavior of nuclear material under air and environmental conditions, 2013 ASME Pressure Vessel and Piping Conference, PVP2013-97394, Paris
[7]	Rudolph, J.; Willuweit, A.; Bauerbach, K.; Beier, H. Th.; Schlitzer, T.; Vormwald, M.; Fischaleck, M.; Scholz, A.: Numerische Simulation und experimentelle Charakterisierung des Ermüdungsrisswachstums unter thermozyklischer Beanspruchung. BMBF Verbundforschungsvorhaben "Grundlagen des System-, Ausström- und Werkstoffverhaltens von Rohrleitungen bei thermischer Wechselbeanspruchung", Verbundvorhaben "Thermische Wechselbeanspruchung", Verbundprojekt 02NUK009D
[8]	Schuler, X.: MPa Aktennotiz Shr vom 02.10.2012: Ermüdungskurven für austenitische Werkstoffe in Luftumgebung im Anwendungsbereich der KTA 3201.2 und KTA 3211.2
[9]	Herter K.-H., Schuler X., Wei ßenberg T.: Fatigue behaviour and crack growth of ferritic steel under environmental conditions. 38. MPA-Seminar, 1.-2. Oktober 2012, Stuttgart
[10]	Schuler X., Herter K.-H., Rudolph J.: Derivation of design fatigue curves for austenitic stainless steel grades 1.4541 and 1.4550 within the German nuclear safety standard KTA 3201.2, 2013 ASME Pressure Vessel and Piping Conference, PVP2013-97138, Paris
[11]	Waidele H., Weißenberg T. : Zentrale Untersuchung und Auswertung von Herstellungsfehlern und Betriebsschäden im Hinblick auf druckführende Anlagenteile von Kernkraftwerken, Arbeitspaket 3, Einfluss des Reaktorkühlmediums auf das Ermüdungsverhalten austenitischer Rohrleitungen, BMU-Vorhaben SR 2501, MPa Universität Stuttgart, November 2007
[12]	Weißenberg T.: Ermüdungsverhalten ferritischer Druckbehälter- und Rohrleitungsstähle in sauerstoffhaltigem Hochtemperaturwasser, Abschlussbericht, BMWi Reaktorsicherheitsforschung - Kennzeichen 1501309, MPa Universität Stuttgart, September 2009
[13]	Weißenberg T.: Rissverhalten ferritischer Druckbehälterstähle in sauerstoffhaltigem Hochtemperaturwasser bei transienten Vorgängen, Risskorrosion Phase 1: Rissinitiierung und Risswachstum, Teilbericht A: Experimentelle Risskorrosionsuntersuchungen, Abschlussbericht, Forschungsvorhaben 1501319, MPa Universität Stuttgart, August 2010
[14]	Weißenberg T.: Zentrale Untersuchung und Auswertung von Herstellungsfehlern und Betriebsschäden im Hinblick auf druckführende Anlagenteile von Kernkraftwerken, Arbeitspaket 3.1, Untersuchung des Einflusses von Reaktorkühlmedium auf das Ermüdungsverhalten austenitischer CrNi-Stähle, BMU-Vorhaben SR0801312, MPa Universität Stuttgart, Juni 2011
[15]	EPRI Technical Report No. 1023012, Environmentally Assisted Fatigue Gap Analysis and Roadmap for Future Research, Gap Analysis Report, Final Report, December 2011, EPRI, Palo Alto, CA: 2011.1023012
[16]	EPRI Technical Report No. 1025823, Guidelines for Addressing Environmental Effects in Fatigue Usage Calculations, Final Report, December 2012, EPRI, Palo Alto, CA: 2012.1025823
[17]	Stevens G.L.: summary of NUREG/CR-6909, Rev. 1 and Suggestions for Future EAF Work, February 12, 2013, ASME Section III Subgroup on Fatigue Strength, Los Angeles, CA
[18]	Regulatory Guide 1.207: Guidelines for evaluating fatigue analyses incorporating the life reduction of meatal components due to the effects of the lightwater reactor environment for new reactors, U.S. NRC, March 2007
[19]	Hälbig J., Ilg U., König G., Reese S.: Ermüdungskurven für austenitische Strukturwerkstoffe im Geltungsbereich des KTA-Regelwerkes unter Berücksichtigung des aktuellen Kenntnisstandes. Design Fatigue Curves for austenitic stainless steel structures in accordance with the German KTA Safety Standards considering the current knowledge. 37. MPA-Seminar, 6.-7. Oktober 2011, Stuttgart)
[20]	Solin J., Reese S.H., Mayinger W.: Fatigue Performance of Stainless Steel in NPP Service Conditions. PVP2012- 78721. Proceedings of the ASME 2012 Pressure Vessels & Piping Division Conference PVP2012, July 15-19, 2012, Toronto, Ontario, Canada
[21]	Roth A., Devrient B.: Environmental Effects on Fatigue - Possible Reasons for the Apparent Mismatch Between Laboratory Test Results and Operational Experience. fontevraud 7. 26.-30. September 2010, Paper Reference No A031 -T05
[22]	Roth A.: News From Hold-Time-Effects in Fatigue. Workshop, Ermüdungsverhalten von Bauteilen unter Berücksichtigung des Mediumeinflusses, 8. Juni 2011. MPa Stuttgart
[23]	De Baglion L., Mendez J., Le Duff J.-A., Lefrançois A.: Influence of PWR Primary Water on LCF Behavior of type 304L Austenitic Stainless Steel at 300 IC - Comparison with Results obtained in Vacuum or in Air. PVP2012-78767. Proceedings of the ASME 2012 Pressure Vessels & Piping Conference PVP2012, July 15-19, 2012, Toronto, Ontario, Canada
[24]	Reese S.H., Solin J., Klucke D., Karabaki H. E.: Fatigue performance of stabilized austentic stainless steels in terms of environmental fatigue factors, temperature and hold time effects. Jahrestagung Kerntechnik 2013, 14.-16. Juni 2013, Berlin
[25]	Le Duff J.-A., Lefrançois A., Vernot J.P.: Effects of Surface Finish and Loading Conditions on the Low Cycle Fatigue Behavior of Austenitic Stainless Steel in PWR Environment. Comparison of LCF Test Results with NUREG/CR-6909 Life Estimations. PVP2008-61894. Proceedings of PVP2008 2008 ASME Pressure Vessels and Piping Division Conference, July 27-31, 2008, Chicago, Illinois, USA
[26]	Le Duff J.-A., Lefrançois A., Vernot J.P.: Effects of Surface Finish and Loading Conditions on the Low Cycle Fatigue Fatigue Behavior of Austenitic Stainless Steel in PWR Environment for various Strain Amplitude Levels. PVP2009-78129. Proceedings of the ASME 2009 Pressure Vessels and Piping Division Conference PVP2009, July 26-30, 2009, Prague, Czech Republic
[27]	Le Duff, J.-A.; Lefrançois, A.; Vernot, J.P.; Bossu, D.: Effect of loading signal shape and of surface finish on the low cycle fatigue behavior of 304L stainless steel in PWR environment. PVP2010-26027. Proceedings of the ASME 2010 Pressure Vessels & Piping Division / K-PVP Conference PVP201 0, July 18-22, 2010, Bellevue, Washington, USA
[28]	Courtin, S.; Lefrançois, A.; Le Duff, J.-A.; Le Pécheur, A.: Environmentally Assisted Fatigue Assessment considering an alternative Method to the ASME Code Case N-792. PVP2012-78088. Proceedings of the ASME 2012 Pressure Vessels & Piping Conference PVP2012, July 15-19, 2012, Toronto, Ontario, Canada

Zu Abschnitt 7.9 "Sprödbruchanalyse"

(1) Es wurde eine Trennung der Anforderungen an die Sprödbruchanalyse im Rahmen der Auslegung und von in Betrieb befindlichen RDB vorgenommen. Die Anforderungen an die Sprödbruchanalyse im Rahmen der Auslegung werden auch zukünftig in KTA 3201.2 geregelt, während spezielle Anforderungen an die Sprödbruchanalyse von in Betrieb befindlichen RDB zukünftig in KTA 3201.4 festgelegt sind. Diese Trennung wurde deshalb vorgenommen, weil für in Betrieb befindliche RDB Ergebnisse aus wiederkehrenden Prüfungen vorliegen und auf dieser Grundlage andere Fehlerannahmen möglich sind als bei der Auslegung (Ergebnisse der zerstörungsfreien Prüfung anstelle eines postulierten T/4-Fehlers). Während des Betriebes kann es außerdem erforderlich sein, die Gültigkeit des im Rahmen der Auslegung geführten Sprödbruchsicherheitsnachweises zu überprüfen, z.B. wenn sich die Randbedingungen geändert haben. Hierfür waren in KTA 3201.4 bisher keine Anforderungen enthalten.

(2) Der Lastpfadverlauf des Rissantriebs kann z.B. bei der Bewertung großer Fehlerpostulate die Bruchzähigkeitshochlage erreichen und im weiteren Verlauf wieder unterschreiten, wobei sich im Hochlagenbereich eine Vergrößerung des Fehlerpostulats durch duktiles Risswachstum ergeben kann. Deshalb ist zu prüfen, ob für die Sprödbruchanalysen ein zu berücksichtigender Einfluss auf die Fehlergröße resultiert (Abschnitt 7.9.1 (6)). Das Ziel der Anforderungen in 7.9.1 (6) besteht darin, den Anwendungsbereich der Materialkurve zu begrenzen.

(3) Bei der Berechnung des Rissantriebs K_Ifür betriebliche Lastfälle werden der Membranspannungsanteil K_Imaus dem Betriebsdruck und der Anteil K_Ithaus dem Temperaturprofil der Reaktordruckbehälterwand addiert, K_I= K_Im+ K_Ith. Zur Abdeckung eines Rissantriebanteils K_Ieigenaus evtl. nach Spannungsarmglühung und Betrieb verbliebenen Eigenspannungen, wird K_Ium einen Sicherheitszuschlag in der Größe von K_Imerhöht, K_I= 2K_Im+ K_Ith[1]. Der niedrigste Rissantrieb K_Imergibt sich mit dem Abschaltdruck der Hauptkühlmittelpumpen, der von der erforderlichen Druckdifferenz für die Funktion der Wellendichtungen abhängt [2]. Bei zu niedrigem Betriebsdruck, wie mit der niedrigen erforderlichen Druckdifferenz moderner Wellendichtungen möglich, könnte K_Im < K_Ieigenwerden, sodass der Eigenspannungsanteil K_Ieigennicht mehr mit dem Faktor 2 auf K_Imabgedeckt wäre. Deshalb wurden beide Möglichkeiten zur Berechnung des Rissantriebs in den Regeländerungsvorschlag aufgenommen, K_I= 2K_Im+ K_Ithund K_I= K_Im+ K_Ieigen+ K_Ith, wobei das höhere Ergebnis für die Sprödbruchanalyse zugrunde zu legen ist (Gleichung 7.9-4).

[1]	PVRC Recommendations on Toughness Requirements for Ferritic Materials, Welding Research Council (WRC) Bulletin 175, August 1972
[2]	Technical Basis for Revised p-Tlimit Curve Methodology, Bamford, W.H., Stevens, G.L., Griesbach, J.G., Malik, S.N., PVP-Vol. 407, Pressure Vessel and Piping Codes and Standards-2000, ASME 2000

(4) Für den Ausschluss der Sprödbruchinitiierung bei den Stufen a und B wurde seit etwa 1970 die als Lower Bound der Rissarrestzähigkeitsdatenbasis des ASME Code definierte Referenzbruchzähigkeitskurve KIR als Lower Bound der Bruchzähigkeit K_Icverwendet.

Zur Anpassung an einen weiter fortgeschrittenen Kenntnisstand wurde die K_IR- durch die K_Ic-Kurve ersetzt (Gleichung 7.9-4).

Diese Änderung folgt einem seit 1970 weiter fortgeschrittenen Kenntnisstand, der in gleicher Weise im ASME Code berücksichtigt wurde. Mit dem bisherigen Vorgehen sollten bei den Bruchzähigkeitsmessungen beobachtete pop in-Ereignisse abgedeckt werden, die als Möglichkeit für Sprödbruchinitiierung am Bauteil eingeschätzt wurden, was nach aktuellem Kenntnisstand nicht der Fall ist.

Im Bruchmechanikdiagramm wird mit dieser Änderung der inhärent immer vorhanden gewesene Sicherheitsabstand aus dem Abstand zwischen K_IR- und K_Ic-Kurve offen dargestellt

[1]	Inherent margin in the brittle failure assessment for RPV, D. Siegele, I. Varfolomeyev, G. Nagel, Pressure Vessels and Piping, 2008

(5) Die Höhe der Bruchzähigkeit nach Warmvorbelastung K_FRACwird durch den Lastpfad des Rissantriebs bestimmt und kann berechnet werden. Hierzu wurden jüngere deutsche Ergebnisse mit Validierung für deutsche Werkstoffe in die Regel aufgenommen [1-5]. Unabhängig davon dürfen auch Beziehungen im internationalen Regelwerk, wie z. B im British Standard 7910, verwendet werden (7.9.3.1 (1), 7.9.3.3 (3), Abschnitt D2 "Ermittlung der Bruchzähigkeit nach Warmvorbelastung" neu aufgenommen).

[1]	Werkstoffmechanisches Verhalten von postulierten Anrissen in druckführenden Komponenten mit vorbeanspruchter Rissspitze bei Belastungen infolge rascher Abkühlvorgänge, Schwerpunkt: Einfluss unterschiedlicher Werkstoffeigenschaften und Probengrößen, MPA-Abschlussbericht 86 67 00.000 (1997)
[2]	Werkstoffmechanisches Verhalten von postulierten Anrissen in druckführenden Komponenten mit vorbeanspruchter Rissspitze bei Belastungen infolge rascher Abkühlvorgänge, Schwerpunkt: Einfluss der Risslänge und der Dehngeschwindigkeit, IWM-Abschlussbericht T3/98, Freiburg (1998)
[3]	Werkstoffmechanisches Verhalten von postulierten Anrissen in druckführenden Komponenten mit vorbeanspruchter Rissspitze bei Belastungen infolge rascher Abkühlvorgänge, BAM-Abschlussbericht 234, Berlin (2000)
[4]	Werkstoffmechanisches Verhalten von postulierten Anrissen in druckführenden Komponenten mit vorbeanspruchter Rissspitze bei Belastungen infolge rascher Abkühlvorgänge, Schwerpunkt: Einfluss und Bedeutung der Mikrostruktur und der Mikrogeometrie, Abschlussbericht 03/98, Ottovon-Guericke-Universität, Magdeburg (1998)
[5]	MPA/VGB-Forschungsvorhaben 5.1, Untersuchungen zum Warm Prestress Effect, Abschlussbericht 944.705 100 (12/1998)

(6) Die bisher mögliche Nachweisführung in den Beanspruchungsstufen C und D unter Verwendung des Rissarrestes wurde gestrichen. Dadurch wurde auch für die Stufen C und D ein definierter Sicherheitsabstand geschaffen. Durch die Vorgabe für die Beanspruchungsstufen C und D, dass ein doppelt so großer Fehler als der sicher auffindbare Fehler den Sprödbruchanalysen zugrunde zu legen ist, wird ein Sicherheitsabstand von 2 auf die Fehlergröße und von ca. 1,4 bezogen auf den Spannungsintensitätsfaktor (Rissbeanspruchung) festgelegt. Auch hier erfolgt die Auswertung über die gesamte Rissfront.

(7) Für die Justierung der Bruchzähigkeitskurve K_Ic auf der Temperaturachse nach dem Referenztemperaturkonzept steht funktional gleich zur Referenztemperatur RT_NDT die Referenztemperatur RT_Todes Masterkurvenkonzepts zur Verfügung. Für die Anwendung der RT_Tokönnen die ASME Code Cases N-629 [1] und N-631 [2] sowie die Guideline TRS 429 der IAEa [3] herangezogen werden. Die RT_Toist direkt bruchzähigkeitsbasiert ermittelt und kann deshalb als Vergleichsnormal zur Überprüfung der Konservativität der mit der Sprödbruchübergangstemperatur T_NDTdes Fallgewichtsversuchs und der Indextemperatur T68 der Kerbschlag-Temperaturkurve ermittelten RT_NDTverwendet werden, wie z.B. in [4] und auch bei mehreren Sprödbruchsicherheitsnachweisen durchgeführt. Die Festlegung der bei Verwendung von RT_To erforderlichen Sicherheitszuschläge erfolgte auf Basis der IAEa Guideline TRS 429 [3] nach dem Vorbild der Adjusted Reference Temperature (ART) des Regulatory Guide 1.99 der U.S. NRC. Es wird für erforderlich gehalten, dass die Anwendung der..Adjusted Reference Temperature (ART) bei der nächsten Uberarbeitung in KTA 3203 geregelt wird. Die Validierung der RT_To mit deutschen Reaktordruckbehälterwerkstoffen [4-9] ergab, dass die Konservativität der RT_To ohne zusätzliche Sicherheitszuschläge gegeben ist [4] [5]. In Nacherprobungsprogrammen wurden die RT_To für die Werkstoffe im kernnahen Bereich und den Flansch für mehrere deutsche Reaktordruckbehälter ermittelt, sodass die RT_To bei der Aktualisierung der Sprödbruchsicherheitsnachweise bereits parallel zur RT_NDT mit angewendet wurde [10]. Im Unterschied zur RT_NDT ermöglicht die RT_To die werkstoffrepräsentative Darstellung der Bruchzähigkeit. Sie entspricht im Vergleich zur RT_NDT einem weiter fortgeschrittenen Nachweisstand, ist für deutsche Reaktordruckbehälterwerkstoffe validiert, wurde bereits in den Sprödbruchsicherheitsnachweisen mehrerer Reaktordruckbehälter parallel zur RT_NDT mit angewendet und ist seit 2001 auch in KTA 3203 (2001-06) enthalten. Die RT_To wurde deshalb als im Referenztemperaturkonzept funktional gleichwertige Alternative zur RTNDT in die Regel aufgenommen (7.9.4.1).

[1]	ASME Code Case N-629, Use of Fracture Toughness Data to Establish Reference Temperature for Pressure Retaining Materials, Section XI, Division 1, 2002
[2]	ASME Code Case N-631, Use of Fracture Toughness Data to Establish Reference Temperature for Pressure Retaining Materials Other Than Bolting for Class 1 Vessels, Section III, Division 2, 2002
[3]	IAEa TRS 429, Guidelines for Application of the Master Curve Approach to Reactor Pressure vessel Integrity in Nuclear Power Plants, Wien, 2005,
[4]	Der deutsche RDB-Sicherheitsnachweis - Untermauerung der Vorgehensweise durch ergänzende Kennwertermittlung in den Heißen Zellen, Elisabeth Keim, Hieronymus Hein, Arnulf Gundermann, Harald Hoffmann, Günter König, Ulf Ilg, Gerhard Nagel, Martin Widera, Daniel Rebsamen, 34. MPA-Seminar, 9./10. Oktober 2008, Stuttgart
[5]	Validation of RTTo for German Reactor Pressure Vessel Steels, Dieter Siegele, Elisabeth Keim, Gerhard Nagel, Journal of Pressure Vessel Technology, August 2008, Vol. 130
[6]	Ermittlung von Bruchmechanikkennwerten mittels vorbestrahlter Proben an Werkstoffen der deutschen DWR-Baulinien. Einordnung der Ergebnisse in das Master-Kurve-Konzept, RS-Vorhaben 1501284 des BMWi, ARE-VA, Erlangen, 30.9.2008
[7]	Kritische Überprüfung des Masterkurven-Ansatzes im Hinblick auf die Anwendung bei deutschen Kernkraftwerken, RS-Vorhaben 1501.240 des BMWi, MPA, Stuttgart, Februar 2006
[8]	Kritische Überprüfung des Masterkurven-Ansatzes im Hinblick auf die Anwendung bei deutschen Kernkraftwerken, RS-Vorhaben 1501.239 des BMWi, IWM, Freiburg, 9.3.2005
[9]	Anwendung des Master Curve-Konzepts zur Charakterisierung der Zähigkeit neutronenbestrahlter Reaktordruckbehälterstähle, RS-Vorhaben des BMWi, FZD, Dresden, Juli 2007
[10]	Inherent margin in the Brittle Failure Assessment for RPV, Dieter Siegele, Igor Varfolomeyev, Gerhard Nagel, Pressure Vessels and Piping Conference, 2008, Chicago USA, PVP 2008-61507

(8) Es ist üblich, die Bruchzähigkeit an tief angerissenen Proben mit einer hohen Mehrachsigkeit des Spannungszustands zu ermitteln, die etwa dem ebenen Dehnungszustand entspricht. Im Unterschied dazu kann am Bauteil eine niedrigere Mehrachsigkeit vorliegen, sodass die an der Probe gemessene Bruchzähigkeit nicht bauteilrepräsentativ übertragbar ist. Dieser Unterschied kann über die Querdehnungsbehinderung, englisch auch Constraint, quantifiziert und im Sprödbruchsicherheitsnachweis berücksichtigt werden (7.9.4.2) [1] - [5].

[1]	Kritische Überprüfung des Masterkurven-Ansatzes im Hinblick auf die Anwendung bei deutschen Kernkraftwerken, RS-Vorhaben 1501.239 des BMWi, IWM, Freiburg, 9.3.2005
[2]	Validation of constraint based methodology in structural integrity (VOCALIST-Programm), EURATOM, Final report July 2006
[3]	Inherent margin in the brittle failure assessment for RPV, D. Siegele, I. Varfolomeyev, G. Nagel, Pressure Vessels and Piping, 2008
[4]	Ergebnisse von Kleinproben und Anwendung von Modellansätzen zur bruchmechanischen Bewertung der RDB-Integrität, E. Keim, M. Hümmer, H. Hoffmann, G. Nagel, K. Küster, U. Ilg, G. König, M. Widera, D. Rebsamen, 34. MPA-Seminar, 9./10. Oktober 2008, Stuttgart
[5]	Transferability of irradiated materials to structures (TIMES-Programm), Application of local approach model within a case study, M. Hümmer, E. Keim, H. Hoffmann, Pressure Vessels and Piping, 2008

(9) Die Bilder zu Abschnitt 7.9 wurden überarbeitet und ergänzt, wobei u.a.

in Bild 7.9-1 eine Anpassung an die in den aktuellen ASME Code eingeflossene Datenbasis erfolgte (Weiterführung der K_Ic-Kurven bis 240 Mpa√ m),
Störfälle ohne Rissinitiierung und eine durchtrennt postulierte Plattierung berücksichtigt wurden.

Zu Abschnitt 7.12 "Spannungs-, Verformungs- und Ermüdungsanalysen für Flanschverbindungen"

(1) Die Anforderungen wurden an die aktualisierten Abschnitte a 2.8 bis a 2.10 angepasst, die auch die Spannungsanalyse für Flansche und Schrauben abdecken und immer gesicherte Angaben des Dichtungsherstellers fordern.

(2) In Abschnitt 7.12.1 (5) wurde klargestellt, dass die Spannungen nach Tabelle 7.7-7 zu begrenzen sind.

Zu Abschnitt 7.13 "Vermeidung des Versagens infolge thermisch bedingter fortschreitender Deformation"

(1) Die Gleichungen zur Ermittlung des plastischen Dehnungsinkrements AF- beim vereinfachten Nachweis wurden durch Fallunterscheidungen so umgestellt, dass keine negativen Einzelanteile mehr auftreten können. Sie sind somit für den Anwender eindeutig formuliert.

(2) Als mögliche Alternative für den Ratchetingnachweis kommt die Anwendung der Vereinfachten Fließzonentheorie in Betracht (siehe hierzu z.B. H. HÜBEL: Vereinfachte Fließzonentheorie, Bauingenieur Bd. 73, 1998, Nr. 11, S. 492-502).

Zu Abschnitt 8.1 "Komponentenspezifische Analyse des mechanischen Verhaltens; Allgemeines"

(1) In Absatz 1 wurde klargestellt, dass alle in Abschnitt 8 angegebenen komponentenspezifischen Analysen und Festigkeitsnachweise anerkannte und gebräuchliche Berechnungsverfahren darstellen und, wenn mehrere Verfahren angegeben sind, alle angegebenen Verfahren innerhalb ihrer Anwendungsgrenzen gleichwertig zugelassen sind.

(2) Im Absatz 5 wurde ergänzt, dass die Einflüsse von nicht oder nur einseitig bearbeiteten Schweißnähten auf die Ermüdungsfestigkeit im Rahmen von Ermüdungsanalysen zu berücksichtigen sind.

Zu Abschnitt 8.2 "Behälter"

Da eine Dimensionierung von Stutzen für Innendruck nicht zwingend nach den Gleichungen des Anhangs a 2.7 erfolgen muss, wurde die Formulierung in Abschnitt 8.2.1.2 entsprechend präzisiert.

Zu Abschnitt 8.3 "Armaturengehäuse"

(1) An mehreren Stellen wurden klarstellende Präzisierungen der Formulierungen und eine Anpassung der Gleichungen an die in den Bildern dargestellten Angaben vorgenommen.

(2) Die Änderungen in Abschnitt 8.3.3 (4) und in Bild 8.3-1 (Teilbild b) stellen eine Verschärfung gegenüber dem ASME Code dar. Sie werden für erforderlich gehalten, da die tragende Fläche des Flanschblattes nicht sowohl bei der Dimensionierung des Gehäuses als auch bei der Dimensionierung des Flansches herangezogen werden kann.

(3) Nach Auswertung der Erfahrungen bei der Anwendung der KTA 3201.2 (1996-06) wurde festgestellt, dass die Anwendung der pauschalen Spannungsanalyse auch für Eckventile zugelassen werden kann, sofern keine wesentliche gegenseitige Beeinflussung der Stutzen vorliegt. Nach vorliegenden Erfahrungen aus der Auswertung von Finite-Elemente-Berechnungen ist die gegenseitige Beeinflussung bei prismatischen Gehäusen gering. Die Anforderung in Abschnitt 8.3.4 (8) wurde entsprechend ergänzt.

(4) Da in der Stufe 0 nur eine Bewertung der primären Membranspannung erfolgt, wurde in Abschnitt 8.3.4 (2) und in Tabelle 8.3-2 die Anforderung für die Stufe 0 gestrichen.

Zu Abschnitt 8.4 "Rohrleitungen"

(1) Mit den Anforderungen in Abschnitt 8.4.1 (7) und in Bild 8.4-1 wurden Regelungen für Induktivbiegungen neu aufgenommen, mit denen Wanddickenumlagerungen an Induktivbiegungen bei der komponentenspezifischen Analyse des mechanischen Verhaltens berücksichtigt werden. Die Vorgaben gelten unter der Voraussetzung, dass die Abmessungen nach KTA 3201.3 Abschnitt 6.4.3.5 (5) a) (Standardinduktivbiegungen) eingehalten werden. Bei Induktivbiegungen, die diese Vorgaben nicht einhalten, erfolgt die Berücksichtigung der Aufstauchung über die im Abschnitt 8.4.2 ergänzte Definition der Wanddicke sc.

(2) Da der Abschnitt 8.4 für Rohrleitungssysteme konzipiert ist, wurde im Abschnitt 8.4.2 klargestellt, dass der Spannungsbeiwert bei einer - eigentlich nicht vorgesehenen - Anwendung der Gleichung (8.4-1) auf ein einzelnes gerades Rohr zu modifizieren ist.

(3) Im Abschnitt 8.4.3.2 wurde die Forderung nach Berücksichtigung

von Momentenanteile aus Zwängungen infolge unterschiedlicher Gebäudebewegungen, die auf einen Rohrstrang wirken können,
der Belastungen infolge thermischer Schichtenströmung

neu aufgenommen. Die in der Literatur [7] enthaltene Vorgehensweise stellt ein vereinfachtes und unter Umständen sehr konservatives Verfahren dar. Sofern Kenntnisse über die vorliegenden Trennschichthöhen und -breiten vorhanden sind, ist anstelle der vereinfachten Vorgehensweise auch ein detaillierterer Nachweis möglich, bei dem sich entsprechend genauere Spannungswerte ergeben.

(4) Im Abschnitt 8.4.3.6 "Ermittlung der Temperaturschwingbreiten" wurde klargestellt, dass eine zeit- und ortsabhängige Betrachtung zugelassen ist. Im Bild 8.4-2 wurden einige Präzisierungen vorgenommen.

(5) Der Spannungsbeiwert C3 in Zeile 1 der Tabelle 8.4-1 (gerades Rohr ohne Schweißnähte oder Störstellen) wurde an die Zeile 2 (stumpfgeschweißte Umfangsnähte) angeglichen und mit dem Wert 0,6 festgelegt. Diese Festlegung erfolgte abweichend vom ASME Code und nach Rückfrage beim zuständigen ASME-Committee, da sie physikalisch zutreffend ist.

Der Spannungsbeiwert B1 für Bögen oder Biegungen wurde übereinstimmend mit dem aktuellen ASME Code festgelegt.

Die in Tabelle 8.4-1 angegebenen Korrekturfaktoren für die B2-Beiwerte für Rohrleitungen mit 50 < da/sc 5.100 wurden dem ASME Code, NB-3683.2c) entnommen und beheben den bisherigen Mangel, dass für dünnwandige Rohrleitungen mit da/sc > 50 bisher keine B2-Beiwerte verfügbar waren. Diese Korrekturen berücksichtigen das im Vergleich zu Rohrleitungen mit da/sc 5 50 andere Versagensverhalten dünnwandiger Rohrleitungen mit da/sc > 50. Zahlreiche experimentelle und theoretische Untersuchungen zeigen, dass Rohre mit d_a/s_c < 30 das plastische Moment erreichen, wobei ein großes plastisches Plateau in den Momenten-Verdrehungs-Verläufen und nur kleine Ovalisierungen auftreten. Die Rohre versagen letztlich mit einem glatten Knick. Bei d_a/s_c-Verhältnissen zwischen 30 und 70 treten erhebliche Ovalisierungen und eine geringe Plastifizierung auf. Im Bereich d_a/s_c> 70 versagen die Rohre durch Beulen mit mehreren Falten vor Erreichen der Streckgrenze.

(6) Im Abschnitt 8.4.8.1 wurde klargestellt, dass die Vergleichsspannungen gemäß den Tabellen 7.7-4 bis 7.7-6 zu begrenzen sind.

(7) Im Abschnitt 8.4.8.2 wurde ergänzt, dass die Anwendbarkeit der Spannungsbeiwerte auf Biegungen mit Wanddickenaufstauchungen größer als 15 %, bezogen auf die Nennwanddicke, (Induktivbiegungen) im Einzelfall nachzuweisen ist. Es ist vorgesehen, die Anwendbarkeit der Spannungsbeiwerte auf Induktivbiegungen durch Vergleichsrechnungen zu prüfen und auf dieser Basis eine Präzisierung der Anforderung vorzunehmen.

(8) Im Abschnitt 8.4.9 "Flexibilitäts- und Spannungserhöhungsfaktoren" wurden folgende Änderungen vorgenommen:

Die Flexibilitätsfaktoren für Bögen und Biegungen wurden durch eine Regelung für den Fall ergänzt, dass Flansche oder ähnliche Versteifungen in einer Entfernung LG kleiner als oder gleich d_m/2 vom Krümmungsanfang oder -ende vorhanden sind. Diese Regelung wurde aus KTA 3211.2 Tabelle 8.5-5 Fußnote 5 übernommen.
Um die nach der bisherigen Regelung in einigen Fällen (in den Übergangsbereiche der Gleichungen zur Ermittlung der K-Faktoren) auftretenden großen Sprünge in den K-Faktoren zu vermeiden, wurde nach Auswertung umfangreicher Finite-Elemente-Analysen festgelegt, die K-Faktoren für die Übergangsbereiche durch lineare Interpolation zu ermitteln.
Die Primärspannungen dürfen nicht unter dem Wert des geraden ungestörten Rohres liegen. Bei kleinen Spannungsbeiwerten C2m kann durch den Faktor 0,67 eine geringere Spannung als im geraden Rohr errechnet werden. Deshalb wurden die Gleichungen 8.4-83 und 8.4-84 so ergänzt, dass mindestens der Wert 1,0 · M_iIzu verwenden ist.

Zu Abschnitt a 2.5 "Gewölbte Böden"

Der Abschnitt a 2.5.2.3 (2) wurde zusammen mit dem Bild a 2.5-5 gestrichen, da das aus dem früheren AD Merkblatt B3 entnommene Nachweisverfahren sich als nicht geeignet erwiesen hat und im Anwendungsbereich der KTA 3201.2 mit s_0n/d_ak 0,001 ein elastisches Einbeulen in der Krempe unter Innendruckbelastung nicht zu erwarten ist (vergleiche H. Hey: Stabilitätsfragen bei Krempen, TÜ 1988-12, S. 408-413). Dementsprechend ist diese Nachweisforderung inzwischen auch in AD B3 nicht mehr enthalten.

Zu den Abschnitten a 2.8 "Schraubenverbindungen" und a 2.9 "Flansche"

(1) Die Abschnitte a 2.8 und a 2.9 wurden zur Anpassung an den aktuellen Kenntnisstand ergänzt um

Festlegungen zur Berechnung von Flanschverbindungen mit Dichtungen im Kraftnebenschluss,
Flussdiagramme, in denen die prinzipielle Vorgehensweise bei der Nachweisführung für Dichtungen im Krafthaupt- und im Kraftnebenschluss dargestellt ist.

Hierbei handelt es sich nicht um grundsätzlich neue Vorgehensweisen, sondern um die Einarbeitung der bisher üblichen Praxis unter Berücksichtigung der aktuellen DIN-EN-Normen.

(2) In den Abschnitten a 2.8.3 und a 2.9.2 "Allgemeines" sind die erforderlichen Nachweisschritte entsprechend der Darstellung in den neu aufgenommenen Flussdiagrammen benannt.

Die Festlegung der für die verschiedenen Nachweisschritte zugrunde zu legenden Schraubenkräfte im Abschnitt a 2.8.3 (3) dient der erforderlichen Nachweissicherheit. Bei Kraftnebenschlussverbindungen berücksichtigen die Festlegungen, dass bei einer Schraubenzahl größer oder gleich 8 ein gleichmäßigeres Verformungsverhalten des Flanschblatts vorliegt.

(3) In Auswertung des VDI Berichtes 1903 "Schraubenverbindungen; Berechnung, Gestaltung, Anwendung" (VDI-Verlag, Dresden 2005) wurde in Abschnitt a 2.8.3 alternativ die Nachweisführung nach VDI 2230 zugelassen und eine Anpassung der Gleichungen in Abschnitt a 2.8.4.5.2 vorgenommen, so dass zu den aktuellen Anforderungen nach VDI 2230 kein Widerspruch besteht. Als Folge der Anpassung an das Vorgehen nach VDI 2230 konnte die Berechnung der Gesamteinschraubtiefe unter Berücksichtigung der Gewindeaussenkung (Abschnitt a 2.8.4.3.5 in der Regelfassung 1996-06) entfallen.

(4) In den Gleichungen a 2.8-1, a 2.8-5, a 2.8-10, a 2.8-11 und a 2.8-16 sowie a 2.9-1 wurde der Sicherheitsbeiwert für die Dichtung SD so entnommen bzw. zugefügt, dass dieser an der jeweils konkret zugehörigen Schraubenkraft berücksichtigt wird (Klarstellung, keine inhaltliche Änderung).

(5) In Gleichung a 2.8-9 ist die Abfrage nach der maximalen Kraft aus dem Rohrbiegemoment entfallen, da für die Abtragbarkeit von Reibkräften zur Aufnahme von Torsionsmomenten die Reibwirkung an der Dichtung maßgebend ist und somit der Dichtungsdurchmesser d_Dwirksam wird.

(6) Der Abschnitt a 2.8.4.1 d) "Vorspannen von Schraubenverbindungen" ist entfallen, da er inhaltlich im Abschnitt a 2.8.3.1 in den wesentlichen Punkten an übergeordneter Stelle aufgenommen ist.

(7) In den Gleichungen A.2.8-23, a 2.8-24 und a 2.8-25 zur Ermittlung der Schraubenkräfte bei Kraftnebenschlussverbindungen für das Einhalten der Blocklage im Betriebszustand wird zugrunde gelegt, dass die Reibkräfte über die metallische Auflage zwischen Dichtungs- und Flanschrand abgetragen werden, wobei konservativ eine linear angenommene Zunahme der Reibkraft von der Dichtung zum Flanschrand hin, die sich aus der Verdrehung der Flansche ergibt, berücksichtigt wird.

(8) Gleichung a 2.8-27 zur Ermittlung der Schraubenkraft bei Kraftnebenschlussverbindungen für das Erreichen der Blocklage im Einbauzustand wurde so ergänzt, dass auch Reibkräfte zur Abtragung von Torsionsmomenten und Querkräften berücksichtigt werden.

(9) Im Abschnitt a 2.8.4.5.1 (3) wurde neu aufgenommen, dass bei der Ermittlung der erforderlichen Einschraubtiefe die tatsächliche Schraubenkraft anstelle der auf die Zugfestigkeit bezogenen Schraubenkraft verwendet werden darf. Diese Regelung kann z.B. bei Sanierungsmaßnahmen zur Anwendung kommen, wenn Schrauben mit größerem Gewindedurchmesser eingesetzt werden.

(10) Für die Scherfestigkeit wird einheitlich der Wert "0,6" verwendet. In den Gleichungen a 2.8-36, a 2.8-37 und a 2.8-39 wurde der bisher verwendete Wert "0,55" in "0,6" geändert und damit an die Gleichungen a 2.8-34 und a 2.8-35 angepasst.

(11) In den Bildern a 2.9-3, a 2.9-5 und a 2.9-6 wurde die Einleitung der Schraubenkraft in Übereinstimmung mit dem konventionellen Regelwerk dargestellt. Durch die geänderte Krafteinleitung wurde in Verbindung mit den konstruktiven Anforderungen in Abschnitt 5.2.4.1 eine konservative Festlegung getroffen.

(12) Zur Dimensionierung der Flanschverbindung mit Kraftnebenschluss wurde Gleichung a 2.9-46 neu aufgenommen. Sie dient zur Bestimmung der zulässigen Flanschdrehung, mit der eine ausreichende Dichtheit der Flanschverbindung erreicht wird. Maßgebend ist dabei der Rückfederungsspalt an der Dichtung ðs1,2, der abhängig von der verwendeten Dichtung aus den Normen bzw. den Angaben des Dichtungsherstellers zu verwenden ist. Entsprechende Angaben sind zur Verfügung entsprechend Formblatt a 2.10-2.

Die Nachweise sind für den Einbauzustand, normalen und anormalen Betrieb sowie den Prüfzustand zu führen.

(13) Die Dichtheits- und Festigkeitsnachweise für Flanschverbindungen mit Kraftnebenschluss wurden auf der Grundlage der Nachweise für Krafthauptschlussverbindungen ergänzt. Der neu eingeführte Berechnungsalgorithmus basiert im Wesentlichen auf dem Berechungsmodell, das auch der Nachweisführung für Krafthauptschlussverbindungen zugrunde liegt. Hierbei werden die Flansche als Stülpkörper bzw. lineare Drehfedern und die Schrauben als Längsfedern idealisiert. Der Drehpunkt der miteinander verschraubten Flansche verlagert sich bei Kraftnebenschlussverbindungen bei der Montage nach dem Erreichen der Blocklage in die Auflagefläche der beiden Flansche. Die sich belastungsabhängig einstellenden Flanschverdrehungen bewirken im Dichtungsbereich eine Spaltvergrößerung, die durch die Dichtungsrückfederung - bei einer linearelastisch idealisierten Federkennlinie der Dichtung - ausgeglichen werden muss. Die neben der Dichtungskraft wirksame Kontaktkraft an der Auflagefläche stellt gegenüber dem mechanischen Verhalten der Gesamtverbindung bei Krafthauptschlussverbindungen eine Erweiterung dar, die in der Herleitung des neu eingeführten Algorithmus berücksichtigt wurde. Auf der Grundlage dieses Algorithmus kann analog zu den Nachweisführungen für Krafthauptschlussverbindungen für den Einbau- und Betriebszustand eine Nachprüfung der Kraft- und Verformungsverhältnisse erfolgen. Die Spaltöffnung infolge der sich gegenseitig verdrehenden Flanschblätter kann für den Einbau- und den Betriebszustand ermittelt und auf der Grundlage des Dichtungsdatenblattes bewertet werden.

(14) In den Abschnitt a 2.9.6.2.2.2 wurde die in DIN 2505 (Entwurf, Fassung April 1990) enthaltene Abgrenzung zwischen Flanschen mit kegeligem Ansatz und Flanschen ohne kegeligen Ansatz aufgenommen.

(15) Die Tabelle a 2.9-1 wurde so geändert, dass der Einbauzustand als separate Spalte erscheint und eine Angabe von zulässigen Spannungen für die Beanspruchungsstufe P nur im Prüfzustand erfolgt. Gleichzeitig wurde der Faktor K angepasst entsprechend der Formel in der DIN EN 1591, aus der der Faktor entnommen ist. Zusätzlich wurden die im Rahmen der verschiedenen Nachweisschritte zugrunde zu legenden Schraubenkräfte präzisiert.

(16) Weitere Ausführungen zu den Kraft- und Verformungsverhältnissen bei Flanschverbindungen mit Dichtungen im Kraftnebenschluss finden sich z.B. in den Arbeiten [1] bis [3].

[1]	G. Müller: Überprüfung der Kraft- und Verformungsverhältnisse bei Flanschverbindungen mit Dichtungen im Kraftnebenschluss, Dichtungstechnik, Ausgabe 01/2011, Vulkan-Verlag Essen
[2]	G. Müller: Vereinfachtes rechnerisches Verfahren zur Überprüfung der Kraft- und Verformungsverhältnisse bei Flanschverbindungen mit Dichtungen im Kraftnebenschluss, Sonderdruck, März 2011, TÜV NORD EnSys Hannover GmbH & Co. KG
[3]	Forschungsbericht "Experimentelle Ermittlung der zulässigen Belastungen von Rohrleitungsflanschverbindungen DN100 mit der Dichtung im Kraftnebenschluss (KNS)", SA-AT 19/08, Dezember 2010, Materialprüfungsanstalt Universität Stuttgart

Zu Abschnitt a 2.10 "Dichtungen"

(1) Der Abschnitt a 2.10 "Dichtungen" wurde grundlegend überarbeitet und an den aktuellen Kenntnistand angepasst. Es wurde für sinnvoll erachtet, auf eine Verwendung der nach DIN 28090-1 (1995-09) "Statische Dichtungen für Flanschverbindungen - Teil 1: Dichtungskennwerte und Prüfverfahren" ermittelten Dichtungskennwerte überzugehen. Es wird davon ausgegangen, dass künftig eine Kennwertzusammenstellung entsprechend den vorgegebenen Formblättern bereitgestellt wird.

(2) Die Kennwertdefinitionen für Dichtungen im Krafthauptschluss wurden aus DIN 28090-1 (1995-09) übernommen.

(3) Die bisherige Tabelle a 2.10-1 wurde gestrichen und durch ein Muster für eine Kennwertzusammenstellung ersetzt (Formblätter a 2.10-1 und a 2.10-2).

(4) Weitere Ausführungen zur Anwendung des Abschnitts a 2.10 finden sich z.B. in den Arbeiten [1] bis [5].

[1]	H. Kockelmann, J. Bartonicek, E. Roos: Characteristics of gaskets for bolted flanged connections - present state of the art, The 1998 ASME/JSME Joint Pressure Vessel and Piping Conference, San Diego, California; July 26-30, 1998, PVP-Vol. 367, pp. 1/10
[2]	H. Kockelmann: Leckageraten von Dichtungen für Flanschverbindungen, Rohrleitungstechnik, 7. Ausgabe (1998), S. 194/216, Vulkan-Verlag Essen
[3]	H. Kockelmann, R. Hahn, J. Bartonicek, H. Golub, M. Trobitz, F. Schöckle: Kennwerte von Dichtungen für Flanschverbindungen, 25. MPA-Seminar, 7. und 8. Oktober 1999, Stuttgart
[4]	H. Kockelmann, J. Bartonicek, R. Hahn, M. Schaaf: Design of Bolted Flanged Connections of Metalto-Metal Contact type, ASME PVP Conference 2000, July 23-27, 2000, Seattle, USA
[5]	H. Kockelmann, Y. Birembaut: Asbestos Free Materials for Gaskets for Bolted Flanged Connections, Synthesis Report of the Brite Euram Project BE 5191 Focusing on Gasket Factors and Associated Gasket Testing Procedures, 4th International Symposium on Fluid Sealing, 17-19 Septembre 1996, Mandelieu/France

Zu Abschnitt a 3 "Armaturen"

Die Gleichung a 3.1-23 wurde an die entsprechende Gleichung in DIN EN 12516-2 angepasst.

Zu Anhang B "Anforderungen an den Primärspannungsnachweis bei erneuten rechnerischen Nachweisen"

(1) In der Praxis werden die für den Neubau von Komponenten geltenden KTA-Regeln 3201.2 und 3211.2 auch für bestehende, bereits rechnerisch nachgewiesene Komponenten angewandt, um die Einhaltung der gemäß dem Stand von Wissenschaft und Technik erforderlichen Schadensvorsorge zeigen zu können. Die Notwendigkeit zur Durchführung von erneuten rechnerischen Nachweisen ergibt sich beispielsweise, wenn

sich die bestehende Komponente im Auswirkungsbereich von Austauschmaßnahmen befindet und die Zulässigkeit von geänderten Anschlusslasten, z.B. infolge des geänderten Eigengewichts der ausgetauschten Komponente, nachzuweisen ist,
an der bestehenden Komponente Beschleifungsmaßnahmen (z.B. zur Herstellung der Prüffähigkeit für wiederkehrende Prüfungen) durchgeführt worden sind, die eine Wanddickenunterschreitung zur Folge hatten,
sich neue Erkenntnisse zu den nachzuweisenden Lasten oder der gegebenen Beanspruchbarkeit der nachzuweisenden Komponente ergeben haben.

(2) Erforderliche Anpassungen gegenüber dem Stand der Genehmigung, die sich aufgrund von aktualisierten Anforderungen aus dem Stand von Wissenschaft und Technik bezüglich des Nachweises "Analyse des mechanischen Verhaltens" ergeben, sind in der Praxis durch begrenzte Anlagen-Änderungen meist relativ einfach vorzunehmen (z.B. Optimierung des Halterungssystems oder Anpassungen der Fahrweise oder Wasserchemie). Dagegen sind Anpassungen aus aktualisierten Anforderungen an die Konstruktion und an die Dimensionierung von Komponenten meist nur durch einen Komplett-Austausch der betroffenen Komponenten möglich.

(3) Mit der Dimensionierung gemäß Abschnitt 6 (Anforderungen der Stufe 0) werden die Mindestanforderungen an die Abmessungen der Bauteile festgelegt, darüber hinausgehende Anforderungen an die Abmessungen können sich aus Einwirkungen der Beanspruchungsstufen A, B, C, D oder P ergeben. Mit der Stufe 0 ist es im Rahmen der Errichtung einer Anlage möglich, die insgesamt erforderlichen Festigkeitsnachweise zeitlich zu staffeln. In einem ersten Schritt erfolgt mit den Daten der Stufe 0 und P die Komponentendimensionierung, die im Allgemeinen Voraussetzung für die Fertigungsfreigabe ist. In einem zweiten Schritt ist die Spannungsanalyse mit den Daten der Stufen A, B, C und D durchzuführen, die bis zur Druckprüfung vorliegen sollte. Zur Vereinfachung und Minimierung des rechnerischen Aufwandes werden in den Stufen A, B, C und D im Regelfall nur die Längsspannungen betrachtet. Die Umfangsspannungen werden bereits in der Stufe 0 begrenzt.

(4) Vor dem Hintergrund, dass in der Praxis der Dimensionierungs-Schritt im Rahmen der Errichtung mit Konservativitäten erfolgt, die u. a. auch Planungsunsicherheiten bei der Anlagenerrichtung abdecken sollen, müssen die Dimensionierungs-Anforderungen gemäß Abschnitt 6 bei erneuten Primärspannungsnachweisen nicht unbedingt erfüllt sein, um eine ausreichende Schadensvorsorge gemäß dem Stand von Wissenschaft und Technik zu gewährleisten. Deshalb sind bei erneuten rechnerischen Nachweisen, bei denen die Planungsunsicherheiten der Erstauslegung der Anlage nicht mehr gegeben sind, andere Wege zulässig, die ausreichende Dimensionierung nachzuweisen. D. h., der Primärspannungsnachweis kann unter Würdigung des Kenntnisstandes zum Nachweiszeitpunkt in der im Anhang B beschriebenen Weise erfolgen, um die geforderte ausreichende Schadensvorsorge gemäß dem Stand von Wissenschaft und Technik nachzuweisen. Hierbei wird berücksichtigt, dass Auslegungsdruck und -temperatur abdeckend für die Stufe a sein müssen, dass die Lasten der Stufe 0 und a im Grenzfall also identisch sein dürfen. Diese Bedingung stimmt inhaltlich mit den Festlegungen im aktuellen ASME BPVC 2010, Section III, Division 1, Subsection NC, Article NC-3112 und Subsection NCA, Article 2142.1 überein. Somit ist aus dem Regelwerk keine zusätzliche Sicherheit durch die Anwendung der Stufe 0 im Vergleich zur Anwendung der Stufe a quantifizierbar.

(5) Um entsprechende Bewertungsmaßstäbe zur Verfügung zu stellen, wurden qualitative und methodische Anforderungen an den Primärspannungsnachweis bei erneuten rechnerischen Nachweisen als Anhang B neu aufgenommen.

Zu Anhang D "Verfahren zur Sprödbruchanalyse"

Der bisherige Abschnitt D 2 "Berechnungsverfahren zur Ermittlung der KI-Werte" wurde gestrichen, da er nicht der in Deutschland entsprechend dem Stand von Wissenschaft und Technik üblichen Nachweisführung entspricht, die auf Finite-Elemente-Berechnungen basiert. Er entspricht außerdem nicht dem inzwischen weiter fortgeschriebenen Stand des ASME Code Section XI "Inservices Inspection", aus dem er übernommen wurde, und ist auch nicht geeignet, den Einfluss der Plattierung zu berücksichtigen, wie dies in KTA 3201.2 gefordert ist. Gleichzeitig wurden als neuer Abschnitt D 2 Festlegungen zur Ermittlung der Bruchzähigkeit nach Warmvorbelastung aufgenommen, siehe hierzu auch die Erläuterungen zu Abschnitt 7.9.

ENDE

umwelt-online - Demo-Version

(Stand: 26.01.2021)

Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: ab 105.- € netto

(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)

Preise & Bestellung

Die Zugangskennung wird kurzfristig übermittelt

? Fragen ?
Abonnentenzugang/Volltextversion