
| zurück |  |
Bild 8.4-6: Bezeichnung der Momente am Abzweig
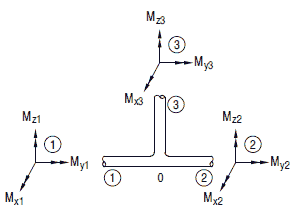
(3) Für Abzweige sind die Terme für Mi in den Gleichungen (8.4-1), (8.4-2), (8.4-3), (8.4-4) und (8.4-6) wie folgt zu ersetzen:
|
(8.4-40) |
|
(8.4-41) |
|
(8.4-42) |
worin
Za= π / 4 dRm 2 · sRc
ZH= π / 4 dHm 2 · sHc
sind.
(4) Für Abzweige nach Abschnitt a 2.7 sind dRm, sRc, dHmund sHcin Bild 8.4-7 angegeben.
Bild 8.4-7 Stutzenabmessungen
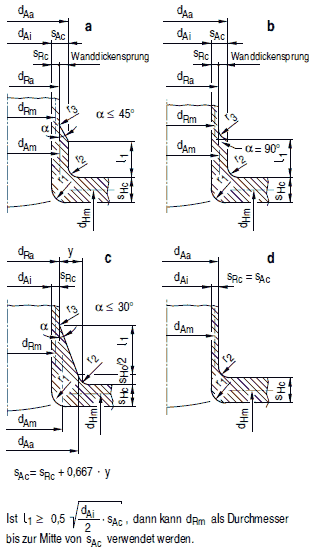
Bezeichnungen zum Bild 8.4-7
| Formelzeichen | Berechnungsgröße | Einheit |
| dAa | Außendurchmesser des Abzweiges | mm |
| dAi | Innendurchmesser des Abzweiges | mm |
| dAm | mittlerer Durchmesser des Abzweiges | mm |
| dHm | mittlerer Durchmesser der Hauptleitung | mm |
| dRa | Außendurchmesser des Abzweigrohres | mm |
| dRi | Innendurchmesser des Abzweigrohres | mm |
| dRm | mittlerer Durchmesser des Abzweigrohres | mm |
| sAc | Wanddicke des Abzweiges | mm |
| sHc | Wanddicke der Hauptleitung | mm |
| sRc | Wanddicke des Abzweigrohres | mm |
| r1, r2, r3, y | (siehe Bild) | |
| α | Neigungswinkel | Grad |
8.4.7.3.6.2 Spannungsbeiwerte für Abzweige nach Abschnitt a 2.7
(1) Voraussetzungen für die Anwendbarkeit
Die angegebenen Spannungsbeiwerte gelten für Abzweiganschlüsse, wenn die nachfolgenden Bedingungen a) bis h) erfüllt sind:
(2) Spannungsbeiwerte für Primärspannungen
| B2a= 0,5 · C2a> 1,0 | (8.4-43) |
| B2H= 0,75 · C2H> 1,0 | (8.4-44) |
(3) Spannungsbeiwerte für Primär- plus Sekundärspannungen
Die Beiwerte C1, C2aund C2Hkönnen aus folgenden Beziehungen bestimmt werden:
| (8.4-45) |
jedoch nicht kleiner als 1,2.
Für r2 / sRcgrößer als 12 ist zur Bestimmung von C1 r2 / sRc= 12 zu setzen.
| (8.4-46) |
jedoch nicht kleiner als 1,5.
| (8.4-47) |
jedoch nicht kleiner als 1,5.
(4) Spannungsbeiwerte für Spitzenspannungen
Die Beiwerte K2aund K2Hfür Momentenbelastungen können wie folgt gesetzt werden:
K2a= 1,0 K2H= 1,75
wobei das Produkt K2H· C2Hgrößer als oder gleich 2,65 sein soll.
8.4.7.3.6.3 Spannungsbeiwerte für Einschweiß-T-Stücke
(1) Die in Tabelle 8.4-1 sowie die nachfolgend angegebenen Spannungsbeiwerte für Einschweiß-T-Stücke sind anwendbar, wenn diese den Anforderungen gemäß Abschnitt a 4.6.1 oder a 4.6.2 genügen.
(2) Zur Ermittlung der Spannungen aus Innendruck und Momenten sowie der Spannungsbeiwerte sind die Anschlussdurchmesser (dHa, dAa) und die äquivalenten Anschlusswanddicken (sH+, + sA+ ) gemäß Abschnitt a 4.6.1.5 oder a 4.6.2.4 zu verwenden.
(3) Spannungsbeiwerte für Primärspannungen
Die Beiwerte B2aund B2Hkönnen wie folgt bestimmt werden:
| (8.4-48) |
jedoch nicht kleiner als 1,0
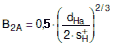 |
(8.4-49) |
jedoch nicht kleiner als 1,0
(4) Spannungsbeiwerte für Primär- plus Sekundärspannungen
Die Spannungsbeiwerte für Momentenbelastungen C2aund C2Hbetragen:
| (8.4-50) |
jedoch nicht kleiner als 2,0
| C2H = C2A | (8.4-51) |
(5) Spannungsbeiwerte für Spitzenspannungen
Die Spannungsbeiwerte für Momentenbelastungen K2aund K2Hbetragen:
| K2a= K2H= 1 | (8.4-52) |
8.4.8 Detaillierte Spannungsermittlung
8.4.8.1 Allgemeines
(1) Anstelle der Spannungsermittlung nach den Abschnitten 8.4.2 bis 8.4.5 dürfen die Spannungen gemäß diesem Abschnitt bestimmt werden.
(2) Zur Ermittlung einer Normalspannung 2 gilt mit 2N als Nennspannung und i als Spannungsbeiwert die Beziehung
σ = i · σN
Entsprechend gilt für Schubspannungen:
τ = i · τN
(3) In diesem Abschnitt gelten für die Nennspannungen folgende Definitionen:
Bei Belastung durch Innendruck p
| σN (p) = p · di / (2 · sc) | (8.4-53) |
Bei Belastung durch Biegemoment Mb
| σN (Mb) = Mb / W | (8.4-54) |
Bei Belastung durch Torsionsmoment Mt
| τN (Mt) = Mt / (2 · W) | (8.4-55) |
(4) Für die Spannungskomponenten am Rohrquerschnitt gelten entsprechend Abschnitt 8.2.2 und Bild 8.4-8 folgende Definitionen:
σa: Spannungskomponente in axialer Richtung
σt: Spannungskomponente in Umfangsrichtung
σr: Spannungskomponente in radialer Richtung
τat= τta: Schubspannungskomponenten in Umfangsrichtung und axialer Richtung
(5) Mit diesen Spannungskomponenten sind für die untersuchten Stellen die Vergleichsspannungen zu ermitteln und gemäß den Tabellen 7.7-4 bis 7.7-6 zu begrenzen.
Bild 8.4-8: Bezeichnung am Rohrbogen für detaillierte Spannungsanalyse
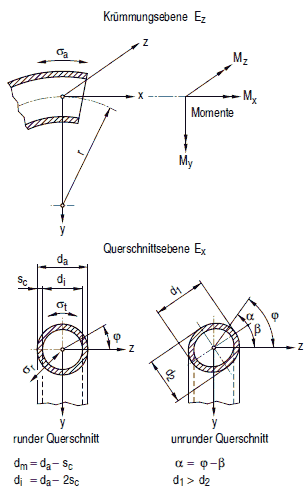
8.4.8.2 Rohrbögen und Biegungen
(1) Die Spannungsbeiwerte der Tabellen 8.4-2 und 8.4-3 gelten für Rohrbögen und Biegungen unter der Voraussetzung, dass die untersuchten Stellen ausreichend weit von Umfangsnähten, Längsnähten und anderen lokalen Störstellen entfernt sind. Anderenfalls sind zusätzliche theoretische oder experimentelle Untersuchungen erforderlich. Die Anwendbarkeit der Spannungsbeiwerte für Biegungen mit Wanddickenaufstauchungen größer als 15 %, bezogen auf die Nennwanddicke, (Induktivbiegungen) ist im Einzelfall nachzuweisen.
(2) Die bei den Spannungsbeiwerten verwendeten Bezeichnungen gehen aus Bild 8.4-8 hervor. Dabei sind die Momentenkomponenten wie folgt definiert:
Mx: Torsionsmoment
My: Biegemoment, das den Bogen aus der Krümmungsebene Ez heraus verformt
Mz: Biegemoment, das den Bogen in der Krümmungsebene Eyverformt
(3) Die in Tabelle 8.4-2 für Innendruckbelastung angeführten Spannungsbeiwerte haben folgende Größen:
|
(8.4-56) |
| i2= 0,5 · di / dm | (8.4-57) |
|
(8.4-58) |
| i4 = 2 · sc / di | (8.4-59) |
Tabelle 8.4-2: Spannungsbeiwerte für Rohrbögen unter Innendruck
| Umfangsort | Rohrwandort | Spannungsrichtung | Spannungsbeiwert |
| runder Querschnitt | |||
Φ |
außen | σt | i1 - 0,5 · i4 |
| Mitte | i1 | ||
| innen | i1 + 0,5 · i4 | ||
| jeder | außen | σa | i2 |
| Mitte | i2 | ||
| innen | i2 | ||
| unrunder Querschnitt | |||
Φ |
außen | σt | i1 - i3 - 0,5 · i4 |
| Mitte | i1 | ||
| innen | i1 + i3 + 0,5 · i4 | ||
| außen | σa | i2 - 0,3 · i3 | |
| Mitte | i2 | ||
| innen | i2 + 0,3 · i3 | ||
| runder und unrunder Querschnitt außen | |||
| jeder | außen | σr | 0 |
| Mitte | - 0,5 · i4 | ||
| innen | - i4 | ||
(4) Die in Tabelle 8.4-3 für Momentenbelastung angeführten Spannungsfaktoren haben mit
| (8.4-60) | |
| Ψ = 2 · p · r2 / (E · dm · sc) | (8.4-61) |
| x1 = 5 + 6 · λ2 + 24 · Ψ | (8.4-62) |
| x2 = 17 + 600 · λ2 + 480 · Ψ | (8.4-63) |
| x3 = x1 · x2 - 6,25 | (8.4-64) |
| x4 = (1 - v2) · (x3 - 4,5 · x2) | (8.4-65) |
die nachfolgend angeführten Größen und gelten nur bei λ> 0,2.
In die Gleichung für Ψ darf für p nicht mehr als der jeweilige Innendruck eingesetzt werden.
Für Biegemoment My gilt:
| iamy= cosΦ + [(1,5 · x2 - 18,75) · cos3Φ (+ 11,25 · cos5Φ] / x4 | (8.4-66) |
| itby= -λ · (9 · x2· sin2Φ + 225 · sin4Φ ) / x4 | (8.4-67) |
Für Biegemoment Mz gilt:
| iamz= sinΦ + [(1,5 · x2 - 18,75) · sin3Φ + 11,25 · sin5Φ] / x4 | (8.4-68) |
| itbz= λ · (9 · x2· cos2Φ + 225 · cos4Φ ) / x4 | (8.4-69) |
| itmz = -0,5 · (dm / r) · cosΦ · {cosΦ + [(0,5 · x2- 6,25) cos3Φ + 2,25 · cos5Φ ] / x4} | (8.4-70) |
(5) Für die Einstufung der mit den hier angeführten Spannungsbeiwerten ermittelten Spannungen in die Spannungskategorien entsprechend Abschnitt 7.7.2 gilt Tabelle 8.4-4.
8.4.8.3 Abzweige nach Abschnitt a 2.7
Für die Abzweige nach Abschnitt a 2.7 darf die Ermittlung der Spannungen infolge Innendruck nach Abschnitt 8.2.2.1 und der Spannungen infolge der Kräfte und Momente nach Abschnitt 8.2.2.4 erfolgen, wenn die in Abschnitt 8.2.2.1 angegebenen geometrischen Bedingungen eingehalten sind.
Tabelle 8.4-3: Spannungsbeiwerte für Rohrbögen unter Momentenbelastung
| Umfangsort | Rohrwandort | Spannungsrichtung | Spannungsbeiwert |
| für Torsionsmoment Mx | |||
| Jeder | außen | τat | 1 |
| Mitte | 1 | ||
| innen | 1 | ||
| für Biegemomente My | |||
| Φ | außen | σt | itby |
| Mitte | 0 | ||
| innen | - itby | ||
| außen | σa | iamy+ ν · itby | |
| Mitte | iamy | ||
| innen | iamy- ν · itby | ||
| für Biegemomente Mz | |||
| Φ | außen | σt | itmz+ itbz |
| Mitte | itmz | ||
| innen | itmz- itbz | ||
| außen | σa | iamz+ ν · itbz | |
| Mitte | iamz | ||
| innen | iamz- ν · itbz | ||
Tabelle 8.4-4: Spannungskategorien für Rohrbögen bei detaillierter Spannungsanalyse
| Spannungsursache | Spannungsart 1 | Spannungskategorie |
| Innendruck | Membranspannungen | Pm |
| Biegespannungen | Q | |
| Momente infolge äußerer Lasten | Membran- und Torsionsspannungen | Pl |
| 75 % der Biegespannungen | Pb | |
| 25 % der Biegespannungen | Q | |
| Momente infolge behinderter Wärmedehnung und Randpunktverschiebungen | Membran-, Biege- und Torsionsspannungen | Q |
| 1) Bezogen auf Verlauf über die Wanddicke | ||
8.4.9 Flexibilitäts- und Spannungserhöhungsfaktoren
8.4.9.1 Allgemeines
(1) Einzelne Rohrleitungselemente weisen unter Biegebeanspruchung durch Verformung des Rohrquerschnitts und dadurch bedingter Spannungserhöhung im Vergleich zum geraden Rohr eine erhöhte Flexibilität auf.
(2) Sofern die Systemanalyse für die Rohrleitung nach der Balkentheorie (gerader Balken mit Kreisringquerschnitt) durchgeführt wird, ist diesem erhöhten Verformungsverhalten durch Werte k größer als oder gleich 1 für die Flexibilitätsfaktoren und C größer als oder gleich 1 für die Spannungserhöhungsfaktoren Rechnung zu tragen.
(3) Torsionsmomente sowie Normal- und Querkräfte bewirken im Vergleich zum geraden Rohr keine erhöhte Flexibilität und keine erhöhte Beanspruchung.
8.4.9.2 Gerade Rohre
(1) Für die Ermittlung der Verformungen gerader Rohre infolge Biege- und Torsionsmomente sowie Normal- und Querkräfte gilt die Balkentheorie.
(2) Für die Analyse gerader Rohre sind alle Flexibilitätsfaktoren mit k = 1 und der Spannungserhöhungsfaktor mit C = 1 anzusetzen.
8.4.9.3 Bögen und Biegungen
(1) Für Bögen und den Krümmungsbereich von Biegungen sind die sich nach der Balkentheorie durch Biegemomente (My oder Mzentsprechend Bild 8.4-9) ergebenden Verformungen mit den Flexibilitätsfaktoren kyoder kz zu multiplizieren. Dabei kann die Systemanalyse entweder mit mittleren Werten oder mit ortsabhängigen Werten für die Flexibilitätsfaktoren durchgeführt werden.
Bild 8.4-9: Definition der Momentenrichtung
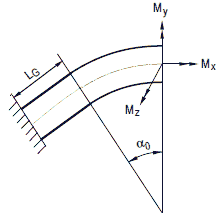
(2) Für die Ermittlung der Verformungen infolge Torsionsmomente sowie Normal- und Querkräfte gilt weiterhin die Balkentheorie.
(3) Der nachfolgende Wert für den mittleren Flexibilitätsfaktor km= ky= kzgrößer als oder gleich 1,0 gilt, sofern für die Bögen und Biegungen die folgenden Bedingungen eingehalten sind:
| km= kp · 1,65 / h; aber> 1 | (8.4-71) |
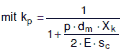 |
(8.4-72) |
| (8.4-73) | |
| h = 4 · r ·sc / dm2 | (8.4-74) |
(4) Sind Flansche oder ähnliche Versteifungen in einer Entfernung LG kleiner als oder gleich dm / 2 vom Krümmungsanfang oder -ende vorhanden, ist für derartige Bögen und Biegungen km= ky= kz= 1,0 anzusetzen oder k´ gemäß Absatz 6 zu verwenden.
(5) Sind Flansche oder ähnliche Versteifungen in einer Entfernung LG kleiner als oder gleich 2 - dm vom Krümmungsanfang oder -ende vorhanden, ist für derartige Bögen und Biegungen zwischen km= ky= kz= 1,0 oder k´ gemäß Absatz 6 und dem Ergebnis der Gleichung (8.4-71) in Abhängigkeit vom Verhältnis LG / dm linear zu interpolieren.
(6) Für k´ gilt:
k´ = c · k, jedoch k´> 1,
wobei
c = h 1/ 6bei einseitiger Versteifung;
c = h 1/ 3bei beidseitiger Versteifung.
(7) Bei Systemanalysen mit mittleren Flexibilitätsfaktoren sind die mittleren Spannungsbeiwerte C2 entsprechend Abschnitt 8.4.7.3.5 zu verwenden.
(8) Bei der Spannungsanalyse wird in den Gleichungen (8.4-1) bis (8.4-6) die Biegespannung aus einem resultierenden Moment infolge der Biege- und Torsionsmomente mit dem mittleren Spannungsbeiwert ermittelt.
(9) Die nachfolgenden Werte für die ortsabhängigen Flexibilitätsfaktoren kx ≠ ky ≠ kzgelten für die Bögen und Biegungen, die an beiden Enden gerade Rohre mit der Abmessung des Bogens aufweisen, und deren Abstand zum nächsten Bogen mindestens zweimal den Außendurchmesser beträgt:
| kx= 1,0 | (8.4-75) |
| ky= kp· 1,25 / h; aber> 1, | (8.4-76) |
| kz= kp· ka / h; aber> 1, | (8.4-77) |
mit
kpentsprechend Gleichung (8.4-72)
h entsprechend Gleichung (8.4-74)
kα= 1,65 für α0 e 180°
kα = 1,30 für α0 = 90°
kα = 1,10 für α0 = 45°
kα = h für α0 = 0°
Die Werte für kzdürfen im Bereich zwischen 180° und 0° linear interpoliert werden.
(10) Bei Systemanalysen mit ortsabhängigen Flexibilitätsfaktoren dürfen nachfolgende orts- und momentabhängige Spannungsbeiwerte C2mverwendet werden:
| C2x = 1,0 | (8.4-78) |
| C2y= 1,71 / h0,53aber> 1 | (8.4-79) |
| C2z = 1,95 / h2 / 3für α0> 90° | (8.4-80) |
| = 1,75 / h0,58für α0 = 45° | (8.4-81) |
| = 1,0 für α0= 0° | (8.4-82) |
Die Werte für C2zdürfen im Bereich zwischen 90° und 0° linear interpoliert werden, jedoch darf kein Wert mit α0kleiner als 30° verwendet werden; C2zist immer größer als oder gleich 1 anzusetzen.
(11) Sind Flansche oder ähnliche Versteifungen in einer Entfernung LGkleiner als oder gleich 2 · da vom Krümmungsanfang oder -ende vorhanden, ist für derartige Bögen und Biegungen zwischen ky und kzder Gleichungen (8.4-76) und (8.4-77) und k"y,zgemäß Absatz 12 in Abhängigkeit vom Verhältnis LG / dalinear zu interpolieren.
(12) Rohrbögen und Biegungen, bei denen in einer Entfernung LGkleiner als oder gleich da / 2 vom Krümmungsanfang oder -ende Flansche oder ähnliche Versteifungen vorhanden sind, müssen ky durch k"y und kz durch k"zersetzt werden, wobei gilt:
k"y= c · ky, aber> 1
k"z= c · kz, aber> 1,
mit c = h 1/6bei einseitiger Versteifung und
c = h 1/3 bei beidseitiger Versteifung.
(13) Bei der Systemanalyse mit ortsabhängigen Flexibilitätsfaktoren darf bei der Spannungsanalyse in den Gleichungen (8.4-1) bis (8.4-6) die Biegespannung aus den Biege- und Torsionsmomenten mit den orts- und momentabhängigen Spannungsbeiwerten ermittelt werden. Hierzu sind die resultierenden Größen wie folgt zu ersetzen:
| - statt B2· MiInunmehr
|
(8.4-83) |
| (8.4-84) |
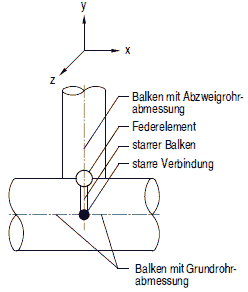
(1) Das Verformungsverhalten von Abzweigen nach Abschnitt a 2.7 kann entsprechend Bild 8.4-10 mit folgendem Modell erfasst werden:
(2) Die Steifigkeiten (Momenteneinheit pro rad) des Federelementes bezüglich der Abzweigbiegemomente können näherungsweise wie folgt angesetzt werden:
a) für Biegung um die x-Achse
| Cx = E · IR / kx · dRa | (8.4-85) |
| (8.4-86) |
b) für Biegung um die z-Achse
| Cz = E · IR / kz · dRa
mit |
(8.4-87) |
| (8.4-88) |
Für die Bezeichnungen gilt Bild 8.4-7 mit den zusätzlichen Definitionen
IR: Trägheitsmoment des abzweigenden Rohres,
| IR= π · (dRa4 - dRi4) / 64 | (8.4-89) |
sn: Rechenwert für Stutzenwanddicke, und zwar:
für Ausführung a und b von Bild 8.4-7:
sn= sAc, wenn L1> 0,5 · ((dAi + sA) · sA)0,5
sn= sRc, wenn L1 < 0,5 · ((dAi + sA) · sA)0,5
für Ausführung c von Bild 8.4-7:
sn= sRc+ (2 / 3) · y, wenn α< 30°
sn= sRc+ 0,385 · L1, wenn α > 30°
für Ausführung d von Bild 8.4-7: sn= sRc
(3) Bezüglich der Torsions-, Normal- und Querkraftverformung ist das Federelement als starr zu betrachten.
8.4.9.5 Abzweige mit dAi / dHi> 0,5 und Einschweiß-T-Stücke
Abzweige mit dAi / dHigrößer als 0,5 und Einschweiß-T-Stücke sind ebenfalls nach Abschnitt 8.4.9.4 und Bild 8.4-10 zu modellieren, jedoch unter Wegfall des Federelementes.
Bild 8.4-10: Modellierung von Abzweigen
8.5 Komponentenstützkonstruktionen
8.5.1 Komponentenstützkonstruktionen mit integralen Anschlüssen
8.5.1.1 Allgemeines
Dieser Abschnitt gilt für die Berechnung der integralen Bereiche von Komponentenstützkonstruktionen.
Komponentenstützkonstruktionen sind Konstruktionen zur Lastabtragung. Die integralen Bereiche von Komponentenstützkonstruktionen sind an die druckführende Fläche angeschweißt, angeschmiedet, angegossen oder aus dem Vollen gearbeitet. Deshalb steht der unmittelbar an die Wand der Komponente angrenzende Teil der Komponentenstützkonstruktion in Wechselwirkung mit der Komponente (Einflussbereich). Für die Berechnung der Komponentenstützkonstruktion ist nicht die Innendruckbelastung maßgebend, sondern der Kraft- und Momentenverlauf.
8.5.1.2 Abgrenzung
(1) Die Abgrenzung des integralen Bereichs der Komponentenstützkonstruktionen ist im Bild 8.5-1 dargestellt. Der Abstand l wird wie folgt berechnet:
| I = 0,5 · (r · sc)0,5 | (8.5-1) |
mit
r : mittlerer Radius der Komponentenstützkonstruktionsschale sc: Dicke der Komponentenstützkonstruktionsschale gemäß Abschnitt 7.1.4
| l = 0,5 · (r2 / 2)0,5 | (8.5-2) |
mit
r : Radius der Stange oder die Hälfte der größten Querschnittsdimension des Profils
| l = 0,5 · (r · sc)0,5 | (8.5-3) |
mit
r : Hälfte der größten Abmessung eines Flansches, T-Profils, Blechs oder Rundprofils oder Hälfte der größten Schenkelbreite eines Winkelprofils
sc: Flanschdicke von Profilen oder Blechdicke gemäß Abschnitt 7.1.4
(2) Befindet sich jedoch innerhalb des Abstands l ein lösbarer Anschluss, so ist an dieser Stelle die Grenze zwischen dem integralen und nichtintegralen Bereich der Komponentenstützkonstruktion anzusetzen.
Bild 8.5-1: Anschlussarten der Komponentenstützkonstruktion und Abklingbereich

8.5.1.3 Berechnung
(1) Integrale Bereiche von Komponentenstützkonstruktionen sind als Teil der zu unterstützenden Komponente anzusehen. Es sind sämtliche gleichzeitig auftretende Belastungen zu berücksichtigen. Für die Komponentenstützkonstruktionen sind folgende Kräfte und Momente zu ermitteln:
(2) Der Einfluss der äußeren Kräfte und Momente auf die Wandung der Komponente ist nach Abschnitt 7 zu berücksichtigen.
(3) Die Beurteilung der Spannungen ist nach Abschnitt 7 vorzunehmen.
(4) Bei Druckbeanspruchung ist die Stabilität nachzuweisen.
8.5.2 Komponentenstützkonstruktionen mit nichtintegralen Anschlüssen
Komponentenstützkonstruktionen mit nichtintegralen Anschlüssen sind in KTA 3205.1 geregelt.
9 Art und Umfang der vorzulegenden Festigkeitsnachweise und zugehörige Unterlagen
(1) Für die Prüfung durch den Sachverständigen nach § 20 AtG sind folgende Festigkeitsnachweise für die Komponenten oder Bauteile des Primärkreises zu erstellen und in Form eines Berichtes einzureichen:
(2) Bei Berechnung, Bericht und Prüfung sind die einschlägigen Abschnitte der Regeln KTA 3201.1, 3201.2, 3201.3 und 3201.4 zugrunde zu legen.
(3) Jeder Bericht über eine Berechnung soll die nachfolgenden Angaben in dem Umfang enthalten, wie dies zur Prüfung der Festigkeitsnachweise notwendig ist:
| Dimensionierung | Anhang A |
a 1 Allgemeines
(1) Die nachstehenden Berechnungsregeln gelten für die Dimensionierung der Komponenten und ihrer Bauteile gemäß Abschnitt 6 unter Auslegungsdruck und zusätzlichen Auslegungslasten bei Auslegungstemperatur. Die allgemeinen Berechnungsgrößen und Berechnungseinheiten sind in Absatz (6) aufgeführt. Weitere Berechnungsgrößen und Berechnungseinheiten sind in den einzelnen Abschnitten enthalten.
(2) Der anzuwendende Spannungsvergleichswert (Sm) ist in Abhängigkeit von der Auslegungstemperatur festzulegen. Zusatzbelastungen, zum Beispiel äußere Kräfte und Momente, sind gesondert zu erfassen und zu berücksichtigen.
(3) Die Nachrechnung von den mit der Nennwanddicke sn ausgeführten Bauteilen ist innerhalb dieses Anhangs a mit der Wanddicke s0n = sn- c1- c2mit sn> s0+ c1+ c2durchzuführen. Hinsichtlich der Zuschläge gilt Abschnitt 6.4.
(4) Die Bilder dieses Anhangs berücksichtigen nicht die Zuschläge.
(5) Die in Abschnitt a 2 enthaltenen Festlegungen für allgemeine Bauteile der drucktragenden Wand sind unter Beachtung der jeweiligen Voraussetzungen auch anwendbar auf spezifische Bauteile von Armaturen gemäß Abschnitt a 3 und Rohrleitungen gemäß Abschnitt a 4, wenn dort keine anderslautenden Regelungen getroffen sind.
(6) Berechnungsgrößen und Einheiten
| Formelzeichen | Berechnungsgröße | Einheit |
| b | Breite | mm |
| d | Durchmesser | mm |
| h | Höhe | mm |
| c | Zuschlag zur Wanddicke | mm |
| l | Länge | mm |
| p | Auslegungsdruck | MPa |
| p´ | Prüfdruck | MPa |
| q | Abflachung | mm |
| r, R | Radius | mm |
| s | Wanddicke | mm |
| s0 | Rechnerisch erforderliche Wanddicke gemäß Bild 7.1-1 | mm |
| s0n | Nennwanddicke abzüglich der Zuschläge c1 und c2 gemäß Bild 7.1-1 | mm |
| sn | Nennwanddicke gemäß Bild 7.1 -1 | mm |
| v | Verschwächungsbeiwert | - |
| A | Fläche | mm2 |
| E | Elastizitätsmodul | N / mm2 |
| F | Kraft | N |
| I | Flächenträgheitsmoment | mm4 |
| M | Moment | Nmm |
| S | Sicherheitsbeiwert | - |
| Sm | Spannungsvergleichswert | N / mm2 |
| T | Temperatur | °C |
| U | Unrundheit | % |
| W | Widerstandsmoment | mm3 |
| Φ | Winkel | Grad |
| ν | Querkontraktionszahl (= 0,3 für Stahl) | - |
| σ | Spannung | N / mm2 |
| σl | Spannung in Längsrichtung | N / mm2 |
| σr | Spannung in Radialrichtung | N / mm2 |
| σu | Spannung in Umfangsrichtung | N / mm2 |
| σV | Vergleichsspannung | N / mm2 |
| τ | Schubspannung | N / mm2 |
| Zeichen | Bedeutung |
| Kopfzeiger ^ | Maximalwert, z.B. |
| Kopfzeiger |
Minimalwert, z.B. |
| Kopfzeiger- | Mittelwert, z.B. ̄σ |
| Kopfzeiger ~ | schwellend, z.B. |
| Kopfzeiger ´ | zur Druckprüfung gehörend, z.B. p´ |
| Fußzeiger | Zahlenindex, z.B. ni |
| 1 N / mm2 = 10 bar = 10,2 at = 0,102 kp / mm2= 106Pa | |
a 2 Dimensionierung von Bauteilen der drucktragenden Wand
a 2.1 Allgemeines
Die in den Abschnitten a 2.2 bis a 2.10 angegebenen Gleichungen für die Dimensionierung gelten nur zur Ermittlung der erforderlichen Wanddicke der einzelnen Bauteile unter Innen- oder Außendruck jedoch ohne Berücksichtigung des elastischen Zusammenhangs der gesamten Struktur.
a 2.2 Zylinderschalen
a 2.2.1 Berechnungsgrößen und Einheiten zu Abschnitt a 2.2
| Formelzeichen | Berechnungsgröße | Einheit |
| da | äußerer Durchmesser der Zylinderschale | mm |
| di | innerer Durchmesser der Zylinderschale | mm |
| fk | Sicherheitsbeiwert gegen elastisches Einbeulen | - |
| fv | zusätzlicher Sicherheitsbeiwert gegen plastisches Verformen | - |
| l | Beullänge | mm |
| n | Anzahl der Einbeulwellen | - |
| p | Auslegungsdruck | MPa |
| pzul. | zulässiger Druck | MPa |
| s0 | rechnerisch erforderliche Wanddicke gemäß Bild 7.1-1 | mm |
| s0n | Nennwanddicke der Schale abzüglich Zuschläge gemäß Abschnitt 6.5 | mm |
| E | Elastizitätsmodul | N / mm2 |
| Sm | Spannungsvergleichswert | N / mm2 |
| U | Unrundheit | % |
| Z | Rechengröße: Z = 0,5 ⋅p × da / l | - |
| ν | Querkontraktionszahl | - |
| σa | axiale Spannung | N / mm2 |
| ̄σV | mittlere Vergleichsspannung | N / mm2 |
a 2.2.2 Zylinderschalen unter innerem Überdruck
a 2.2.2.1 Geltungsbereich
Die nachstehende Berechnung gilt für Zylinderschalen unter innerem Überdruck, bei denen das Verhältnis da / dikleiner als oder gleich 1,7 ist. Durchmesserverhältnisse da / di kleiner als oder gleich 2 sind zulässig, wenn die Wanddicke s0n kleiner als oder gleich 80 mm ist. Die Berechnung von Ausschnittsverstärkungen in Zylinderschalen unter innerem Überdruck ist gemäß Abschnitt a 2.7 durchzuführen.
a 2.2.2.3 Berechnung
(1) Für die Berechnung der erforderlichen Wanddicke des Grundkörpers gilt:
| s0 = da ⋅ p / 2 ⋅ Sm + p | (a 2.2-1) |
| s0 = di ⋅ p / 2 ⋅ Sm - p | (a 2.2-2) |
(2) Für die Nachrechnung bei vorgegebener Wanddicke gilt:
| (a 2.2-3) |
a 2.2.3 Zylinderschalen unter äußerem Überdruck
a 2.2.3.1 Geltungsbereich
Die nachstehende Berechnung gilt für Zylinderschalen unter äußerem Überdruck, bei denen das Verhältnis da / di kleiner als oder gleich 1,7 ist.
a 2.2.3.2 Sicherheitsbeiwerte
(1) Der zusätzliche Sicherheitsbeiwert gegen plastisches Verformen ist unabhängig vom Werkstoff mit fv= 1,2 anzusetzen.
(2) Der Sicherheitsbeiwert gegen elastisches Einbeulen ist unabhängig vom Werkstoff fk = 3,0 anzusetzen. Wird ein höherer Prüfdruck als 1,3 ⋅ p gefordert, so muss fk mindestens 2,2 betragen.
a 2.2.3.3 Berechnung
a 2.2.3.3.1 Allgemeines
(1) Die Berechnung ist gegen elastisches Einbeulen und gegen plastisches Verformen gemäß den nachfolgenden Abschnitten durchzuführen. Der errechnete kleinste Wert für pzulist maßgebend.
(2) Die Beullänge ist die Länge des Mantels. Bei Behältern mit gewölbten Böden beginnt die Beullänge am Übergang vom zylindrischen Bord zur Krempe.
a 2.2.3.3.2 Berechnung gegen elastisches Einbeulen
(1) Die Berechnung erfolgt nach folgender Gleichung:
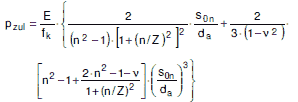 |
(a 2.2-4) |
wobei für Z = 0,5× p × da / l einzusetzen ist; n ist eine ganze Zahl und muss den Bedingungen n> 2 und n > Z genügen und ist so zu wählen, dass p zum kleinsten Wert wird. n bedeutet die Anzahl der Einbeulwellen, die beim Versagen auf dem Umfang auftreten können. Die Anzahl der Einbeulwellen darf nach folgender Näherungsgleichung abgeschätzt werden:
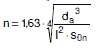 |
(a 2.2-5) |
(2) Die erforderliche Wanddicke s0n darf nach Bild a 2.2-1 für gebräuchliche Abmessungen bestimmt werden. Dieses Bild gilt für eine Querkontraktionszahl v = 0,3. Bei wesentlich anderen Querkontraktionszahlen ist nach Gleichung (a 2.2-4) zu rechnen.
a 2.2.3.3.3 Berechnung gegen plastisches Verformen
(1)
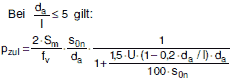 |
(a 2.2-6) |
Die erforderliche Wanddicke s0n darf nach Bild a 2.2-2 für gebräuchliche Abmessungen und mit U = 1,5 % unmittelbar bestimmt werden.
(2) Bei da / l > 5 ist der größere der nach den folgenden Gleichungen ermittelte Druck für die Festlegung des zulässigen äußeren Überdrucks maßgebend:
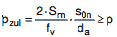 |
(a 2.2-7) |
| (a 2.2-8) |
(3) Die Gleichung (a 2.2-8) gilt hauptsächlich bei kleinen Beullängen. Die Gleichungen (a 2.2-6) bis (a 2.2-8) gelten nur dann, wenn im Zylinder keine positiven Primär-Längsspannungen σaauftreten. In den Gleichungen (a 2.2-6) bis (a 2.2-8) ist Smzu ersetzen durch (Sm - σa), wenn σa> 0 ist.
a 2.3 Kugelschalen
a 2.3.1 Berechnungsgrößen und Einheiten zu Abschnitt a 2.3
| Formelzeichen | Berechnungsgröße | Einheit |
| da | äußerer Durchmesser der Kugelschale | mm |
| di | innerer Durchmesser der Kugelschale | mm |
| dm | mittlerer Durchmesser der Kugelschale | mm |
| Ck | Berechnungsbeiwert | - |
| fk | Sicherheitsbeiwert gegen elastisches Einbeulen | - |
| fv | zusätzlicher Sicherheitsbeiwert gegen plastisches Verformen | - |
| σk | Spannung bei der Nachrechnung gegen elastisches Einbeulen | N / mm2 |
a 2.3.2 Kugelschalen unter innerem Überdruck
a 2.3.2.1 Geltungsbereich
Die nachstehende Berechnung gilt für Kugelschalen ohne Ausschnitte unter innerem Überdruck, bei denen das Verhältnis da / di< 1,5 ist. Die Berechnung von Kugelschalen mit Ausschnitten unter innerem Überdruck ist gemäß Abschnitt a 2.7 durchzuführen.
a 2.3.2.2 Berechnung
(1) Für die Berechnung der erforderlichen Wanddicke s0 für Kugelschalen mit dem Verhältnis s0n / di größer als 0,05 gelten wahlweise:
|
(a 2.3-1) |
oder
|
(a 2.3-2) |
mit
| (a 2.3-3) |
(2) Für die Berechnung der erforderlichen Wanddicke dünnwandiger Kugelschalen mit dem Verhältnis s0n / di kleiner als oder gleich 0,05 gilt:
|
(a 2.3-4) |
oder
|
(a 2.3-5) |
(3) Für die Nachrechnung bei vorgegebener Wanddicke gilt:
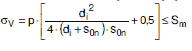 |
(a 2.3-6) |
a 2.3.3 Kugelschalen unter äußerem Überdruck a 2.3.3.1 Geltungsbereich
Die nachstehende Berechnung gilt für Kugelschalen unter äußerem Überdruck, bei denen das Verhältnis da / di kleiner als oder gleich 1,5 ist.
a 2.3.3.2 Sicherheitsbeiwerte
(1) Der zusätzliche Sicherheitsbeiwert gegen plastisches Verformen beträgt unabhängig vom Werkstoff fv = 1,2.
(2) Der Sicherheitsbeiwert gegen elastisches Einbeulen ist unabhängig vom Werkstoff der Tabelle a 2.3-1 zu entnehmen. Wird ein höherer Prüfdruck als 1,3 · p gefordert, dann ist für den Prüfdruck der Nachweis mit f´k, aus Tabelle a 2.3-1 zusätzlich zu erbringen.
Tabelle a 2.3-1: Sicherheitsbeiwerte gegen elastisches Einbeulen
| 2 ⋅ s0 / di | fk | f´k |
| 0,001 | 5,5 | 4,0 |
| 0,003 | 4,0 | 2,9 |
| 0,005 | 3,7 | 2,7 |
| 0,010 | 3,5 | 2,6 |
| > 0,1 | 3,0 | 2,2 |
| Zwischenwerte sind linear zu interpolieren. | ||
a 2.3.3.3 Berechnung
(1) Allgemeines
Die Berechnung ist gegen elastisches Einbeulen und gegen plastisches Verformen durchzuführen. Der größere sich aus den Absätzen (2) und (3) ergebende Wert für s0 ist der jeweils maßgebliche.
(2) Berechnung gegen elastisches Einbeulen
Die erforderliche Wanddicke ergibt sich aus der folgenden Gleichung
| (a 2.3-7) |
Für die Nachrechnung bei vorgegebener Wanddicke gilt:
| (a 2.3-8) |
(3) Berechnung gegen plastisches Verformen Die erforderliche Wanddicke ergibt sich aus:
| (a 2.3-9) |
Für Kugelschalen mit dem Verhältnis s0 / da ´ 0,05 darf die erforderliche Wanddicke n´herungsweise aus
|
(a 2.3-10) |
ermittelt werden.
Bei Nachrechnung mit vorgegebener Wanddicke gilt:
| (a 2.3-11) |
Bild a 2.2-1: Erforderliche Wanddicke s0nvon Zylinderschalen, Rohren und Rohrbögen bei Berechnung gegen elastisches Einbeulen
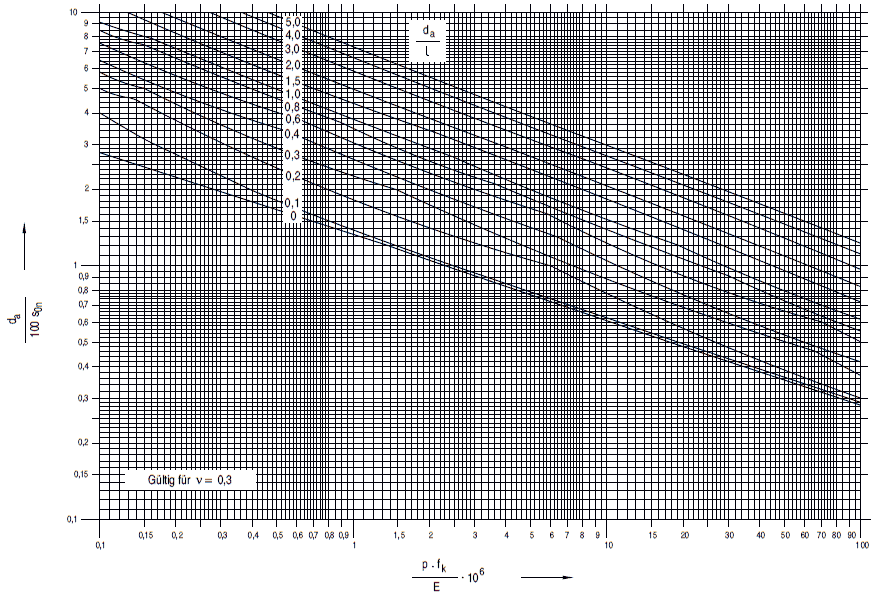
Bild a 2.2-2: Erforderliche Wanddicke s0nvon Zylinderschalen, Rohren und Rohrbögen bei Berechnung gegen plastisches Verformen
 s
s
a 2.4 Kegelschalen
a 2.4.1 Berechnungsgrößen und Einheiten zu Abschnitt a 2.4
| Formelzeichen | Berechnungsgröße | Einheit |
| da | Außendurchmesser der Kegelschale | mm |
| da1 | Außendurchmesser am weiten Ende des Kegels | mm |
| da2 | Außendurchmesser am engen Ende des Kegels | mm |
| di | Innendurchmesser der Kegelschale | mm |
| di1 | Innendurchmesser am weiten Ende des Kegels | mm |
| di2 | Innendurchmesser am engen Ende des Kegels | mm |
| e | Störbereichslänge gemäß Bild a 2.4-3 | mm |
| e1 | Störbereichslänge des weiten Teils des Kegels | mm |
| e2 | Störbereichslänge des engen Teils des Kegels | mm |
| r | Übergangsradius | mm |
| s1 | Wanddicke des weiten Teils des Kegels | mm |
| s2 | Wanddicke des engen Teils des Kegels | mm |
| Ap | drucktragende Fläche | mm2 |
| Aσ | tragende Querschnittsfläche | mm2 |
| ß | Berechnungsbeiwert gemäß Tabelle a 2.4-1 | - |
| Φ | halber Öffnungswinkel des Kegels | Grad |
| Φ1 | halber Öffnungswinkel des weiten Teils des Kegels | Grad |
| Φ2 | halber Öffnungswinkel des engen Teils des Kegels | Grad |
| ψ | absolute Differenz der halben Öffnungswinkel Φ1und Φ2 | Grad |
| σ1 | Spannung in Längsrichtung | N / mm2 |
a 2.4.2 Kegelschalen unter innerem Überdruck
a 2.4.2.1 Geltungsbereich
Die nachstehende Berechnung gilt für Kegelschalen unter innerem Überdruck ohne Ausschnitte, bei denen am weiten Ende die Bedingung 0,005< s0n / da< 0,2 eingehalten ist. Die Berechnung von Kegelschalen mit Ausschnitten unter innerem Überdruck ist gemäß Abschnitt a 2.7 durchzuführen.
Hinweis:
Dem Wert s0n / da= 0,2 entspricht für da- di= 2 · s0nder Wert da / di= 1,67.
a 2.4.2.2 Allgemeines
(1) Kegelschale mit Eckschweißungen
Kegelschalen dürfen untereinander oder mit Zylinderschalen und dergleichen ohne Krempe durch Schweißung entsprechend Abschnitt 5.3.2.6 verbunden werden.
(2) Störbereichslänge
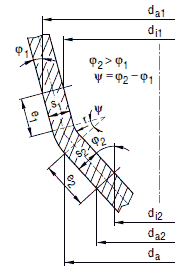
Bei Kegelschalen mit nach innen gekrümmten Übergängen muss die nach Abschnitt a 2.4.2.3 Absatz 2 oder 4 geforderte Wanddicke über dem durch die Störbereichslänge e begrenzten Krempenbereich vorhanden sein (siehe Bild a 2.4-1).
Es gilt:
| e1,e2= (r + s0n) ⋅ tan Ψ / 2 + 0,8 ⋅ (da . s0n)0,5 | (a 2.4-1) |
Bei veränderlicher Wanddicke innerhalb des Störbereichs ist für die Ermittlung der Längen e1 und e2 nach Gleichung (a 2.4-1) jeweils die Wanddicke am Auslauf der Krümmung maßgebend.
Bild a 2.4-1: Störbereichslängen e1 und e2
a 2.4.2.3 Berechnung
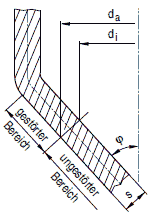
(1) Wanddickenberechnung für den ungestörten Bereich einer Kegelschale mit Φ< 70° .
Die erforderliche Wanddicke des ungestörten Bereichs einer Kegelschale (siehe Bild a 2.4-2) ergibt sich wahlweise aus:
|
(a 2.4-2) |
oder
|
(a 2.4-3) |
Für die Nachrechnung bei vorgegebener Wanddicke gilt:
| (a 2.4-4) |
Für da und di sind in den Gleichungen (a 2.4-2) bis (a 2.4-4) jeweils die Maße am weiten Ende des ungestörten Bereichs der Kegelschale einzusetzen.
Zwischen da und di besteht die Beziehung:
| di = da - 2 ⋅ s0n⋅ cos Φ | (a 2.4-5) |
Bei mehreren untereinander verbundenen kegelförmigen Mänteln mit gleichem Öffnungswinkel ist die Berechnung nach Gleichung (a 2.4-2) oder (a 2.4-3) für sämtliche Mäntel durchzuführen.
Bild a 2.4-2: Ungestörter Bereich einer Kegelschale
(2) Wanddickenberechnung für den gestörten Bereich von Kegelschalen mit nach innen gekrümmten Übergängen und Φ< 70° .
Die Bemessung erfolgt getrennt für die
Die größte sich nach a), b) und c) ergebende Wanddicke ist für die Bemessung maßgebend.
Im Hinblick auf die Umfangsspannung ist bei nach innen gekrümmten Übergängen (Bild a 2.4-1) die erforderliche Wanddicke nach Gleichung (a 2.4-2) oder (a 2.4-3) für beide Seiten des Übergangs zu ermitteln.
Hinsichtlich der Längsspannungen ergibt sich die erforderliche Wanddicke aus:
|
(a 2.4-6) |
Der Berechnungsbeiwert β ist dabei in Abhängigkeit vom Winkel Ψ und dem Verhältnis r / da der Tabelle a 2.4-1 zu entnehmen. Zwischenwerte dürfen dabei linear interpoliert werden.
Der größere Wert aus den Gleichungen (a 2.4-2) oder (a 2.4-3) und (a 2.4-6) ist maßgebend. Für die Nachrechnung bei vorgegebener Wanddicke gilt:
|
(a 2.4-7) |
Der Winkel Ψ ergibt sich aus der absoluten Differenz der halben Öffnungswinkel Φ1 und Φ2
| Ψ =ú Φ1 - Φ2ú | (a 2.4-8) |
Bei veränderlicher Wanddicke innerhalb der Abklinglänge (z.B. Schmiedestücke, Drehteile) ist für die Ermittlung der Längen e1 und e2nach Gleichung (a 2.4-1) jeweils die Wanddicke am Auslauf der Krümmung maßgebend.
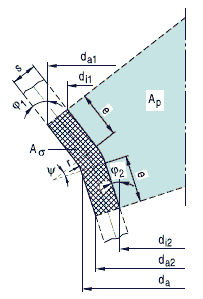
(3) Wanddickenberechnung für den gestörten Bereich von Kegelschalen mit nach außen gekrümmten Übergängen und Φ< 70° .
Bei nach außen gekrümmten Übergängen (Bild a 2.4-3) gelten grundsätzlich alle Bedingungen und Beziehungen wie bei den nach innen gekrümmten Übergängen.
Zusätzlich ist jedoch wegen der erhöhten Umfangsspannung die folgende Bedingung zu erfüllen:
| (a 2.4-9) |
(4) Wanddickenberechnung für den gestörten Bereich von flachen Kegelschalen mit Krempe und Φ > 70°
Bei sehr flachen Kegeln, deren Neigungswinkel zur Behälterachse Φ > 70° ist, darf die Bemessung nach Gleichung (a 2.4-10) erfolgen, auch wenn sich geringere Wanddicken als nach den Gleichungen (a 2.4-2), (a 2.4-3) und (a 2.4-6) ergeben:
| (a 2.4-10) |
Bild a 2.4-3: Kegelschale mit nach außen gekrümmtem Übergang
a 2.4.3 Kegelschalen unter äußerem Überdruck
Bei Beanspruchung durch äußeren Überdruck ist außer der Berechnung nach Abschnitt a 2.4.2.3 bei Kegelschalen mit ( kleiner als oder gleich 45° zusätzlich nachzuprüfen, ob der Kegel gegen elastisches Einbeulen sicher ist. Diese Nachprüfung erfolgt nach Abschnitt a 2.2.3.3.2, wobei der Kegel einem Zylinder gleichzusetzen ist, dessen Durchmesser wie folgt bestimmt wird:
|
(a 2.4-11) |
mit
da1: Durchmesser am weiten Ende des Kegels,
da2: Durchmesser am engen Ende des Kegels.
Als Länge ist dabei die axiale Länge des Kegels und der gegebenenfalls anschließenden Zylinder einzusetzen, es sei denn, dass die Zylinder am Übergang entsprechend Abschnitt a 2.2.3 ausreichend verstärkt sind.
Tabelle a 2.4-1: Berechnungsbeiwert β in Abhängigkeit vom Verhältnis r / da und Ψ
| Ψ | r / da | |||||||||||
| < 0,01 | 0,02 | 0,03 | 0,04 | 0,06 | 0,08 | 0,10 | 0,15 | 0,20 | 0,30 | 0,40 | 0,50 | |
| 0 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 |
| 10 | 1,4 | 1,3 | 1,2 | 1,2 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 |
| 20 | 2,0 | 1,8 | 1,7 | 1,6 | 1,4 | 1,3 | 1,2 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 |
| 30 | 2,7 | 2,4 | 2,2 | 2,0 | 1,8 | 1,7 | 1,6 | 1,4 | 1,3 | 1,1 | 1,1 | 1,1 |
| 45 | 4,1 | 3,7 | 3,3 | 3,0 | 2,6 | 2,4 | 2,2 | 1,9 | 1,8 | 1,4 | 1,1 | 1,1 |
| 60 | 6,4 | 5,7 | 5,1 | 4,7 | 4,0 | 3,5 | 3,2 | 2,8 | 2,5 | 2,0 | 1,4 | 1,1 |
| 70 | 10,0 | 9,0 | 8,0 | 7,2 | 6,0 | 5,3 | 4,9 | 4,2 | 3,7 | 2,7 | 1,7 | 1,1 |
| 75 | 13,6 | 11,7 | 10,7 | 9,5 | 7,7 | 7,0 | 6,3 | 5,4 | 4,8 | 3,1 | 2,0 | 1,1 |
a 2.5 Gewölbte Böden
a 2.5.1 Berechnungsgrößen und Einheiten zu Abschnitt a 2.5
| Formelzeichen | Berechnungsgröße | Einheit |
| da | Außendurchmesser eines gewölbten Bodens | mm |
| di | Innendurchmesser eines gewölbten Bodens | mm |
| dAi | Innendurchmesser eines Ausschnitts | mm |
| fk | Sicherheitsbeiwert gegen elastisches Einbeulen | - |
| f´k | Sicherheitsbeiwert gegen elastisches Einbeulen bei erhöhtem Prüfdruck | - |
| h1 | Höhe des zylindrischen Bords | mm |
| h2 | Höhe des gewölbten Bodens | mm |
| l | Abstand der Schweißnaht von der Krempe | mm |
| pB | Beuldruck | MPa |
| R | Wölbungsradius | mm |
| β | Berechnungsbeiwert | - |
a 2.5.2 Gewölbte Böden unter innerem Überdruck
a 2.5.2.1 Geltungsbereich
Die nachstehende Berechnung gilt für gewölbte Böden in Klöpper-, Korbbogen- und Halbkugelform unter innerem Überdruck, wenn folgende Beziehungen und Grenzen eingehalten sind (siehe Bild a 2.5-1):
Bild a 2.5-1: Gewölbter Boden
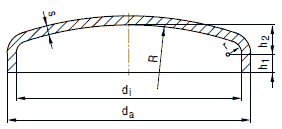
a 2.5.2.2 Allgemeines
(1) Höhe des zylindrischen Bords
Bei Klöpperböden soll die Bordhöhe grundsätzlich h1> 3,5 - s0n, bei Korbbogenböden h1> 3,0 . s0nbetragen. Sie braucht jedoch folgende Maße nicht zu überschreiten:
| Wanddicke s0nin mm | Bordhöhe h1in mm |
| s0n< 50 | 150 |
| 50 < s0n< 80 | 120 |
| 80 < s0n< 100 | 100 |
| 100 < s0n< 120 | 75 |
| 120 < s0n | 50 |
Bei Halbkugelböden ist kein zylindrischer Bord erforderlich.
(2) Wird ein gewölbter Boden aus einem Krempen- und einem Kalottenteil zusammengeschweißt, so muss die Verbindungsnaht einen ausreichenden Abstand von der Krempe haben. Als ausreichender Abstand l gilt:
a 2.5.2.3 Berechnung
Für die Berechnung der erforderlichen Wanddicke der Krempe gilt:
|
(a 2.5-1) |
Die Berechnungsbeiwerte β sind für gewölbte Böden in Klöpperform dem Bild a 2.5-3, in Korbbogenform dem Bild a 2.5-4 in Abhängigkeit von s0n / da zu entnehmen.
Ausschnitte in gewölbten Böden gemäß Bild a 2.5-2 müssen in jedem Fall den Bedingungen des Abschnitts a 2.7 genügen, wobei als Kugeldurchmesser der doppelte Wölbungsradius R einzusetzen ist. Dieses Verfahren ist jedoch bei Klöpper- und Korbbogenböden auf den Scheitelbereich von 0,6 ⋅ da zu beschränken (siehe Bild a 2.5-2).
Bild a 2.5-2: Gewölbter Boden mit Ausschnitt
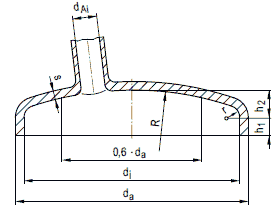
Für Vollböden in Halbkugelform gilt unabhängig von der Wanddicke im Bereich 0,5 ⋅( R ⋅ s0n)0,5 neben der Anschlussnaht der Berechnungsbeiwert β= 1,1. Bei Halbkugelböden mit Ausschnitten ist die Wanddicke der Verstärkung des Ausschnitts nach Abschnitt a 2.7 zu berechnen. Die für den Vollboden mit β = 1,1 ermittelte Wanddicke darf jedoch dabei nicht unter schritten werden.
a 2.5.3 Gewölbte Böden unter äußerem Überdruck
Für die Berechnung der erforderlichen Wanddicke der Krempe bei Beanspruchung durch äußeren Überdruck gelten die Forderungen des Abschnittes a 2.5.2 mit folgenden zusätzlichen Forderungen:
Die erforderliche Wanddicke s0 der Krempe ist aus Gleichung (a 2.5-1) zu berechnen. Bei der Berechnung der erforderlichen Wanddicke s0ist der zulässige Spannungsvergleichswert Sm um 20 % zu erniedrigen. Zusätzlich ist nachzuprüfen, dass der Boden im Bereich der Kalotte gegen elastisches Einbeulen ausreichend bemessen ist.
Dies ist der Fall, wenn
| (a 2.5-2) |
ist.
Der Sicherheitsbeiwert fk ist der Tabelle a 2.5-1 zu entnehmen. Wird ein höherer Prüfdruck als p´ = 1,3 ⋅ p gefordert, so ist ein gesonderter Nachweis gegen elastisches Einbeulen zu führen. In diesem Fall darf der Sicherheitsbeiwert f´k beim Prüfdruck den in der Tabelle a 2.5-1 angegebenen Wert nicht unterschreiten.
Tabelle a 2.5-1: Sicherheitsbeiwerte gegen elastisches Einbeulen bei äußerem Überdruck
| s0n / R | fk | f´k |
| 0,001 | 5,5 | 4,0 |
| 0,003 | 4,0 | 2,9 |
| 0,005 | 3,7 | 2,7 |
| 0,010 | 3,5 | 2,6 |
| 0,1 | 3,0 | 2,2 |
| Zwischenwerte sind linear zu interpolieren | ||
Bild a 2.5-3: Berechnungsbeiwerte β für gewölbte Böden in Klöpperform
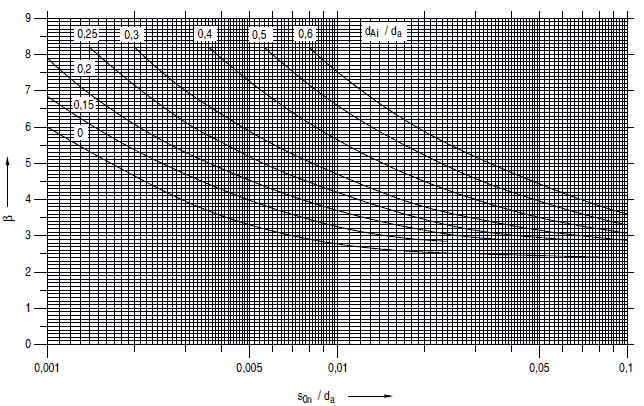
Bild a 2.5-4: Berechnungsbeiwerte β für gewölbte Böden in Korbbogenform
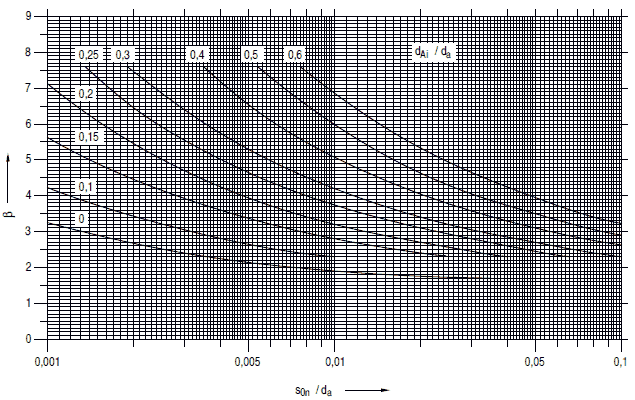
a 2.6 Ebene Platten
a 2.6.1 Berechnungsgrößen und Einheiten zu Abschnitt a 2.6
| Formelzeichen | Berechnungsgröße | Einheit |
| aD | Hebelarm | mm |
| dA | Ausschnittsdurchmesser | mm |
| dD | mittlerer Durchmesser oder Durchmesser des Berührungskreises einer Dichtung | mm |
| di | Innendurchmesser | mm |
| dt | Lochkreisdurchmesser | mm |
| P | Innendruck | MPa |
| R | Übergangsradius | mm |
| s0n, Pl | Nennwanddicke der Platte | mm |
| s0n, Zyl | Nennwanddicke des Zylinders | mm |
| C | Berechnungsbeiwert | - |
| CA | Berechnungsbeiwert bei Ausschnittberechnung | - |
| E | Elastizitätsmodul | N / mm2 |
| FD | Maximale Dichtungskraft unter Berücksichtigung der durch das Anzugsverfahren bedingten Schraubenkraftstreuung | N |
| Sm | Spannungsvergleichswert gemäß Abschnitt 7.7.3.4 | N / mm2 |
a 2.6.2 Geltungsbereich
Die nachstehenden Berechnungsregeln gelten für ebene Platten mit und ohne Randmoment unter Druckbelastung im Bereich
![]()
a 2.6.3 Berechnung
a 2.6.3.1 Mit zylindrischem Schuss fest verbundene runde ebene Platte
(1) Bei der mit einem zylindrischen Schuss verbundenen Platte nach Bild a 2.6-1 sind Platte und Zylinder gemeinsam zu betrachten.
Bild a 2.6-1: Mit einem zylindrischen Schuss fest verbundene ebene Platte
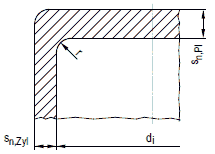
(2) Entsprechend Tabelle 7.7-1, Fußnote1, bestehen zwei Dimensionierungsmöglichkeiten für die Verbindung ebene Platte / Zylinder.
Hinweis:
Alternative 2 erlaubt gegenüber Alternative 1 dünnere ebene Platten bei größeren Zylinderwanddicken.
| (a 2.6-1) |
Vordimensionierung des Zylinders entsprechend Abschnitt a 2.2.
Kontrolle der Spannungen im Zylinder:
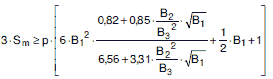
mit |
(a 2.6-2) | ||||||
|
(a 2.6-3) | ||||||
|
(a 2.6-4) | ||||||
|
(a 2.6-5) |
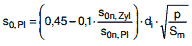 |
(a 2.6-6) |
Vordimensionierung des Zylinders entsprechend Abschnitt a 2.2.
Kontrolle der Spannungen im Zylinder:
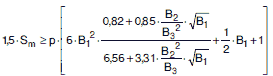 |
(a 2.6-7) |
mit
|
(a 2.6-8) | ||||||
|
(a 2.6-9) | ||||||
|
(a 2.6-10) |
Bei beiden Alternativen kann es erforderlich sein, die bei der Vordimensionierung erhaltenen Wanddicken für Platte oder Zylinder oder in Kombination für Platte und Zylinder zu vergrößern und die Kontrolle der Spannungen im Zylinder am Übergang zur Platte nach Gleichung (a 2.6-2) oder (a 2.6-7) zu wiederholen.
a 2.6.3.2 Unverankerte runde Platten mit zusätzlichem Randmoment
(1) Bei ebenen, am Rande verschraubten und mit einem Dichtelement versehenen Platten ist neben der Festigkeitsberechnung nach Gleichung (a 2.6-11) eine Verformungsbetrachtung nach Gleichung (a 2.6-14) durchzuführen, damit ein Dichtbleiben der Verbindung sichergestellt ist, wobei der Einbauzustand, der Prüfzustand und der Betriebszustand in Betracht zu ziehen sind.
(2) Die erforderliche Wanddicke s0 unverankerter runder Platten mit zusätzlichem gleichsinnigen Randmoment nach Bild a 2.6-2 beträgt
| (a 2.6-11) |
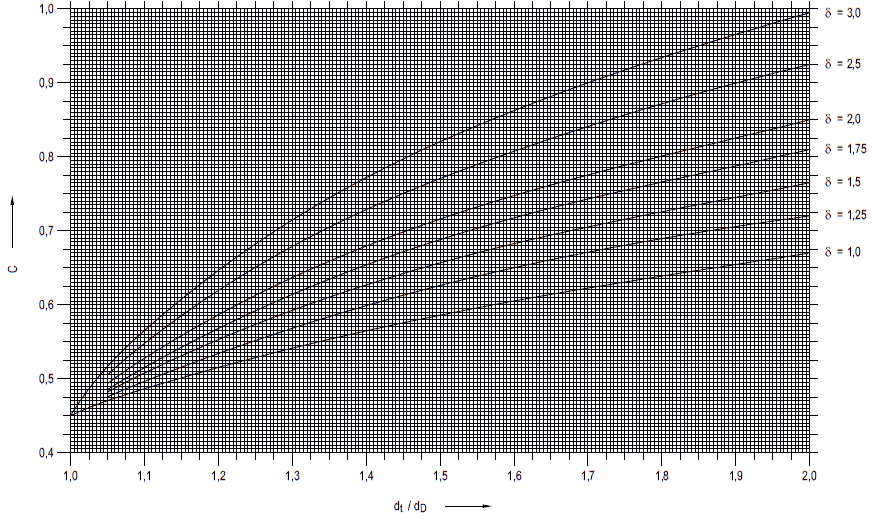
Der C-Wert ist in Abhängigkeit vom Verhältnis dt / dD und dem Wert δ aus Bild a 2.6-3 zu entnehmen. Hierbei beträgt das Verhältnis der erforderlichen Schraubenkraft zur Innendruckkraft
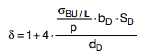 |
(a 2.6-12) |
wobei in der Regel SD = 1,2 eingesetzt wird. Dichtungsbreite bD gemäß Abschnitt a 2.10.
Das gleiche Ergebnis für den C-Wert wie Bild a 2.6-3 liefert die Gleichung:
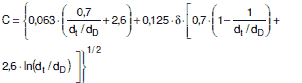 |
(a 2.6-13) |
Die Durchbiegung der Platte mit der Wanddicke s0 nach Gleichung (a 2.6-11) sollte im Hinblick auf Dichtheitsanforderungen mit Hilfe der Gleichung (a 2.6-14) überprüft werden.
Bei Begrenzung der Durchbiegung auf z.B. w = 0,001 - dD ist in Gleichung (a 2.6-14) für x = 0,001 einzusetzen.
| (a 2.6-14) |
mit der Dichtungskraft FD nach Abschnitt a 2.8 und dem Hebelarm
|
(a 2.6-15) |
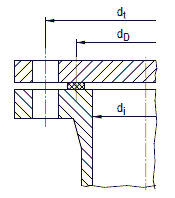
Bild a 2.6-2: Runde ebene Platten mit zusätzlichem Randmoment
a 2.6.3.3 Ausschnitte in runden ebenen Platten
(1) Ausschnitte in ebenen Platten nach Bild a 2.6-1 sind entsprechend Abschnitt a 2.7.2.3.1 zu verstärken.
(2) Die erforderliche Wanddicke s0 der ebenen Platte mit zusätzlichem Randmoment nach Abschnitt a 2.6.3.2 ergibt sich aus der Gleichung (a 2.6-11), indem der C-Wert nach Bild-a 2.6-3 oder nach Gleichung (a 2.6-13) mit dem Berechnungsbeiwert CA multipliziert wird. Der Wert CA ist wie folgt zu bestimmen, wobei dA der Ausschnittsdurchmesser ist:
|
(a 2.6-16) |
|
(a 2.6-17) |
(3) Bei einem Durchmesserverhältnis dA / di > 0,7 ist die Platte als Flansch nach Abschnitt a 2.9 zu berechnen.
(4) Nichtmittige Ausschnitte dürfen wie zentrale Ausschnitte behandelt werden.
Bild a 2.6-3: Berechnungsbeiwert C von ebenen runden Platten mit gleichsinnigem zusätzlichem Randmoment
a 2.7 Ausschnittverstärkungen
a 2.7.1 Berechnungsgrößen und Einheiten zu Abschnitt a 2.7
| Formelzeichen | Berechnungsgröße | Einheit |
| dAa | Außendurchmesser des Abzweigs | mm |
| dA | Ausschnittsdurchmesser | mm |
| dAe | Innendurchmesser des Ausschnitts zuzüglich des doppelten Korrosionszuschlages c2 | mm |
| dAi | Innendurchmesser der Ausschnittsverstärkung zuzüglich des doppelten Korrosionszuschlags c2 | mm |
| dAm | mittlerer Durchmesser des Stutzens | mm |
| dHi | innerer Durchmesser des Grundkörpers | mm |
| dHm | mittlerer Durchmesser des Grundkörpers an der Ausschnittstelle | mm |
| eA | Bereich der Verstärkung, senkrecht zur Wand des Grundkörpers gemessen | mm |
| eH | halbe Breite des Verstärkungsbereichs, längs der Mittelebene des Grundkörpers gemessen | mm |
| e´H | halbe Breite des Bereichs, in dem 2 / 3 der Verstärkung liegen sollen | mm |
| l | (siehe Bild a 2.7-10) | mm |
| r1, r2, r3 | Rundungsradien | mm |
| sA | Nennwanddicke des Stutzens mit Be- rücksichtigung der Verstärkung, jedoch abzüglich der Zuschläge c1 und c2 | mm |
| sA0 | rechnerisch erforderliche Wanddicke des Stutzens | mm |
| sH | Nennwanddicke der Schale, des Be hälters oder des Bodens an der Ausschnittstelle mit Berücksichtigung der Verstärkung, jedoch abzüglich der Zuschläge c1 und c2 | mm |
| sH0 | rechnerisch erforderliche Wanddicke des Grundkörpers | mm |
| sR | Nennwanddicke der angeschlossenen Rohrleitung abzüglich der Zuschläge c1 und c2 | mm |
| x | Breite des Neigungsversatzes | mm |
| Ae | Querschnittsfläche der erforderlichen Verstärkung eines Ausschnitts | mm2 |
| A1, A2, A3 | nutzbare Verstärkungsfläche | mm2 |
| F | Korrekturfaktor gemäß Bild a 2.7-1 | ¯ |
| α | Neigungswinkel (siehe auch die Bilder a 2.7-2, a 2.7-3 und a 2.7-4) | Grad |
| β | Abzweigwinkel | Grad |
| δ5 | Bruchdehnung | % |
a 2.7.2 Allgemeine Dimensionierung
a 2.7.2.1 Geltungsbereich
(1) Der Geltungsbereich nachstehender Berechnungsregeln entspricht den in den Abschnitten a 2.2 bis a 2.6 und a 4.6 aufgeführten Bereichen.
(2) Die Berechnungsregeln berücksichtigen nur durch inneren Überdruck hervorgerufene Beanspruchungen. Zusätzliche Kräfte und Momente müssen gesondert berücksichtigt werden.
(3) Der Abzweigwinkel β muss größer als oder gleich 60° sein.
a 2.7.2.2 Allgemeines
(1) Ausschnitte sollen rund oder elliptisch sein. Weitere Anforderungen ergeben sich bei Anwendung der Spannungsindex-Methoden nach den Abschnitten 8.2.2.1 bis 8.2.2.3. In dem Falle sind die konstruktiven Voraussetzungen für die Spannungsindex-Methode gemäß Abschnitt 8.2.2 einzuhalten.
(2) Die Verstärkung eines Ausschnittes in einem Grundkörper darf wie folgt vorgenommen werden:
Im Hinblick auf eine beanspruchungsgerechte Formgebung ist die Ausführung c) zu bevorzugen.
(3) Bei der Verstärkung eines Ausschnittes sind folgende Durchmesser- und Wanddickenverhältnisse einzuhalten:
Ein Wanddickenverhältnis sA / sH ist bis maximal 2 zulässig für dAi gleich oder kleiner als 50 mm. Dies gilt auch für Stutzen mit dAi größer als 50 mm, sofern das Durchmesserverhältnis dAi / dHi gleich oder kleiner als 0,2 ist.
Bei Stutzen mit einem Durchmesserverhältnis dAi / dHi größer als 0,2 soll grundsätzlich sA / sH den Wert 1,3 nicht überschreiten. Größere Werte sind erlaubt, wenn
Stutzen größer als oder gleich 120 mm Innendurchmesser sind mit mindestens der 2fachen Wanddicke wie die anschließenden Rohrleitungen auszuführen, wobei sich der Faktor auf die rechnerische Rohrwanddicke bezieht. Auf die Istwanddicke bezogen muss der Faktor mindestens 1,5 betragen.
(4) Eine Ausschnittverstärkung ist nicht erforderlich und der Nachweis für Ausschnitte nach a 2.7.2.3 muss nicht geführt werden, falls:
Hinweis:
Definition eines örtlich beanspruchten Bereichs siehe Abschnitt 7.7.2.2.
(5) Werkstoffpaarungen
Bestehen Grundkörper und Stutzen aus Werkstoffen unterschiedlicher zulässiger Spannungen, so ist, wenn der Grundkörperwerkstoff die kleinere zulässige Spannung aufweist, diese für die Berechnung der gesamten Konstruktion maßgebend. Hierbei muss vorausgesetzt werden, dass das Verformungsvermögen des Stutzenwerkstoffs nicht nennenswert kleiner ist als das des Grundkörperwerkstoffs.
Wenn der Stutzenwerkstoff eine geringere zulässige Spannung aufweist, so sind die im Bereich der geringeren zulässigen Spannungen anzuordnenden Verstärkungsflächen im Verhältnis der zulässigen Spannungen zu vergrößern.
Unterschiede bis zu 4 %-Punkten in den Bruchdehnungen der Werkstoffe von Grundkörper und Abzweig werden als nicht nennenswerter Unterschied des Verformungsvermögens der Werkstoffe angesehen, wobei δ5 14 % nicht unterschreiten darf.
Haben Grundkörperwerkstoff und Stutzenwerkstoff unterschiedliche Wärmedehnungszahlen, so darf ihre Differenz 15 % der Wärmedehnungszahl des Grundkörperwerkstoffs nicht überschreiten.
a 2.7.2.3 Berechnung
a 2.7.2.3.1 Erforderliche Verstärkung
(1) Die gesamte Querschnittsfläche a der erforderlichen Verstärkung eines Ausschnittes in Zylinder-, Kugel-, Kegelschalen und gewölbten Böden unter Innendruck muss der folgenden Bedingung genügen:
| a> dAe ⋅ sH0 ⋅ F | (a 2.7-1) |
wobei der Faktor F für rechtwinklige Stutzen gilt und gleich 1 in allen dimensionierungsbestimmenden Ebenen ist. Bei Zylinder- oder Kegelschalen ist F für eine nicht dimensionierungsbestimmende Ebene in Abhängigkeit von deren Winkellage zu der betrachteten Ebene dem Bild a 2.7-1 zu entnehmen.
Bild a 2.7-1: Ermittlung des Korrekturfaktors F für rechtwinklige Stutzen in Zylinder- oder Kegelschalen
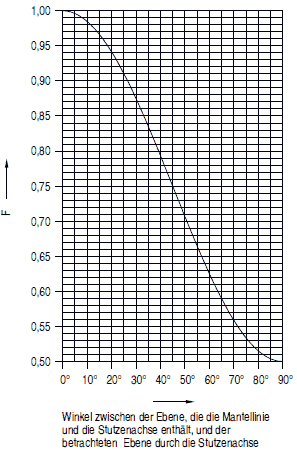
(2) Ausschnitte in ebenen Böden, die den halben Bodendurchmesser nicht überschreiten, müssen mindestens folgende Verstärkungsflächen aufweisen:
| a> 0,5 ⋅ dAe⋅ sH0 | (a 2.7-2) |
a 2.7.2.3.2 Mittragende Längen
(1) Die mittragende Länge des Grundkörpers ist wie folgt zu ermitteln:
| eH = dAe | (a 2.7-3) |
oder
| eH = 0,5 ⋅ dAe + sH+ sA | (a 2.7-4) |
Der größere der beiden Werte ist der Berechnung zugrunde zu legen. Zusätzlich gilt, dass 2/3 der Verstärkungsfläche innerhalb eines Bereiches der Länge 2 ⋅ e´H liegen müssen (Bilder a 2.7-8 bis a 2.7-10), wobei e´H der größere Wert ist von entweder
| e´H = 0,5 ⋅ (dAe + (0,5 ⋅ dHm ⋅ sH)0,5
oder |
(a 2.7-5) |
| e´H = 0,5 ⋅ dAe + 2 / 3 ⋅ (sH + sA) | (a 2.7-6) |
(2) Die mittragende Länge für Stutzen gemäß den Bildern a 2.7-2, a 2.7-3, a 2.7-5, a 2.7-6 ist wie folgt zu ermitteln:
| eA = 0,5 ⋅ ((0,5 ⋅ dAm ⋅ SA+r2)0,5)
worin |
(a 2.7-7) |
| dAm = dAi + sA | (a 2.7-8) |
ist.
Im Falle eines Stutzens mit konischer Innenfläche nach Bild 2.7-6 ist die mittragende Länge unter Verwendung der Werte dAi und sA an der Stelle des äußeren Durchmessers des Grundkörpers zu bestimmen.
(3) Die mittragende Länge für Stutzen gemäß den Bildern a 2.7-4 und a 2.7-7 ist wie folgt zu bestimmen:
| eA = 0,5 ⋅ (0,5 ⋅ dAm ⋅ SA)0,5
wobei |
(a 2.7-9) |
| dAm = dAi + sA | (a 2.7-10) |
und zusätzlich für Ausschnittverstärkungen gemäß Bild a 2.7-4
| sA = sR + 0,667 ⋅ x | (a 2.7-11) |
ist.
Im Fall eines Stutzens mit konischer Innenfläche gemäß Bild a 2.7-7 ist die obere Grenzlinie der Verstärkungsfläche gegebenenfalls iterativ unter Verwendung der Werte dAi und sA im Schwerpunkt dieser Stutzenverstärkungsfläche zu bestimmen.
a 2.7.2.3.3 Beanspruchungsschema für nutzbare Verstärkungsflächen
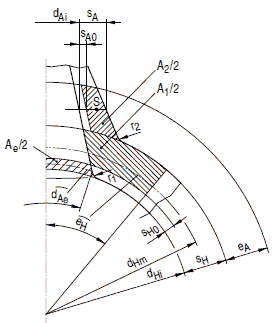
(1) Die für die Erfüllung der Gleichung (a 2.7-1) nutzbaren Verstärkungsflächen A1, A2, A3 sind in den Bildern a 2.7-8 bis a 2.7-11 dargestellt, sie muss die Bedingung A1 + A2 + A3 größer als oder gleich a erfüllen.
(2) Eine gegenseitige Beeinflussung von Stutzenausschnitt und Übergang Kegel - Zylinder ist nur dann zu berücksichtigen, wenn
| l < 2,5 ⋅ ((dHm / 2) ⋅ SH)0,5 | (a 2.7-12) |
ist.
Dabei ist
| dHm = dHi + sH | (a 2.7-13) |
Bilder a 2.7-2 bis a 2.7-4: Zulässige Stutzenformen
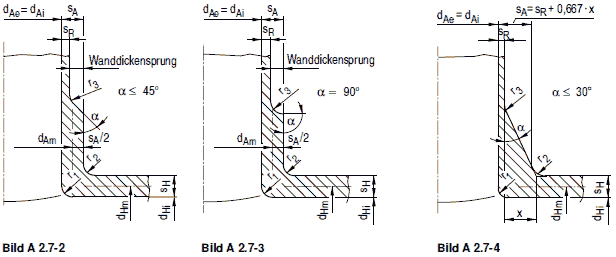
Bilder a 2.7-5 bis a 2.7-7: Zulässige Stutzenformen
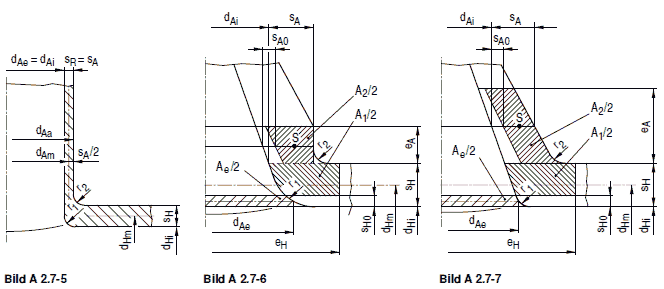
Bild a 2.7-8: Schräger zylindrischer Abzweig
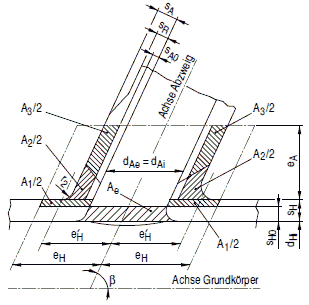
Bild a 2.7-9: Schräger konischer Abzweig
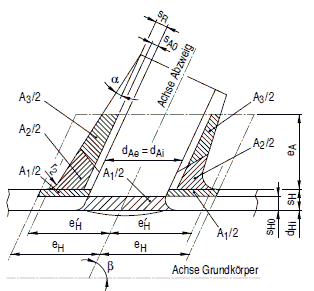
Bild a 2.7-10: Kegelschale mit Ausschnittsverstärkung
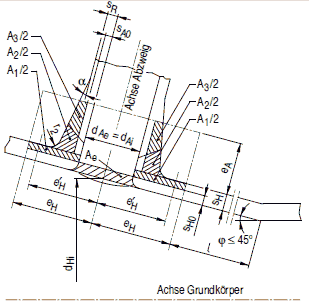
Bild a 2.7-11: Konischer Abzweig in einer Kugelschale
a 2.7.3 Alternative Dimensionierung von Ausschnittsverstärkungen
a 2.7.3.1 Zylinderschalen
Im Falle der Anwendung der alternativen Spannungsindex-Methode gemäß Abschnitt 8.2.2.2 gilt für die Berechnung der Verstärkungsflächen nach Abschnitt a 2.7.2 folgende alternative Vorschrift:
| dAi / (dHi⋅ sH0 / 2)0,5 | Verstärkung |
| < 0,2 | 0 |
| von 0,2 bis 0,4 | |
| > 0,4 | 0,75 ⋅ dAi ⋅ sH0 |
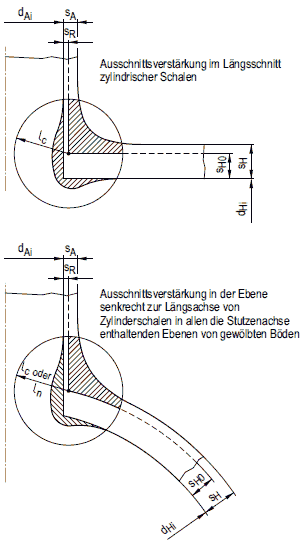
Für die mittragende Zone gilt Bild a 2.7-12.
lc (siehe Bild a 2.7-12) ist nach Gleichung (a 2.7-14) zu ermitteln:
| lc = 0,75 ⋅ (sH0 / dHi) 2/3 ⋅ dHi | (a 2.7-14) |
ln (siehe Bild a 2.7-12) ist nach Gleichung (a 2.7-15) zu ermitteln:
| ln = (sH0 / dAi) 2/3 ⋅ (dAi / dHi + 0,5) ⋅ dHi | (a 2.7-15) |
Die Berechnungseinheiten sind dem Abschnitt a 2.7.1 zu entnehmen.
Bild a 2.7-12: Mittragende Zone
a 2.7.3.2 Gewölbte Böden
Im Falle der Anwendung der alternativen Spannungsindex-Methode gemäß Abschnitt 8.2.2.2 gilt für die Berechnung der Verstärkungsflächen nach Abschnitt a 2.7.2 folgende alternative Vorschrift:
| dAi / (dHi⋅ sH0 / 2)0,5 | Verstärkung |
| < 0,2 | 0 |
| von 0,2 bis 0,4 | |
| > 0,4 | dAi ⋅ sH0 ⋅cosµµ =sin-1 (dAi / (dHi) |
Für die mittragende Zone gilt Bild a 2.7-12.
Die Berechnungseinheiten sind dem Abschnitt a 2.7.1 zu entnehmen.
a 2.8 Schraubenverbindungen
a 2.8.1 Berechnungsgrößen und Einheiten zu Abschnitt a 2.8.
| Formelzeichen | Berechnungsgröße | Einheit |
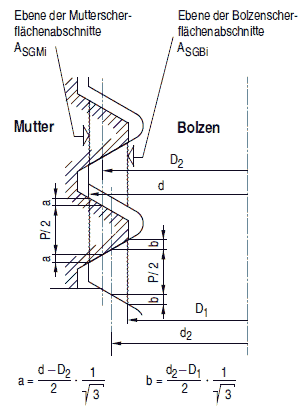
| a, b, c | geometrische Größen bei Bolzen- und Muttergewinde gemäß Bilder a 2.8-3 und a 2.8-4 | mm |
| bD | Dichtungsbreite gemäß Abschnitt a 2.10 | mm |
| c | Konstruktionszuschlag | mm |
| d | Schraubendurchmesser = Gewindeaußendurchmesser | mm |
| d2 | Flankendurchmesser des Schraubengewindes | mm |
| di | Rohr-(Mantelinnendurchmesser | mm |
| diL | Durchmesser einer Innenbohrung einer Schraube | mm |
| dD | mittlerer Dichtungsdurchmesser | mm |
| dD1, dD2 | mittlerer Dichtungsdurchmesser bei Metall-O-Ringdichtungen | mm |
| dk | Gewindekerndurchmesser | mm |
| dM | äußerer Durchmesser der Kontaktstelle der beiden Flansche im Kraftnebenschluss | mm |
| ds | Schaftdurchmesser einer Dehnschraube | mm |
| dt | Lochkreisdurchmesser | mm |
| k*1 , k*11 k*12 | Dichtungskennwerte für Metall-O-Ringdichtungen | N / mm |
| l | effektive Einschraubtiefe oder Mutter- höhe | mm |
| lB | Länge des fertigungsbedingten konisch auslaufenden Muttergewindeendes | mm |
| leff | (Bild a 2.8-5) vergleiche "l" | mm |
| lges | Gesamt-Einschraubtiefe oder -Mutter- höhe | mm |
| n | Anzahl der Schraubenlöcher | ¯ |
| p | Auslegungsdruck | MPa |
| p' | Prüfdruck | MPa |
| A0 | Querschnittsfläche des Dehnschaftes | mm2 |
| AS | Spannungsquerschnitt | mm2 |
| ASG Bolzen | Scherfläche des Bolzengewindes | mm2 |
| ASG Bi | Ebene der Bolzenscherflächenab- schnitte | mm2 |
| ASG Mutter | Scherfläche des Muttergewindes | mm2 |
| ASG Mi | Ebene der Mutterscherflächenab- schnitte | mm2 |
| ASGSackloch | Scherfläche des Sackloches | mm2 |
| C1, C2, C3 | Festigkeitsminderungsfaktoren | ¯ |
| D | Muttergewinde / Sacklochgewinde - Außendurchmesser | mm |
| D1 | Muttergewinde / Sacklochgewinde -Kerndurchmesser | mm |
| D2 | Muttergewinde / Sacklochgewinde -Flankendurchmesser | mm |
| Dc | innerer Durchmesser der Mutterauflagefläche, Durchmesser der Aussenkung | mm |
| Dm | mittlerer Durchmesser des konisch auslaufenden Muttergewindeendes | mm |
| Dmax | maximaler Durchmesser des konisch auslaufenden Muttergewindeendes | mm |
| D1 max | (siehe Bild a 2.8-4) | mm |
| FDBO | zulässige Standkraft der Dichtung im Betriebszustand bei Krafthauptschlussverbindungen | N |
| FDBU / L | erforderliche Dichtungskraft für den Betriebszustand bei Krafthauptschlussverbindungen | N |
| FDKU | erforderliche Dichtungskraft zum Erreichen der Blocklage | N |
| FDVO | zulässige Standkraft der Dichtung im Einbauzustand bei Krafthauptschlussverbindungen | N |
| FDVU / L | Vorverformungskraft | N |
| FF | Ringflächenkraft im Auslegungszustand | N |
| F´F | Ringflächenkraft im Prüfzustand | N |
| Fmax Bolzen | Bruchkraft des freien belasteten Bolzengewindes oder des Dehnschaftes | N |
| Fmax GBolzen | Bruchkraft des im Eingriff befindlichen Bolzengewindes | N |
| Fmax G Mutter | Bruchkraft des im Eingriff befindlichen Muttergewindes | N |
| FR | gesamte Rohrkraft | N |
| FRM | zusätzliche Rohrkraft aus dem Rohrmoment | N |
| FRM0 | zusätzliche Rohrkraft aus dem Rohrmoment im Einbauzustand | N |
| F´RM | Zusätzliche Rohrkraft aus dem Rohrmoment für den Prüfzustand | N |
| FRP | Rohrkraft infolge Innendruck | N |
| FRZ | zusätzliche Rohrlängskraft | N |
| FRZ0 | zusätzliche Rohrlängskraft im Einbau- zustand | N |
| F´RZ | zusätzliche Rohrlängskraft für den Prüfzustand | N |
| FR0 | im Rohrsystem vorhandene Rohrkraft im Einbauzustand | N |
| FS | Schraubenkraft (allgemein) | N |
| FS0U | Schraubenkraft für den Einbauzustand (untere Grenze) | N |
| FSB | Schraubenkraft für den Betriebszu- stand bei Kraftnebenschlussverbindungen | N |
| FSBU | Schraubenkraft für den Betriebszu- stand bei Kraftnebenschlussverbindungen (untere Grenze) | N |
| FSBU / L | Mindestwert der Schraubenkraft für den Betriebszustand bei Krafthauptschlussverbindungen | N |
| FSBx | Schraubenkraft für den Betriebszustand bei Krafthauptschlussverbindungen | N |
| FSKU | Mindestwert der Schraubenkraft zum Erreichen der Blocklage bei Kraftnebenschlussverbindungen | N |
| FS0 | Schraubenkraft für den Einbauzustand | N |
| F´S | Schraubenkraft für den Prüfzustand | N |
| FSPU | Schraubenkraft für den Prüfzustand (untere Grenze) | N |
| FZx | axiale Zusatzkraft zur Übertragung von Querkräften und Torsionsmomenten im Reibschluss beim Betriebszustand | N |
| FZ0 | axiale Zusatzkraft zur Übertragung von Querkräften und Torsionsmomenten im Reibschluss beim Einbauzustand | N |
| F´Z | axiale Zusatzkraft zur Übertragung von Querkräften und Torsionsmomenten im Reibschluss beim Prüfzustand | N |
| MB | Biegemoment im Rohr | N⋅ mm |
| Mt | Torsionsmoment im Rohr | N⋅ mm |
| P | Steigung des Gewindes | mm |
| Q | Querkraft im Rohr | N |
| RmB | Zugfestigkeit des Schraubenbolzenwerkstoffes | N / mm2 |
| RmM | Zugfestigkeit des Mutterwerkstoffes | N / mm2 |
| RmS | Zugfestigkeit des Sacklochwerkstoffes | N / mm2 |
| Rp0,2T | 0,2%-Dehngrenze bei Betriebs- bzw. Prüftemperatur | N / mm2 |
| Rp0,2RT | 0,2%-Dehngrenze bei Raumtemperatur | N / mm2 |
| RS | Festigkeitsverhältnis | ¯ |
| SD | Sicherheitsbeiwert | ¯ |
| SW | Schlüsselweite | mm |
| α | Flankenwinkel | Grad |
| µD | Reibwert der Dichtung | ¯ |
| µM | Reibwert der metallischen Kontaktfläche | ¯ |
| σDB | Vorhandene mittlere Flächenpressung der Dichtung im Betriebszustand | N / mm2 |
| σBO | Oberer Grenzwert σDB | N / mm2 |
| σBU | Unterer Grenzwert σDB | N / mm2 |
| σBU / L | Mindestflächenpressung im Betriebs- zustand für Krafthauptschlussverbindungen | N / mm2 |
| σKNS | Mindestflächenpressung für Kraftnebenschlussverbindungen | N / mm2 |
| σV | Vorhandene mittlere Flächenpressung der Dichtung beim Vorverformen | N / mm2 |
| σVO | Oberer Grenzwert σV | N / mm2 |
| σVU | Unterer Grenzwert σV | N / mm2 |
| σVU / L | Mindestflächenpressung im Einbauzustand für Krafthauptschlussverbindungen | N / mm2 |
| σzul | zulässige Spannung nach Tabelle 7.7-7 | N / mm2 |
a 2.8.2 Geltungsbereich
Die nachstehenden Berechnungsregeln gelten für Schrauben mit kreisförmiger Anordnung in gleichem Abstand als kraftschlüssige Verbindungselemente von druckführenden Teilen. Die in den einzelnen Betriebszuständen erforderlichen Kräfte (Schraubenkraft, Dichtungskraft) werden für Flanschverbindungen mit der Dichtung im Krafthauptschluss (KHS) und Kraftnebenschluss (KNS) bestimmt (siehe Bild a 2.8-1 und Abschnitt a 2.8.4). Voraussetzung für die Anwendung von Flanschverbindungen mit der Dichtung im Kraftnebenschluss ist eine hinreichende Steifigkeit und damit begrenzte Flanschblattneigung. Die Berechnungsregeln berücksichtigen vorwiegend ruhende Zugbeanspruchung. Schub- und Biegebeanspruchungen in den Schrauben, die z.B. aus den Verformungen von Flanschen und Deckeln, aus thermischen Einflüssen (z.B. örtlichen und zeitlichen Temperaturgradienten, unterschiedlichen Wärmedehnzahlen) stammen, sind in diesem Abschnitt nicht erfasst.
Bild a 2.8-1: Darstellung einer Flanschverbindung mit der Dichtung im KHS und im KNS (schematisch)
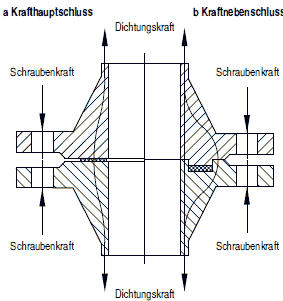
a 2.8.3 Allgemeines
(1) Für verschraubte Flanschverbindungen müssen Dichtheits- und Festigkeitsnachweise durchgeführt werden (siehe Ablaufschema in Bild a 2.8-2). Beim Dichtheitsnachweis ist im Wesentlichen die Höhe der Vorspannung zu bestimmen, die zur Gewährleistung der Dichtheit der Verbindung bei den Betriebs- und Prüffällen erforderlich ist. Beim Festigkeitsnachweis ist die Einhaltung der zulässigen Spannungen für Flansche, Schrauben und Dichtungen nachzuweisen.
(2) Im ersten Schritt sind die Komponenten der Flanschverbindung auszuwählen. Die in den Abschnitten a 2.8.4, a 2.9.4 und a 2.9.5 angegebenen vereinfachten Verfahren sind hierfür geeignet. Dabei werden aus den spezifizierten Belastungen, der gewählten Dichtung (z.B. Abmessungen, Dichtheitsklasse, Dichtungskennwerte) sowie den zulässigen Spannungen der Komponenten der Flanschverbindung die erforderlichen Abmessungen sowie die erforderliche Vorspannkraft der Schrauben bestimmt.
(3) Im zweiten Schritt erfolgen die Dichtheits- und Festigkeitsnachweise und eine Überprüfung der Abtragbarkeit der Schnittlasten (auch Querkraft und Torsionsmoment). Das Schraubenanzugsverfahren (z.B. Anzugsfaktor) ist beim Festigkeitsnachweis der Flansche und Schrauben zu berücksichtigen.
Der Dichtheitsnachweis ist mit der minimalen rechnerischen Schraubenkraft zu führen. Bei Kraftnebenschlussverbindungen mit einer Schraubenanzahl n gleich oder größer als 8 darf abweichend hiervon der Nachweis mit einer mittleren rechnerischen Schraubenkraft geführt werden.
Die Festigkeitsnachweise des Flansches und bei Krafthauptschlussverbindungen der Dichtung sind im Einbauzustand mit der maximalen rechnerischen Schraubenkraft zu führen, bei den Festigkeitsnachweisen im Betriebszustand darf die mittlere rechnerische Schraubenkraft zugrunde gelegt werden.
Für den Festigkeitsnachweis der Schrauben ist die maximale Schraubenkraft anzusetzen.
(4) Können die Dichtheits- und Festigkeitsnachweise nicht erbracht werden, ist eine iterative Vorgehensweise mit einer Wiederholung der Nachweise erforderlich, bis die Bedingungen erfüllt sind.
(5) Als Dehnschrauben werden solche Schrauben bewertet, deren Schaftdurchmesser kleiner als oder gleich dem 0,9fachen des Kerndurchmessers ist und deren Dehnschaftlänge mindestens das Zweifache, möglichst aber das Vierfache des Schaftdurchmessers beträgt, oder solche Schrauben, deren Abmessungen DIN 2510-1 bis DIN 2510-4 entsprechen. Als Dehnschrauben dürfen auch Schaftschrauben mit vergrößerter Dehnlänge und einem Schaftdurchmesser kleiner oder gleich dem Kerndurchmesser verwendet werden, wenn deren Nachgiebigkeit bezüglich der Längung und deren Nachgiebigkeit bezüglich der Biegung unter den gegebenen Randbedingungen der Nachgiebigkeit einer Dehnschraube gemäß vorstehender Definition mit gleichem Gewindekerndurchmesser und minimaler Dehnschaftlänge gemäß oben getroffener Festlegung entspricht.
Bei Schraubenverbindungen nach DIN EN ISO 898-1, DIN EN ISO 898-2, DIN EN ISO 3506-1, DIN EN ISO 3506-2, DIN EN ISO 3506-3, DIN 267-13 und DIN 2510-1 bis DIN 2510-4 darf unter Beachtung der angegebenen Mutterhöhen oder Einschraubtiefen auf eine Nachrechnung der Gewindebeanspruchung verzichtet werden.
Andernfalls ist die Berechnung nach Abschnitt a 2.8.4 oder nach VDI 2230 durchzuführen.
Bild a 2.8-2: Allgemeines Ablaufschema für die Berechnung von Flanschen
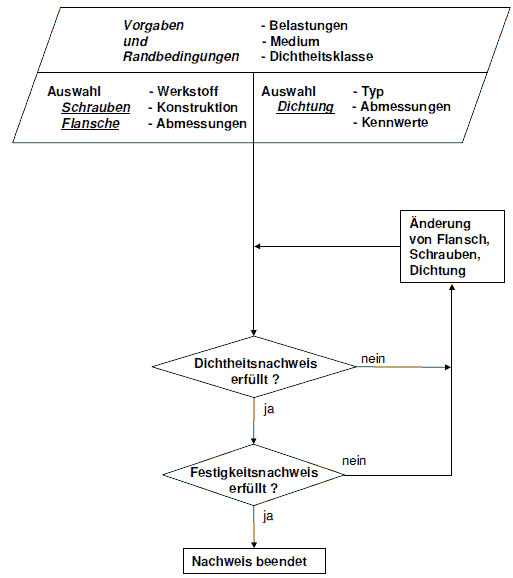
a 2.8.4 Dimensionierung von Schrauben
a 2.8.4.1 Schraubenkraft für Krafthauptschluss
Die Schraubenkraft (FS) ist zu ermitteln für den Betriebszustand (FSBx), für den Prüfzustand (F´S ) und für den Einbauzustand (FS0).
| FSBU / L = FR + FDBU / L + FF + FZ | (a 2.8-1) |
Als Rohrkraft FR ist die vom Rohr oder Mantel auf die Flanschverbindung übertragene Kraft zu verstehen. Die Rohrkraft ergibt sich bei geschlossenen Rohren oder Mänteln nach folgender Gleichung:
| FR = FRP + FRZ + FRM | (a 2.8-2) |
dabei ist
| FRP = di2 ⋅ π ⋅ p / 4 | (a 2.8-3) |
Die zusätzlichen Rohrkräfte FRZ und FRM berücksichtigen Rohrlängskräfte FRZ und Rohrbiegemomente MB, wobei
| FRM = 4 ⋅ MB / dD | (a 2.8-4) |
Auf Grundlage der vorhandenen Steifigkeitsverhältnisse darf anstelle des Dichtungsdurchmessers dD der wirksame Durchmesser verwendet werden.
Beim Spannungsnachweis der Schrauben darf anstelle des Dichtungsdurchmessers dD der Lochkreisdurchmesser dt eingesetzt werden.
FRZ und MB müssen gegebenenfalls der statischen oder dynamischen Rohrleitungssystemanalyse entnommen werden.
FRZ und MB sind gleich 0 bei Flanschverbindungen in Behältern und Rohrleitungen, an die keine oder nur Rohrleitungen ohne zusätzliche Längskraft FRZ und ohne zusätzliches Rohrbiegemoment MB angeschlossen sind.
Die erforderliche Dichtungskraft für den Betriebszustand (FDBU / L) ermittelt sich aus:
| FDBU / L = π⋅ dD ⋅ bD ⋅ σBU / L ⋅ SD | (a 2.8-5) |
Für SD ist mindestens der Wert 1,2 einzusetzen.
Die erforderliche Dichtungskraft im Betriebszustand FDBU / L ist notwendig, um dauerndes Dichthalten (Dichtheitsklasse L) im Betrieb zu gewährleisten. Die Dichtungskennwerte werden in Abschnitt a 2.10 behandelt.
Bei Schweißlippendichtungen ist zur Sicherstellung der Lagestabilität eine axiale Druckkraft auf die Stirnflächen der Flansche vorzuhalten. Für FDBU / L ist hierfür mindestens der Wert 0, 15 (FRP + FF) zu setzen.
Die zulässige (maximal ertragbare) Standkraft der Dichtung im Betriebszustand beträgt
| FDBO = π ⋅ dD ⋅ bD ⋅ σBO | (a 2.8-6) |
Die Ringflächenkraft FFbeträgt
| (a 2.8-7) |
Die Ringflächenkraft FF wird hervorgerufen durch den Innendruck p und lastet auf der Ringfläche, die durch den Dichtungskreis dD und den Innendurchmesser di gebildet wird. Als Dichtungsdurchmesser dD muss der mittlere Durchmesser der Dichtung angesetzt werden. Bei Schweißlippendichtungen ist der mittlere Durchmesser der Schweißnaht einzusetzen. Bei konzentrischen Doppeldichtungen ist der mittlere Durchmesser der äußeren Dichtung zu verwenden.
Um in der Flanschverbindung eine Querkraft Q (senkrecht zur Rohrachse) und ein Torsionsmoment Mt durch Reibschluss übertragen zu können, muss an der Dichtung erforderlichenfalls eine zusätzliche Kraft FZ angreifen.
FZ beträgt:
aa) für seitlich verschiebbare Flansche, bei denen Querkräfte nur durch Reibschluss übertragen werden können
| (a 2.8-8) |
ab) für seitlich nicht verschiebbare Flansche, bei denen Querkräfte durch Formschluss übertragen werden
| (a 2.8-9) |
Falls keine anderslautenden Versuchsergebnisse vorliegen, sind die Reibbeiwerte wie folgt einzusetzen:
μD = 0,05 bei Dichtungen auf PTFE-Basis
μD = 0,1 bei graphitbeschichteten Dichtungen
μD = 0,15 bei metallischen Auflagen mit glatter Oberfläche
μD = 0,25 bei unbeschichteten Dichtungen auf Faserbasis
| (a 2.8-10) |
Die Größen F´RZ und F´RM entsprechen den zusätzlichen Rohrkräften im Prüfzustand. F´Z ist entsprechend den Gleichungen (a 2.8-8) und (a 2.8-9) unter Berücksichtigung des Prüfzustandes zu ermitteln.
Um diese Bedingungen zu erfüllen, ist zu fordern:
| FS0U> FDVU / L + FRZ0 + FRM0 | (a 2.8-11) |
mindestens jedoch für den Prüfzustand
| FS0U> F´S | (a 2.8-12) |
und für den Betriebszustand
| FS0U> FSBU / L | (a 2.8-13) |
Dabei ist FDVU / L die Vorverformungskraft der Dichtung, die erforderlich ist, um ein ausreichendes Anpassen der Dichtung an die Dichtflächen (Dichtheitsklasse L) zu erreichen.
| FDVU / L = π ⋅ dD ⋅ bD ⋅ σVU / L | (a 2.8-14) |
Im Einbauzustand darf die Dichtung höchstens mit
| FDVO = π⋅ dD ⋅ bD ⋅ σVO | (a 2.8-15) |
belastet werden.
a 2.8.4.2 Schraubenkraft für Kraftnebenschluss
Die Schraubenkraft (FS) ist zu ermitteln für das Erreichen der Blocklage (FSKU), für den Prüfzustand (F´S ) und für den Betriebszustand (FSB). Das Erreichen der Blocklage wird über Gleichung (a 2.9-45) indirekt kontrolliert.
| FSKU = FDKU + FR0 | (a 2.8-16) |
Die erforderliche Dichtungskraft für die Blocklage ermittelt sich für Dichtungen außer Metall-O-Ring-Dichtungen aus:
| FDKU = π⋅ dD ⋅ bD ⋅ σKNS | (a 2.8-17) |
für eine einfache Metall-O-Ring-Dichtung aus:
| FDKU = π⋅ dD ⋅ k*1 | (a 2.8-18) |
und für doppelte Metall-O-Ring-Dichtung aus:
| FDKU = π⋅ (dD1 ⋅ k*11 + dD2 ⋅ k*12) | (a 2.8-19) |
Für einfache Metall-O-Ring-Dichtungen ist der Dichtungskennwert k*1 und für doppelte Metall-O-Ring-Dichtungen die Dichtungskennwerte k*11 und k*12 nach den Unterlagen des Herstellers zu verwenden.
Erforderliche Schraubenkraft für das Einhalten der Blocklage im Betriebszustand
| FSBU = FDKU + FR + FF + FZ | (a 2.8-20) |
Als Rohrkraft FR ist die vom Rohr oder Mantel auf die Flanschverbindung übertragene Kraft zu verstehen. Die Rohrkraft ergibt sich bei geschlossenen Rohren oder Mänteln nach folgender Gleichung:
| FR = FRP + FRZ + FRM | (a 2.8-21) |
dabei ist
| FRP = di2 ⋅ π⋅ p / 4 | (a 2.8-22) |
Die zusätzlichen Rohrkräfte FRZ und FRM berücksichtigen Rohrlängskräfte FRZ und Rohrbiegemomente MB, wobei
| (a 2.8-23) |
FZ beträgt:
aa) für seitlich verschiebbare Flansche, bei denen Querkräfte nur durch Reibschluss übertragen werden können
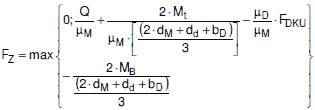 |
(a 2.8-24) |
ab) für seitlich nicht verschiebbare Flansche, bei denen Querkräfte durch Formschluss übertragen werden
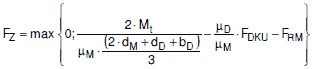 |
(a 2.8-25) |
Falls keine anderslautenden Versuchsergebnisse vorliegen, sind folgende Reibbeiwerte einzusetzen:
μD = 0,10 bei graphitbeschichteten Dichtungen
μM = 0,15 bei metallischen Auflagen mit glatter Oberfläche
| FSPU = p´ / p ⋅ (FRP + FF) + FDKU + F´RZ + F´RM + F´Z | (a 2.8-26) |
Die Größen F´RZ und F´RM entsprechen den zusätzlichen Rohrkräften im Prüfzustand. F´Z ist entsprechend den Gleichungen (a 2.8-24) und (a 2.8-25) unter Berücksichtigung des Prüfzustandes zu ermitteln.
Die Schraubenverbindung ist so anzuziehen, dass beim Einbau die notwendige Schraubenkraft aufgebracht wird, um die Blocklage im Einbauzustand zu erreichen und um die Blocklage weder im Prüfzustand noch im Betriebszustand wieder zu verlassen.
Um diese Bedingungen zu erfüllen, ist zu fordern:
| FS0U> max (FSKU + FZ0; FSBU; FSPU) | (a 2.8-27) |
Hierbei ist FZ0 die zum Abtragen der Querkraft oder eines Torsionsmomentes im Einbauzustand erforderliche zusätzliche Kraft, die nach den Gleichungen (a 2.8-24) oder (a 2.8-25) zu ermitteln ist, wobei die Kräfte und Momente für den Einbauzustand einzusetzen sind.
a 2.8.4.3 Vorspannen von Schraubenverbindungen
(1) Die Einbauschraubenkraft ist in kontrollierter Weise aufzubringen. Je nach Schraubenanzugsverfahren erstreckt sich diese Kontrolle z.B. auf das Drehmoment, die Längung der Schrauben, die Dehnung der Schrauben oder die Temperaturdifferenz zwischen Schraube und Flansch. Hierbei sind - abhängig vom Anzugsverfahren - z.B. folgende Einflussgrößen zu beachten: Reibbeiwert, Oberflächengüte, Schmierungszustand, Setzerscheinungen.
(2) Erfolgt das Anziehen der Schrauben mittels Drehmomentenschlüssel, so ist das Anzugsmoment nach einem geeigneten, rechnerischen oder experimentellen Verfahren zu bestimmen, z.B. nach VDI-Richtlinie 2230 Blatt 1.
a 2.8.4.4 Schraubendurchmesser
(1) Der erforderliche Gewindekerndurchmesser dk einer Starrschraube oder der Schaftdurchmesser ds einer Dehnschraube (mit oder ohne Innenbohrung) in einer Schraubenverbindung mit n Schrauben ist nach folgender Gleichung zu berechnen:
| (a 2.8-28) |
mit σzul gemäß Tabelle 7.7-7.
(2) Hierbei sind folgende Lastfälle zu berücksichtigen:
(3) Als Konstruktionszuschlag c ist einzusetzen bei Dehnschrauben c = 0 mm, bei Starrschrauben gilt für die Belastungen der Beanspruchungsstufe 0 in den Zeilen 1 und 2 der Tabelle 7.7-7:
| (a 2.8-29) |
oder
| (a 2.8-30) |
Im Zwischenbereich ist linear zu interpolieren gemäß
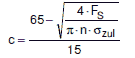 |
(a 2.8-31) |
Für die Lastfälle der übrigen Beanspruchungsstufen ist c = 0 mm zu setzen.
a 2.8.4.5 Erforderliche Einschraubtiefe
a 2.8.4.5.1 Allgemeines
(1) Bei der Ermittlung der erforderlichen Einschraubtiefe in einer zylindrischen Mutter oder im Sackloch soll davon ausgegangen werden, dass die auf der Abstreiffestigkeit beruhende Tragfähigkeit sowohl des Bolzengewindes als auch des Muttergewindes größer ist als die auf der Zugfestigkeit beruhende Tragfähigkeit des freien belasteten Gewindeteils oder des Schaftes bei Dehnschrauben. Die Tragfähigkeit der einzelnen Bereiche berechnet sich wie folgt:
frei belastetes Gewinde:
| Fmax Bolzen = Rm Bolzen ⋅ AS | (a 2.8-32) |
Dehnschaft:
| Fmax Bolzen = Rm Bolzen ⋅ A0 | (a 2.8-33) |
eingeschraubtes Bolzengewinde:
| Fmax G Bolzen = Rm Bolzen ⋅ ASG Bolzen ⋅ C1 ⋅ C2 ⋅ 0,6 | (a 2.8-34) |
eingeschraubtes Muttergewinde:
| Fmax G Mutter = Rm Mutter ⋅ ASG Mutter ⋅ C1 ⋅ C3 ⋅ 0,6 | (a 2.8-35) |
(2) Die Berechnung der Einschraubtiefe ist für den Fall kleinster Flankenüberdeckung gemäß den nachfolgenden Abschnitten vorzunehmen. Hierzu sind bei der Berechnung der tragenden Querschnitte die Bolzenkleinstmaße und die Mutterngrößtmaße einzusetzen.
(3) Bei gegebener Einschraubtiefe oder Mutterhöhe ist nachzuweisen, dass die Tragfähigkeit des freien belasteten Gewindeteils oder des Dehnschaftes kleiner ist als die der ineinandergreifenden Bolzen- und Muttergewindegänge. Bei verringerter Ausnutzung der Schraubenfestigkeit darf die Schraubenkraft FS entsprechend den Abschnitten a 2.8.4.1 oder a 2.8.4.2 zugrunde gelegt werden. Der Nachweis der erforderlichen Einschraubtiefe ist dann gemäß Abschnitt a 2.8.4.5.5 zu erbringen.
(4) Von der Berechnung der Einschraubtiefe gemäß den nachfolgenden Abschnitten ausgenommen sind genormte Schraubenverbindungen. Die Berechnung der Einschraubtiefe gemäß den nachfolgenden Abschnitten einschließlich des Abschnitts a 2.8.4.5.5 gilt nicht für Schraubenverbindungen mit Sägezahn- und Trapezgewinde.
(5) Ergeben sich aus repräsentativen Versuchen kleinere erforderliche Einschraubtiefen als die gemäß den nachfolgenden Abschnitten berechneten, so dürfen diese angewendet werden.
a 2.8.4.5.2 Schraubenverbindungen mit Sackloch oder zylindrischer Mutter ohne Aussenkung
Die erforderliche Einschraubtiefe lges für Schraubenverbindungen mit Sackloch oder zylindrischer Mutter ist als Maximum aus den nachstehend aufgeführten Gleichungen zu ermitteln:
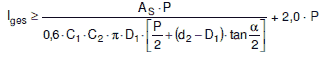 |
(a 2.8-36) |
Bei Dehnschrauben darf anstelle des Spannungsquerschnittes AS der Dehnschaftquerschnitt A0 eingesetzt werden.
Für Spitzgewinde mit Flankenwinkel ± = 60° beträgt
| α | 1 | ||
| tan = | = | ||
| 2 | (3)0,5 |
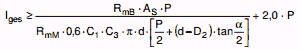 |
(a 2.8-37) |
Im Falle eines Sacklochs ist anstelle RmM die Zugfestigkeit RmS einzusetzen.
| lges> 0,8 ⋅ d | (a 2.8-38) |
Die Größen C1, C2 und C3 sind gemäß Abschnitt a 2.8.4.5.4 zu bestimmen.
Bild a 2.8-3: Darstellung der Größen bei Bolzen- und Muttergewinde
a 2.8.4.5.3 Schraubenverbindungen mit konischem Gewindebereich der Mutter ohne Aussenkung
Die erforderliche Einschraubtiefe lges für Schraubenverbindung mit konischem Gewindebereich der Mutter ist als Maximum aus den nachstehend aufgeführten Gleichungen zu ermitteln.
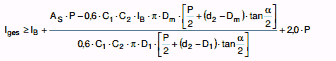 |
(a 2.8-39) |
Die Größen C1, C2, C3 sind gemäß Abschnitt a 2.8.4.5.4 zu bestimmen.
Bild a 2.8-4: Darstellung der Größen bei Bolzen- und Muttergewinde (konisches Muttergewinde)

Bild a 2.8-5: Darstellung der Größen bei der Mutter (mit konischem Teil)
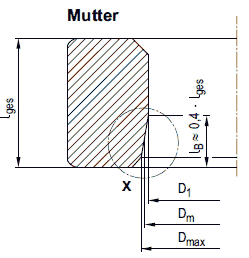
a 2.8.4.5.4 Berechnungsbeiwerte C1, C2, C3
(1) Der Berechnungsbeiwert C1ist gemäß der nachfolgenden Gleichung
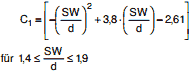 |
(a 2.8-40) |
oder nach Bild a 2.8-6 zu bestimmen.
Im Falle verzahnter Muttern ist anstelle der Schlüsselweite SW ein äquivalenter Wert einzusetzen.
Bild a 2.8-6: Faktor C1 zur Kennzeichnung der Verminderung der Abstreiffestigkeit von Bolzen- und Muttergewinde infolge Mutteraufweitung
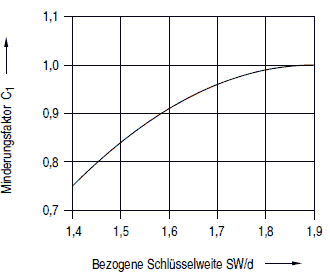
(2) Der Berechnungsbeiwert C2 lässt sich gemäß der Gleichung (a 2.8-46) oder nach Bild a 2.8-7 bestimmen.
Die hierzu erforderlichen Größen berechnen sich wie folgt: Festigkeitsverhältnis RS
| (a 2.8-41) |
Hinweis:
Bei der Ermittlung des Festigkeitsverhältnisses ist der Quotient der Scherflächen ASG Mutter / Sackloch und ASG Bolzen zu bilden, so dass sich die Einschraubtiefe l herauskürzt
Die Scherfläche ASG des Mutter- oder Sacklochgewindes ist
| (a 2.8-42) |
Die Größe der Scherfläche ASGBolzendes Bolzens ist davon abhängig, ob es sich um eine Schraubverbindung mit Sackloch oder Mutter mit zylindrischem Gewinde oder um eine Schraubverbindung mit einer Mutter handelt, die einen konischen Gewindeteil besitzt.
Demnach lautet die Gleichung der Scherfläche ASG Bolzenbei Schraubverbindungen mit Sackloch oder
| (a 2.8-43) |
Die Größe der Scherfläche ASG Bolzeneines Bolzens bei Schraubverbindungen mit Mutter mit konischem Gewindeteil nach Bild a 2.8-5 und unter Berücksichtigung der Beziehung lB = 0,4 ⋅ l lautet:
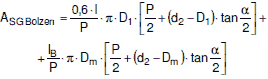 |
(a 2.8-44) |
| Dm errechnet sich aus Dm = 1,015 ⋅ D1 | (a 2.8-45) |
C2 errechnet sich für 1 < RS< 2,2 aus der Gleichung
| C2 = 5,594 - 13,682 ⋅ RS + 14,107 ⋅ RS2 - 6,057 ⋅ RS3 + 0,9353 ⋅ RS4 | (a 2.8-46) |
und für RS< 1 zu C2 = 0,897
C2 kann auch aus Bild a 2.8-7 bestimmt werden.
(3) Der Berechnungsbeiwert C3 berechnet sich für 0,4 d RS < 1 aus der Gleichung
| C3 = 0,728 + 1,769 RS - 2,896 RS2 + 1,296 RS3 | (a 2.8-47) |
und für RS> 1 zu C3 = 0,897
C3 kann auch aus Bild a 2.8-7 bestimmt werden.
Bild a 2.8-7: Faktor zur Kennzeichnung der Verminderung der Abstreiffestigkeit von Bolzen- und Muttergewinde als Folge plastischer Gewindeverformung
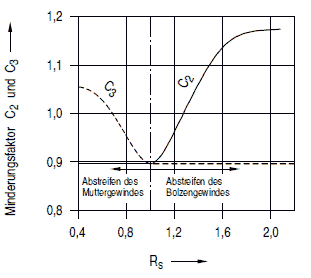
Bild a 2.8-8: Gewindeabmessungen
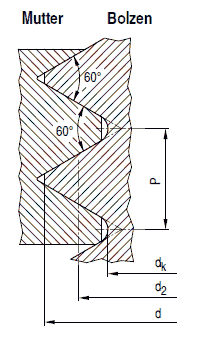
a 2.8.4.5.5 Erforderliche Einschraubtiefe für Armaturengehäuse
(1) Alternativ zum Verfahren nach Abschnitt a 2.8.4.5.1 bis a 2.8.4.5.4 darf bei Armaturen die Einschraubtiefe wie folgt überprüft werden. Der Nachweis gilt als erbracht, wenn folgende Bedingungen erfüllt sind:
| a) l> 0,8 ⋅ d
und |
(a 2.8-48) |
| b) l> 2 ⋅ Fmax / n ⋅ π⋅ d2 ⋅ Sm | (a 2.8-49) |
mit
l: Einschraublänge
n : Anzahl der Schrauben
d, d2: gemäß Bild a 2.8-8
Sm: der kleinere Spannungsvergleichswert der zu verschraubenden Werkstoffe gemäß Abschnitt 7.7.3.4
Fmax: FS oder FS0 (ungünstigster Belastungszustand entsprechend Tabelle 7.7-7)
(2) Der Einbauzustand und die Betriebszustände sind getrennt nachzuweisen.
a 2.9 Flansche
a 2.9.1 Berechnungsgrößen und Einheiten zu Abschnitt a 2.9
| Formelzeichen | Berechnungsgröße | Einheit |
| a | Hebelarm allgemein | mm |
| a1 | Abstand von der Mitte der Schraube zur Schnittstelle C-C | mm |
| aD | Abstand von der Mitte der Schraube zum Angriffspunkt der Dichtungskraft FD | mm |
| aF | Abstand von der Mitte der Schraube zum Angriffspunkt der Ringflächenkraft FF | mm |
| aM | Abstand von der Mitte der Schraube zur äußeren Kontaktstelle der beiden Flansche | mm |
| aR | Abstand von der Mitte der Schraube zum Angriffspunkt der Rohrkraft FR | mm |
| aReib | aReib = 0,5 ⋅ [dt - 0,5⋅ (dFa + dD + bD)] | mm |
| b | Breite des Flanschringquerschnitts | mm |
| bD | Dichtungsbreite gemäß Abschnitt a 2.10 | mm |
| cB | Federsteifigkeit eines Blinddeckels | N / mm |
| cD | Federsteifigkeit der Dichtung | N / mm |
| cD,KNS | Federsteifigkeit der Dichtung im Kraftnebenschluss (bei Rückverformung) | N / mm |
| cS | Federsteifigkeit der Schrauben | N / mm |
| d1 | Los-Flanschring-Innendurchmesser | mm |
| d2 | Los-Flanschring-Außendurchmesser | mm |
| dD | mittlerer Durchmesser oder Durchmesser des Berührungskreises einer Dichtung | mm |
| dD1, dD2 | mittlerer Durchmesser bei doppelter 0- Ring-Dichtung | mm |
| dF | Flansch- oder Bund-Außendurchmesser | mm |
| dFA | äußerer Flanschauflagedurchmesser | mm |
| dKontakt | Durchmesser der Krafteinleitung (FKontakt) bei Kraftnebenschlussverbindungen | mm |
| dM | Äußerer Durchmesser der Kontaktstelle der beiden Flansche im Kraftnebenschluss | mm |
| dL | Schraubenlochdurchmesser | mm |
| d´L | Berechnungsdurchmesser eines Schraubenlochs | mm |
| di | Innendurchmesser von Rohr-, Mantel- oder Flanschring | mm |
| dt | Lochkreisdurchmesser | mm |
| d*t | Fiktiver Auflagedurchmesser von Losflanschen auf Losbunden (siehe Bilder a 2.9-3, a 2.9-5, a 2.9-6) | mm |
| e1, e2 | Schwerpunktabstand | mm |
| f | Höhe einer Dichtleiste | mm |
| gKNS | Relaxationsfaktor | ¯ |
| h | Höhe des Flanschblatts | mm |
| hA | Höhe des kegeligen Ansatzes | mm |
| hB | wirksamer Anteil der Flanschzarge an der Steifigkeit des Flanschanschlusses | mm |
| hD | Höhe der Dichtung | mm |
| hF | wirksame Höhe des Flanschblatts | mm |
| hL | Höhe eines losen Flanschrings | mm |
| hS | Flanschblattdicke zur Aufnahme der Schubspannung im Schnitt C-C | mm |
| N | Anzahl der Schraubenlöcher | - |
| P | Auslegungsdruck | MPa |
| p' | Prüfdruck | MPa |
| pKNS / L | abdichtbarer Druck bei Kraftneben- schlussverbindungen | MPa |
| r, r1 | Übergangsradius siehe Abschnitt 5.2.4.1 (3) | mm |
| s1 | erforderliche Rohr- oder Mantelwand- dicke zur Aufnahme der Längskraft | mm |
| sF | Dicke des Flanschansatzes am Übergang zum Flanschblatt | mm |
| sR | Rohr- oder Mantelwanddicke | mm |
| sx | zum Schnitt X-X gehörige Wandstärke | mm |
| t | Schraubenteilung | mm |
| xS | Schraubenlängung | mm |
| A | Querschnittsfläche | mm2 |
| A1, A2 | Teilquerschnittsflächen gemäß Bild a 2.9-1 | mm2 |
| CF | Drehfedersteifigkeit des Flansches | N ⋅ mm / rad |
| EB, ED, EF, ES | Elastizitätsmodul des Blinddeckel-, Dichtungs-, Flansch- und Schraubenwerkstoffs | N / mm2 |
| EFT | Elastizitätsmodul des Flanschwerkstoffs bei Temperatur | N / mm2 |
| FBZ | Zusatzkraft am Blinddeckel | N |
| FD | Dichtungskraft | N |
| FDB | Betriebsdichtungskraft | N |
| FF | Ringflächenkraft infolge Innendruck | N |
| Fi | Innendruckkraft | N |
| FKontakt | Kraft an der metallischen Auflage bei Kraftnebenschlussverbindungen | N |
| FR | Rohrkraft | N |
| FRP | Rohrkraft infolge Innendruck | N |
| FS | Schraubenkraft | N |
| FS0 | Schraubenkraft im Einbauzustand | N |
| FS0 max | aufgrund des Anziehverfahrens maximal mögliche Schraubenkraft im Einbauzustand, Bestimmung z.B. nach VDI 2230 Blatt 1 | N |
| FS0U | Schraubenkraft für den Einbauzustand (untere Grenze) | N |
| FSB | der jeweiligen Beanspruchungsstufe zugeordnete Schraubenkraft im Betriebszustand | N |
| K, L | Berechnungsbeiwerte | - |
| M | äußeres Stülpmoment beim betrachteten Lastfall | Nmm |
| ME | äußeres Stülpmoment bei Kraftnebenschlussverbindungen im Einbauzustand | Nmm |
| SP1, SP2 | Schwerpunkte der Teilfläche A1 = A2 | - |
| W | Flanschwiderstand | mm3 |
| WA | Flanschwiderstand für den Quer- schnitt A-A | mm3 |
| WB | Flanschwiderstand für den Querschnitt B-B | mm3 |
| Werf | erforderlicher Flanschwiderstand | mm3 |
| Wvorh | vorhandener Flanschwiderstand | mm3 |
| WX | Flanschwiderstand für den Querschnitt X-X | mm3 |
| α | Wärmeausdehnungskoeffizient | 1 / K |
| γzul | zulässiger Neigungswinkel des Flanschblatts gegen die Ebene senkrecht zur Flanschachse | Grad |
| λ | spezifische Leckagerate | mg / (s.m) |
| σVx | Flächenpressung | N / mm2 |
| σzul | zulässige Spannung gemäß Tab. a 2.9-1 | N / mm2 |
| Δh | für die jeweilige Druckstufe und Dicht- heitsklasse zulässige Rückfederung aus der Blocklage gemäß Formblatt a 2.10-2 | mm |
| Δs1, 2 | anteilige Spaltvergrößerung (Flansch 1 und Flansch 2) aufgrund der Flanschblattneigung bei Kraftnebenschlussverbindungen | mm |
Mit dem Index "0" wird der Einbauzustand, mit dem Index "x" der jeweils betrachtete Zustand (Betriebszustand, Prüfzustand) bezeichnet.
a 2.9.2 Allgemeines
(1) Die nachstehende Berechnung gilt für die Dimensionierung und die Festigkeitsnachweise kreisförmiger Flansche aus Stahl, die als kraftschlüssige Verbindungselemente mit Dichtungen im Krafthauptschluss (KHS) und mit Dichtungen im Kraftnebenschluss (KNS) innendruckbeansprucht sind. Voraussetzung für Flanschverbindungen mit der Dichtung im Kraftnebenschluss ist eine hinreichende Steifigkeit und damit eine begrenzte Spalthöhe im Bereich der Dichtung. Unter Flanschen werden im Folgenden Vorschweißflansche, Vorschweißbunde, Losflansche und Deckelflansche verstanden.
(2) Der Dichtheitsnachweis ist mit der minimalen rechnerischen Schraubenkraft zu führen. Bei Kraftnebenschlussverbindungen mit einer Schraubenanzahl n gleich oder größer als 8 darf abweichend hiervon der Nachweis mit einer mittleren rechnerischen Schraubenkraft geführt werden. Bei Kraftnebenschlussverbindungen mit einer Schraubenanzahl n kleiner als 8 ist die Spaltvergrößerung an der Dichtung mit der maximalen Schraubenkraft zu überprüfen.
Die Festigkeitsnachweise des Flansches und der Dichtung im Einbauzustand sind mit der maximalen rechnerischen Schraubenkraft zu führen, bei den Festigkeitsnachweisen im Betriebszustand darf die mittlere rechnerische Schraubenkraft zugrunde gelegt werden.
(3) Ist für Flanschverbindungen der Nachweis einer ausreichenden Dichtheit in den Beanspruchungsstufen C und D erforderlich, so darf dieser durch eine Nachprüfung der Kraft- und Verformungsverhältnisse nach Abschnitt a 2.9.6 oder a 2.9.7 erfolgen.
a 2.9.3 Ausführung und Schweißung
(1) Behälterflansche dürfen geschmiedet oder nahtlos gewalzt werden.
(2) Schweißen und gegebenenfalls notwendige Wärmebehandlungen richten sich nach den komponentenbezogenen Vorschriften.
a 2.9.4 Dimensionierung der Flansche bei Krafthauptschlussverbindungen
a 2.9.4.1 Allgemeines
(1) Die Berechnung besteht aus der Dimensionierung und dem Dichtheits- / Festigkeitsnachweis gemäß Abschnitt a 2.9.6. Die Flanschverbindung muss so bemessen sein, dass sie die Kräfte beim Zusammenbau (Vorverformen der Dichtung), bei der Druckprüfung, im Betrieb bei den An- und Abfahrvorgängen sowie bei eventuellen Störfällen aufnehmen kann.
| σzul, Prüfzustand | |
| Ist der Prüfdruck p´> p ⋅ | |
| σzul, Betriebszustand |
so ist die Berechnung auch für diesen Belastungsfall durchzuführen. Die Bedingung ist sowohl für den Flansch- als auch für den Schraubenwerkstoff zu überprüfen.
(2) Die Flansche sind nach den in den folgenden Abschnitten angeführten Gleichungen zu berechnen. Der Einfluss äußerer Kräfte und Momente ist zu berücksichtigen und nachzuweisen.
(3) Die dem rechnerischen Nachweis zugrunde gelegte Höhe hF oder hL des Flanschblatts muss am ausgeführten Bauteil vorhanden sein. Nuten für normale Feder-, Nut- oder Ring-Joint-Verbindungen brauchen nicht berücksichtigt zu werden.
(4) Maßgebend für die Auslegung der Flansche ist der erforderliche Flanschwiderstand Werf.
(5) Für die Ermittlung des erforderlichen Flanschwiderstands im Betriebszustand für Flansche der Abschnitte a 2.9.4.2 und a 2.9.4.3 in den Schnitten A-a und B-B und für Flansche nach Abschnitt a 2.9.4.4 im Schnitt A-a gilt
|
(a 2.9-1) |
Für die genannten Flansche im Schnitt C-C gilt
|
(a 2.9-2) |
Für die Flansche des Abschnitts a 2.9.4.5 gilt
|
(a 2.9-3) |
Im Einbauzustand gilt für die Flansche der Abschnitte a 2.9.4.2 bis a 2.9.4.5 ohne Rücksicht auf die Schnitte
|
(a 2.9-4) |
mit σzul: zulässige Spannung nach Tabelle a 2.9-1.
Hinweis:
Die Berücksichtigung der maximalen Einbauschraubenkraft FS0max erfolgt im Rahmen des Festigkeitsnachweises, siehe Tabelle a 2.9-1 lfd. Nr. 3.
Bild a 2.9-1: Flanschquerschnitt
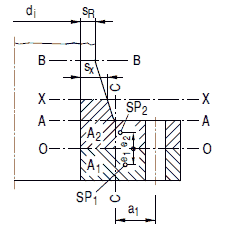
Tabelle a 2.9-1: Zulässige Spannungen σzul für drucktragende Flanschverbindungen aus Stahl oder Stahlguss
| Lfd. Nr. | Spannungsart1 | Einbauzustand | Beanspruchungsstufen | |||
| 0 | A, B | P | C, D | |||
| 1 | Spannung aus Innendruck, erforderlicher Dichtungskraft und äußeren Lasten2
FS = FRP + FF + FDB + FRZ + FRM |
- | Sm | Sm | - | 1 / 1,1 ⋅ Rp0,2RT7, 8 |
| 2 | Spannung im Prüfzustand2
FSP = F´RP + F´RZ + F´RM + F´F + F´DB |
- | - | - | 1 / 1,1 ⋅ Rp0,2RT7 | - |
| 3 | Spannung im Einbauzustand 3, 4
FS0 |
1 / 1,1 ⋅ Rp0,2RT7 | - | - | - | - |
| 4 | Spannung aus Innendruck, äußeren Lasten, Restdichtungskraft und ggf. unterschiedlicher Wärmedehnung5 unter Berücksichtigung des Verspannungszustandes4, 6 |
- | - | 1 / 1,1 ⋅ Rp0,2RT7 | - | - |
Bei Durchmesserverhältnissen dF / di > 2 sind alle Spannungsgrenzen um den Faktor Φ = 0,6 +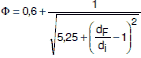 abzumindern. abzumindern.
1) Bedeutung der verwendeten Formelzeichen siehe Abschnitt a 2.9.1. 2) Bei Anwendung der Gleichungen (a 2.9-1) bis (a 2.9-3). 3) Bei Anwendung der Gleichung (a 2.9-4) im Rahmen der Dimensionierung ist FS0U, im Rahmen des Festigkeitsnachweises ist FS0max zu verwenden. 4) Unter Berücksichtigung der Festlegungen in Abschnitt a 2.8.3 (3). 5) Berücksichtigung unterschiedlicher Wärmedehnung bei einer Auslegungstemperatur > 120 °C. Die Temperaturbegrenzung gilt nicht für die Werkstoffpaarung Austenit / Ferrit in Flansch und Schrauben. 6) Bei Berechnung nach Abschnitt a 2.9.6. 7) Bei Stahlguss 0,75 ⋅ Rp0,2T anstelle Rp0,2T / 1,1. 8) Sind für die Beanspruchungsstufen C, D Dichtheitsnachweise zu führen, so ist wie für die Stufen A, B gemäß lfd. Nr. 4 vorzugehen |
||||||
Die Gleichungen (a 2.9-1) bis (a 2.9-3) dürfen sinngemäß auf die Prüffälle angewendet werden.
Die Kräfte F sind nach Abschnitt a 2.8 zu ermitteln.
Die Hebelarme für Dichtungen im Krafthauptschluss betragen:
|
(a 2.9-5) |
|
(a 2.9-6) |
|
(a 2.9-7) |
Bei Vorschweißbunden ist anstelle dt der Teilkreisdurchmesser d*t einzusetzen (siehe Bilder a 2.9-3 und a 2.9-5).
Für Losflansche gilt:
|
(a 2.9-8) |
Für die Berechnung des Flansches stellt die Verwendung von
| d1 + 2 ⋅ r + dF | |
| d*t = | |
| 2 |
und für die Berechnung des Bundes die Verwendung von d*t = dF einen konservativen Ansatz dar.
d*t darf in Abhängigkeit von den Steifigkeitsverhältnissen des Bundes und des Flansches den realen Gegebenheiten angepasst werden.
(6) Der Flanschwiderstand muss allgemein für einen beliebigen Schnitt X-X (Bild a 2.9-1) der Bedingung
| (a 2.9-9) |
genügen.
Dabei ist s1 die infolge der Längskräfte im Flanschansatz erforderliche Wanddicke.
Sie errechnet sich aus folgender Gleichung:
|
(a 2.9-10) |
σzul ist nach Tabelle a 2.9-1 zu bestimmen. Der Faktor Φdarf fÌr Gleichung a 2.9-10 entfallen.
Mit e1 und e2 werden die Schwerpunktabstände der Teilquerschnittsflächen A1 = A2 (im Bild a 2.9-1 durch verschiedene Schraffuren gekennzeichnet) von der für die im angenommenen vollplastischen Zustand geltenden neutralen Linie 0-0 bezeichnet. Der Schwächung des Flanschblatts durch die Schraubenlöcher muss durch den Berechnungsdurchmesser d´L in der nachfolgenden Gleichung Rechnung getragen werden:
Für Flansche mit di> 500 mm ist
| d´L = dL / 2 | (a 2.9-11) |
und für Flansche mit di< 500 mm ist
| d´L = dL ⋅ (1 - di / 1000) | (a 2.9-12) |
a 2.9.4.2 Vorschweißflansche mit innenliegender Dichtung und konischem Ansatz nach Bild a 2.9-2
Der Flansch ist in den Querschnitten A-A, B-B und C-C zu überprüfen, wobei der kleinste Flanschwiderstand für das Festigkeitsverhalten maßgebend ist.
Der vorhandene Flanschwiderstand im Querschnitt bei A-a ergibt sich aus:
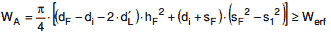 |
(a 2.9-13) |
Die Gleichung (a 2.9-13) darf auch zur Bestimmung von hF verwendet werden.
Bild a 2.9-2: Vorschweißflansch mit konischem Ansatz
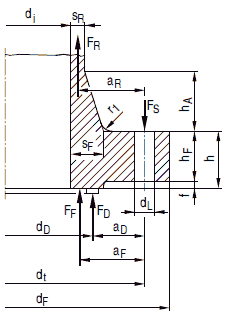
Der vorhandene Flanschwiderstand im Schnitt B-B ergibt sich aus:
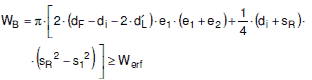 |
(a 2.9-14) |
Die Schwerpunktabstände e1 und e2 bei Flanschen mit konischem Ansatz betragen:
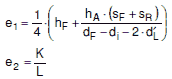 |
(a 2.9-15) |
| e2 = K / L | (a 2.9-16) |
dabei ist
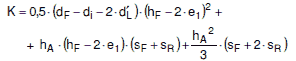 |
(a 2.9-17) |
| L = (dF - di - 2 ⋅ d2L) ⋅ (hF - 2 ⋅ e1) + hA ⋅ (sF + sR) | (a 2.9-18) |
Die zur Aufnahme der Schubbeanspruchung erforderliche Blattdicke hS ergibt sich wie folgt:
im Einbauzustand
|
(a 2.9-19) |
im Betriebszustand
|
(a 2.9-20) |
mit σzul: zulässige Spannung nach Tabelle 2.9-1.
Der Flanschwiderstand im Querschnitt C-C ergibt sich dann aus:
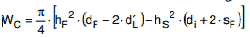 |
(a 2.9-21) |
Das äußere Moment beträgt in diesem Fall
| MC = FS ⋅ a1 | (a 2.9-22) |
mit
FS = FS0U im Einbauzustand
FS = FSBU / L im Betriebszustand.
Die Anwendung der Gleichung a 2.9-21 kann zu sehr konservativen Ergebnissen führen, z.B. im Falle dD größer als (di + 2 ⋅ sF). Detalliertere Betrachtungen unter Berücksichtigung der Hebelarm- und Geometrieverhältnisse sind zulässig.
2.9.4.3 Vorschweißbunde mit konischem Ansatz nach Bild a 2.9-3
Die Berechnung erfolgt nach Abschnitt a 2.9.4.2 mit d´L = 0.
Bild a 2.9-3: Vorschweißbund mit konischem Ansatz
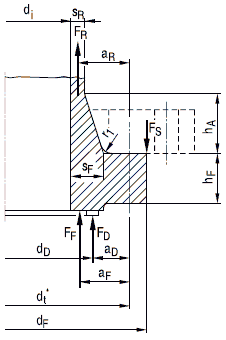
a 2.9.4.4 Flansche und Bunde mit innenliegender Dichtung und zylindrischem Ansatz nach Bild a 2.9-4 und Bild a 2.9-5
Der Flansch ist in den Querschnitten A-a und C-C zu überprüfen. Der vorhandene Flanschwiderstand im Schnitt A-a ergibt sich aus:
| (a 2.9-23) |
Der vorhandene Flanschwiderstand im Schnitt C-C ergibt sich entsprechend Abschnitt a 2.9.4.2.
Bei der Berechnung von Vorschweißbunden ist d´L = 0 zu setzen.
Bild a 2.9-4: Vorschweißflansch mit zylindrischem Ansatz
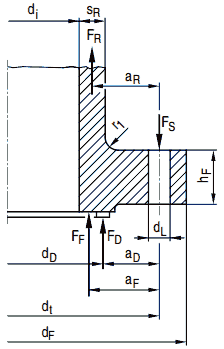
Bild a 2.9-5: Vorschweißbund mit zylindrischem Ansatz
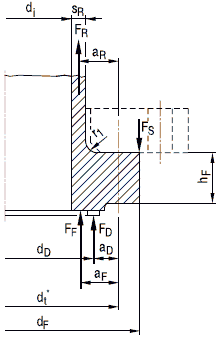
a 2.9.4.5 Losflansche nach Bild a 2.9-6
Die erforderliche Höhe des Flanschblatts beträgt
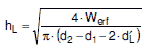 |
(a 2.9-24) |
mit Werf nach Gleichung (a 2.9-3).
Bild a 2.9-6: Losflansch
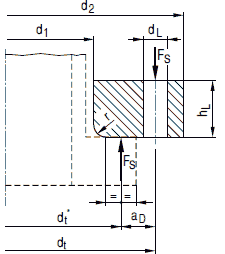
a 2.9.4.6 Deckelflansch für Reaktordruckbehälter nach den Bildern a 2.9-7 und a 2.9-8
(1) Der Flansch darf als Losflansch betrachtet werden. Zusätzlich muss jedoch die Umfangsspannung aus dem Innendruck berücksichtigt werden. Da es sich hierbei um eine Flansch-Kugelschalen-Verbindung handelt, ist die Membrankraft in ihre Komponenten zu zerlegen (siehe Bild a 2.9-7).
(2) Zur Ermittlung des Schwerpunktes ist die Fläche der Schraubenlöcher gleichmäßig über den Umfang zu verteilen und ein Ersatzdurchmesser zu bilden:
| h ⋅ n ⋅ π/4 ⋅ dL2 = π⋅ dt⋅ d´L⋅ h | (a 2.9-25) |
| d´L= n ⋅ dL2 / 4 ⋅ dt | (a 2.9-26) |
Bild a 2.9-7: Deckelflansch des Reaktordruckbehälters
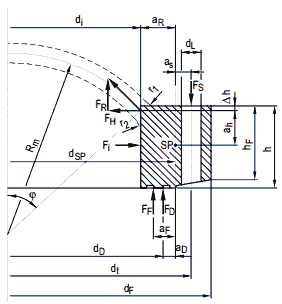
(3) Somit ergeben sich als äußere Momente:
| MS = FS × aS= FS × 0,5 × (dt - dSP) | (a 2.9-27) |
| MR = FR ⋅ aR= FR ⋅ 0,5 ⋅ (dSP- di) | (a 2.9-28) |
| MF= FF ⋅ aF= FF⋅ 2 ⋅ dSP⋅ (di+ dD) / 4 | (a 2.9-29) |
| MD = FD ⋅ aD = FD⋅ 0,5 ⋅(dSP- dD) | (a 2.9-30) |
| (a 2.9-31) |
und das gesamte Moment beträgt:
| M = MS+ MR+ MF+ MD+ MH | (a 2.9-32) |
(Vorzeichenregel: positives Vorzeichen bei Drehung im Uhrzeigersinn)
(4) Das Widerstandsmoment beträgt:
| W = π / 4 ⋅ (dF - di - 2 ⋅ d´L) ⋅ hF2 | (a 2.9-33) |
Die erforderliche Höhe des Flanschblatts beträgt demnach:
| (a 2.9-34) |
(5) Die Umfangsspannung, hervorgerufen aus Stülpung, ergibt sich aus folgender Gleichung:
| σu1= M / Wvorh. | (a 2.9-35) |
(6) Die Belastung des Flansches durch den Innendruck beträgt:
| Fi=p × di ⋅ hF ⋅ p | (a 2.9-36) |
(7) Die von der anschließenden Kugelschale ausgeübte Horizontalkraft beträgt:
| FH = FR ⋅ cot Φ | (a 2.9-37) |
(8) Die resultierende Horizontalkraft beträgt:
| Fres= Fi- FH | (a 2.9-38) |
(9) Die Wanddicke des verschwächten Flanschringquerschnitts beträgt:
| b = 0,5 ⋅ (dF- di - 2 ⋅ d´L) | (a 2.9-39) |
(10) Der resultierenden Horizontalkraft entspricht ein äquivalenter Innendruck von:
| Päq = Fres / π ⋅ di⋅ hF | (a 2.9-40) |
(11) Die mittlere Umfangsspannung folgt somit aus der nachstehenden Gleichung:
|
(a 2.9-41) |
(12) Die gesamte Spannung beträgt:
| σ = σu1+ σu2 | (a 2.9-42) |
(13) Zusätzlich ist die Flächenpressung zwischen Deckelflansch und Unterteil nachzurechnen (siehe Bild 2.9-8).
Bild a 2.9-8: Dichtfläche des Reaktordruckbehälters
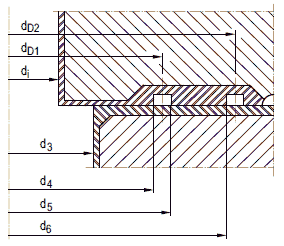
Als Dichtfläche wird nur die Fläche zwischen dem inneren Durchmesser der äußeren O-Ring-Nut und dem lichten Durchmesser des Flanschunterteils betrachtet.
Die Dichtfläche beträgt:
| (a 2.9-43) |
Die vorhandene Flächenpressung beträgt:
| pA = FSmax / A | (a 2.9-44) |
Die zulässige Flächenpressung ist in Abhängigkeit von der Werkstoffpaarung nachzuweisen.
a 2.9.5 Dimensionierung der Flansche bei Kraftnebenschlussverbindungen
(1) Bei Flanschverbindungen mit der Dichtung im Kraftnebenschluss ist eine hinreichende Steifigkeit und damit eine begrenzte Spalthöhe im Bereich der Dichtung erforderlich.
(2) Der für eine hinreichende Steifigkeit erforderliche Flanschwiderstand berechnet sich zu
| (a 2.9-45) |
Hierbei sind
| (a 2.9-46) |
fCF: Verhältnis der tatsächlichen Drehsteifigkeit des Flansches zu der nach Gleichung a 2.9-57 ermittelten rechnerischen Drehsteifigkeit
Sofern keine anderen Werte vorliegen, sind für fCFfolgende Werte anzunehmen:
fCF= 0,8 bei Flanschen mit zylindrischem Ansatz
fCF= 0,9 bei Flanschen mit konischem Ansatz
Das Stülpmoment M wird für die zu betrachtenden Fälle wie folgt bestimmt:
a) Einbauzustand
| M = ME= FDKU ⋅ aD+ FR0⋅ aR+ FZ0⋅aReib | (a 2.9.47) |
b) normaler und anomaler Betrieb sowie Prüfzustand
| M = FDKU ⋅ gKNS⋅aD+ FRx⋅ aR+ FF⋅aF+ FZx⋅aReib | (a 2.9-48) |
Die Summe der Werte für die maximalen Spaltvergrößerungen beider Flanschblätter Δs1+ Δs2muss kleiner sein als die in Formblatt a 2.10-2 vom Hersteller für die jeweilige Dichtheitsklasse angegebene zulässige Rückfederung aus der Blocklage Δh.
Bei Flanschen mit kegeligem Ansatz ist der vorhandene Flanschwiderstand W = WA nach Gleichung (a 2.9-13) zu bestimmen. Ferner gilt
| (a 2.9-49) |
Für Anschweißflansche, bei denen das Rohr oder der Mantel ohne kegeligen Übergang an das Flanschblatt anschließt, ist der vorhandene Flanschwiderstand W = WA nach Gleichung (a 2.9-23) zu bestimmen. Ferner gilt
| hB = 0,9 ⋅ ((di+ sR) ⋅ sR)0,5 | (a 2.9-50) |
(3) Der für eine hinreichende Festigkeit erforderliche Flanschwiderstand berechnet sich zu
| Werf= M / σzul | (a 2.9-51) |
a 2.9.6 Dichtheits- und Festigkeitsnachweise für Krafthauptschlussverbindungen
a 2.9.6.1 Allgemeines
(1) In der In- und Außerbetriebnahme ändert sich der Verspannungszustand infolge von Innendruck, betriebsunabhängigen Zusatzkräften und Zusatzmomenten, temperaturbedingter Änderung der E-Moduln, unterschiedlicher Wärmedehnung, Setzen von Dichtungen, insbesondere von Weichstoffdichtungen.
(2) Ausgehend von der gewählten Vorspannkraft sind unter Beachtung des elastischen Verformungsverhaltens der Flanschverbindung die Schraubenkraft und die Restdichtungskraft unter Berücksichtigung abzutragender Torsionsmomente und Querkräfte für jeden maßgebenden Lastfall zu überprüfen.
Der Mutternweg stellt bei paarigen Flanschen die Summe der Federwege der Flansche 2 ⋅ ΔF, der Schrauben ΔS, der Dichtung ΔD, im Falle von Temperatureinwirkung der unterschiedlichen Wärmedehnung von Flansch und Schraube ΔW sowie im Falle von Setzvorgängen in der Schraubenverbindung und in der Dichtung ΔVdar. Unter Berücksichtigung dieser Größen bleibt der Mutternweg im Einbauzustand E für jeden beliebigen Betriebszustand x konstant:
| 2 ⋅ ΔFE+ ΔSE+ ΔDE= 2 ⋅ ΔFx+ ΔSx+ ΔDx+ΔWx+ΔVx | (a 2.9-52) |
Bei nicht paarigen Flanschen tritt an die Stelle von 2 ⋅ ΔFdie Summe der Federwege der unterschiedlichen Einzelflansche ΔF1+ ΔF2, bei Flansch-Deckel-Verbindungen tritt an die Stelle von 2 ⋅ ΔFdie Summe der Federwege von Flansch und Deckel ΔF + ΔB.
Bei Flanschverbindungen mit Dehnhülsen sind auch deren Steifigkeiten zu berücksichtigen.
(3) Mit den sich aus der Nachprüfung der Kraft- und Verformungsverhältnisse der maßgebenden Lastfälle maximal ergebenden Schrauben- und Dichtungskräften ist der Festigkeitsnachweis der gesamten Flanschverbindung (Flansch, Blinddeckel, Schrauben und Dichtung) zu kontrollieren.
(4) Die zulässigen Spannungen für Flansche sind der Tabelle a 2.9-1 lfd. Nr. 4 zu entnehmen. Bei der Bestimmung der Widerstandmomente sind neben diesen zulässigen Spannungen in der Gleichung a 2.9-10 die Kraft FRxund in der Gleichung a 2.9-20 die Kraft FSBxzugrunde zu legen.
(5) Eine allgemeine Vorgehensweise für die Führung der Dichtheits- und Festigkeitsnachweise für Flanschverbindungen mit der Dichtung im Krafthauptschluss zeigt Bild a 2.9-9.
(6) Die für die Berechnung der betrieblichen Belastungen erforderliche Vorspannkraft der Schrauben ist zuerst nach Abschnitt a 2.8.4.1 zu bestimmen (FS0= FS0U), auch wenn keine Dimensionierung erforderlich ist.
(7) Für die Vorspannkraft der Schrauben ist die Dichtungsflächenpressung im Einbauzustand σv zu berechnen, mit der die Mindestflächenpressung im Betriebszustand für die geforderte Dichtheitsklasse σBU / L bestimmt wird, siehe Abschnitt a 2.10.2.
(8) Werden die einzelnen Bedingungen in Bild 2.9-9 nicht erfüllt, dann ist entsprechend iterativ vorzugehen.
a 2.9.6.2 Vereinfachtes Verfahren zur Nachprüfung der Kraft- und Verformungsverhältnisse
a 2.9.6.2.1 Allgemeines
(1) In den folgenden Abschnitten sind für einige Fälle der Einwirkung von Innendruck, Zusatzkräften und Zusatzmomenten, temperaturbedingter Änderung der E-Moduln, unterschiedlicher Wärmedehnung in Flansch und Schrauben sowie Setzvorgängen in der Dichtung Gleichungen zur angenäherten Ermittlung der Schraubenkräfte FS, der Dichtungskräfte FD, sowie der Verformungen ΔF, ΔSund ΔDin den betreffenden Zuständen angegeben.
(2) Alternativ hierzu darf zur detaillierteren Erfassung
eine angenäherte Nachprüfung des Kraft- und Verformungsverhaltens nach anderen Verfahren erfolgen.
a 2.9.6.2.2 Berechnung der Federsteifigkeiten
a 2.9.6.2.2.1 Schrauben
Die elastische Längung der Schrauben darf berechnet werden aus
| ΔS = FS / cS | (a 2.9-53) |
Für Starrschrauben gilt annähernd
|
(a 2.9-54) |
Für Dehnschrauben gilt
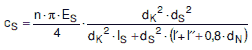 |
(a 2.9-55) |
Bild a 2.9-9: Nachweisführung für Flanschverbindungen mit Dichtungen im Krafthauptschluss (schematisch)
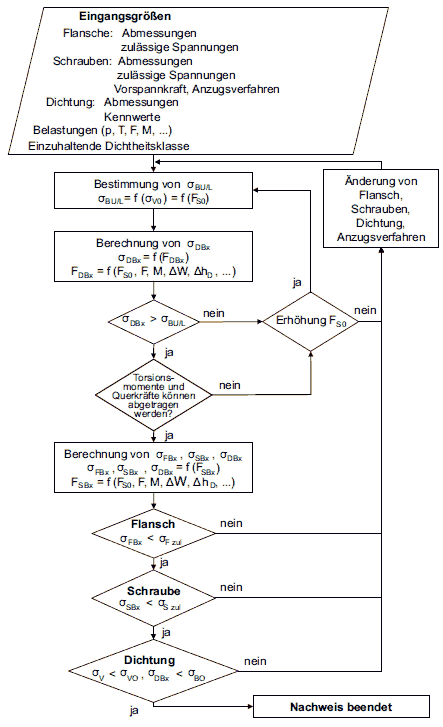
Bild a 2.9-10: Schrauben
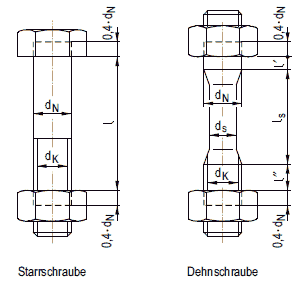
a 2.9.6.2.2.2 Flansche
Die elastische Durchbiegung ΔFdes Einzelflansches beträgt im Schraubenlochkreis
| ΔF = M ⋅ aD / CF | (a 2.9-56) |
Bei der Berechnung der Verspannung paariger Flansche muss ΔF stets doppelt eingesetzt werden.
|
(a 2.9-57) |
Bei Flanschen mit kegeligem Ansatz ist W = WA nach Gleichung (a 2.9-13).
Hinweis:
Von einem kegeligen Ansatz wird ausgegangen, wenn die Bedingungen
0,2< sF ⋅ sR / hA< 0,5
und
ha / hF> 0,5
eingehalten sind. Ferner gilt
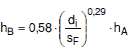 |
(a 2.9-58) |
Für Anschweißflansche, bei denen das Rohr oder der Mantel ohne kegeligen Übergang an das Flanschblatt anschließt, gilt
| W = π / 4 ⋅ [(dF - di - 2 ⋅ d´L) ⋅ hF2 + (di + sR) ⋅ (sR2 -s12)] | (a 2.9-59) |
Ferner gilt
| hB= 0,9 ⋅ ((di+ sR) ⋅sR)0,5 | (a 2.9-60) |
Für Losflansche gilt
| W = π / 4 ⋅ [(d2 - di - 2 ⋅ d´L) ⋅ hL2 | (a 2.9-61) |
a 2.9.6.2.2.3 Blinddeckel
Die elastische Durchbiegung ΔB des Blinddeckels beträgt im Schraubenlochkreis für den Einbauzustand 0:
| ΔB0= FS0 / cB0 | (a 2.9-62) |
mit FS0= FD0: Einbauschraubenkraft
und cB0: Federsteifigkeit im Einbauzustand
und für den Betriebszustand x:
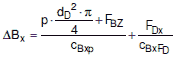 |
(a 2.9-63) |
wobei die Deckelkraft FBx
| (a 2.9-64) |
sein muss und
cBxp= Federsteifigkeit für die Belastung durch die Deckelkraft
und
EBT= Federsteifigkeit für die Belastung
cBxFD=cB,0⋅ EBT / EBRT durch die Dichtungskraft FDx
Die Federsteifigkeiten für die unterschiedlichen Belastungsarten der Blinddeckel dürfen z.B.
entnommen oder mittels geeigneter Methoden ermittelt werden.
a 2.9.6.2.2.4 Dichtungen
Der elastische Anteil der Zusammendrückung (Rückfederung) der Dichtung ΔD kann für Flachdichtungen wie folgt angenommen werden
| ΔD= FD / cD | (a 2.9-65) |
wobei
| cD= ED ⋅ π ⋅ dD ⋅bD /hD | (a 2.9-66) |
Hierbei ist je nach Lastfall EDder E-Modul des Dichtungswerkstoffes bei Einbau- oder Betriebstemperatur.
Bei Metalldichtungen aller Art ist die Rückfederung im Vergleich zur Durchbiegung der Flansche so gering, dass sie vernachlässigt werden kann.
a 2.9.6.2.2.5 Wärmedehnungsunterschiede und Setzbeträge
In den Gleichungen zur Berechnung der Schrauben- und Dichtungskräfte gemäß Abschnitt a 2.9.6.2.3 können auch Wärmedehnungsunterschiede zwischen Flansch, Blinddeckel, Schrauben und Dichtung sowie Setzbeträge berücksichtigt werden:
| ΔWx= Ik⋅ αS⋅ (TSx-20° ) - hF1⋅αF1 ⋅ (TF1x - 20° ) - hF2⋅ αF2⋅ (TF2x -20°) - hD⋅ αD⋅ (TDx - 20°) | (a 2.9-67) |
mit
ΔWx: Differenz der thermischen Längenänderungen von Flansch, Blinddeckel, Schrauben und Dichtung. Die Indizes 1 und 2 beziehen sich auf den Flansch und den zugehörigen Gegenflansch oder Blinddeckel
Ik: Klemmlänge der Schrauben
(ΔhD)x : Setzbetrag der Dichtung (ist nur bei Weichstoffdichtungen und Metall-Weichstoffdichtungen zu berücksichtigen; hierbei ist von den Angaben des Herstellers auszugehen.)
a 2.9.6.2.3 Berechnung der Schrauben- und Dichtungskräfte
a 2.9.6.2.3.1 Paarige Flanschverbindungen
Für paarige Flanschverbindungen gilt:
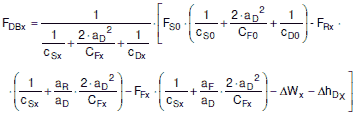 |
(a 2.9-68) |
| FSBx = FDBx + FRx + FFx | (a 2.9-69) |
a 2.9.6.2.3.2 Nichtpaarige Flanschverbindungen
Für Flanschverbindungen mit nichtpaarigen Flanschen 1 und 2 gilt:
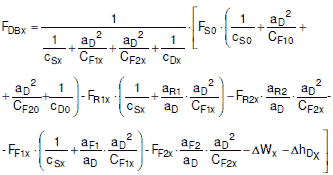 |
(a 2.9-70) |
| FSBx= FDBx+ FRx+ FFx | (a 2.9-71) |
und
| FR1x+ FF1x= FR2x+ FF2x | (a 2.9-72) |
a 2.9.6.2.3.3 Flansch-Blinddeckel
Für die Verbindung Flansch-Blinddeckel gilt:
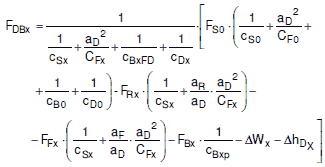 |
(a 2.9-73) |
| und
FSx= FDBx+ FRx+ FFx |
(a 2.9-74) |
a 2.9.7 Dichtheits- und Festigkeitsnachweise für Kraftnebenschlussverbindungen
a 2.9.7.1 Allgemeines
(1) Zur Gewährleistung der geforderten Eigenschaften der Flanschverbindung mit der Dichtung im Kraftnebenschluss muss die Blocklage bei allen relevanten Belastungen beibehalten werden (FKontakt> 0).
(2) Die Dichtung überträgt nur einen Teil der Vorspannkraft.
(3) Abhängig von der geometrischen Gestaltung kann es zwischen Erreichen der Blocklage und den Betriebszuständen zu einer Vergrößerung des Spalts im Dichtungsbereich kommen. Diese Vergrößerung muss durch das Rückfederungs- vermögen der Dichtung Δh (siehe Formblatt a 2.10-2) kompensiert werden können.
Hinweis:
Die Bewertung der Vergrößerung der Spalthöhe erfolgt auf der Grundlage einer für den gewählten Dichtungstyp repräsentativen Rückverformungskurve. Die Vergrößerung der Spalthöhe zwischen dem Einbauzustand (Erreichen der Blocklage) und den Betriebszuständen wird bei Dichtungsdicken von 4,5 mm und Nuttiefen von 3,3 mm üblicherweise mit 0,1 mm begrenzt (sofern in Formblatt a 2.10-2 keine anderen Angaben enthalten sind), da das Abdichtverhalten von Spiraldichtungen und Graphit-Profilringen bis zu einer Rückfederung der Dichtung dieser Größe nur unwesentlich beeinträchtigt ist (siehe Literatur [9] und [10]).
(4) Bei Änderungen des Spalts (z.B. durch unterschiedliche Wärmedehnungen der verspannten Teile oder durch Rohrleitungslasten) kann ein Entlasten der Dichtung hervorgerufen werden. Die dadurch bedingte Änderung der Leckagerate darf mit der errechneten Entlastung nach Bild a 2.10-5 und den Angaben entsprechend Formblatt a 2.10-2 bestimmt werden.
(5) Eine allgemeine Vorgehensweise für die Führung der Dichtheits- und Festigkeitsnachweise für Flanschverbindungen mit der Dichtung im Kraftnebenschluss zeigt Bild a 2.9-11.
(6) Die Leckagerate der Verbindung ist mit der errechneten Dichtungsflächenpressung σDBnach Bild a 2.10-1 zu bestimmen. Diese Leckagerate muss kleiner sein als die der geforderten Dichtheitsklasse L zugeordnete, sonst ist eine andere Dichtung zu wählen, und die vorherigen Schritte (Steifigkeitsnachweis, Bestimmung der Schraubenkraft) sind zu wiederholen.
(7) Werden die einzelnen Bedingungen in Bild a 2.9-11 nicht erfüllt, dann ist entsprechend iterativ vorzugehen.
a 2.9.7.2 Vereinfachtes Verfahren zur Nachprüfung der Kraft- und Verformungsverhältnisse
a 2.9.7.2.1 Allgemeines
(1) In den folgenden Abschnitten sind für einige Fälle der Einwirkung von Innendruck, Zusatzkräften und Zusatzmomenten, temperaturbedingter Änderung der E-Moduln, unterschiedlicher Wärmedehnung in Flansch und Schrauben sowie Setzvorgängen Gleichungen zur angenäherten Ermittlung der Schraubenkräfte FS, der Dichtungskräfte FD, der Flanschmomente M sowie der Spaltvergrößerung Δs in den betreffenden Zuständen angegeben.
(2) Alternativ hierzu darf zur detaillierteren Erfassung
eine angenäherte Nachprüfung des Kraft- und Verformungsverhaltens nach anderen Verfahren erfolgen.
a 2.9.7.2.2 Eingabewerte
(1) Die Bestimmung der Wärmedehnungsunterschiede ΔWx(mit Ausnahme der Dichtung) sowie die Bestimmung der Federsteifigkeiten für Schrauben und Blinddeckel hat nach Abschnitt a 2.9.6.2.2 zu erfolgen. Die Federsteifigkeiten für Flansche sind nach Abschnitt a 2.9.6.2.2.2 unter Berücksichtigung der Abminderungsfaktoren fCF(siehe Abschnitt a 2.9.5 Absatz 2) zu berechnen.
(2) Die erforderliche Kraft zum Erreichen der Blocklage FDKUist nach Gleichung (a 2.8-17) zu bestimmen.
(3) Die Federsteifigkeit der Kraftnebenschlussdichtung ist aus der Rückfederungskurve der Dichtung oder dem Formblatt a 2.10-2 wie folgt abzuleiten:
| cDKNS= π ⋅ dD ⋅ bD ⋅EDKNS / hD | (a 2.9-75) |
Hierbei ist je nach LastfallEDKNS der E-Modul des Dichtungswerkstoffes bei Einbau- oder Betriebstemperatur.
(4) Als Hebelarm der Kontaktkräfte aKontaktdarf der Abstand von Schraubenmitte zur äußeren Kontaktstelle der beiden Flansche aMangesetzt werden. Beim Losflansch ist dies der Abstand von Schraubenmitte bis zum Bundaußendurchmesser dF. Eine genauere Berechnung nach folgender Berechnungsgleichung ist zulässig (iteratives Vorgehen mit dem Anfangswert aKontakt= aMbei der Bestimmung der Kraft FKontakt 0):
| aKontakt= aM+ FKontakt 0 / 2 ⋅ dM ⋅π ⋅ RmRT | (a 2.9-76) |
Bei ungleichen Flanschwerkstoffen ist als Zugfestigkeit RmRTdie Zugfestigkeit des schwächeren Flanschwerkstoffs einzusetzen.
Bild a 2.9-11: Nachweisführung für Flanschverbindungen mit Dichtungen im Kraftnebenschluss (schematisch)
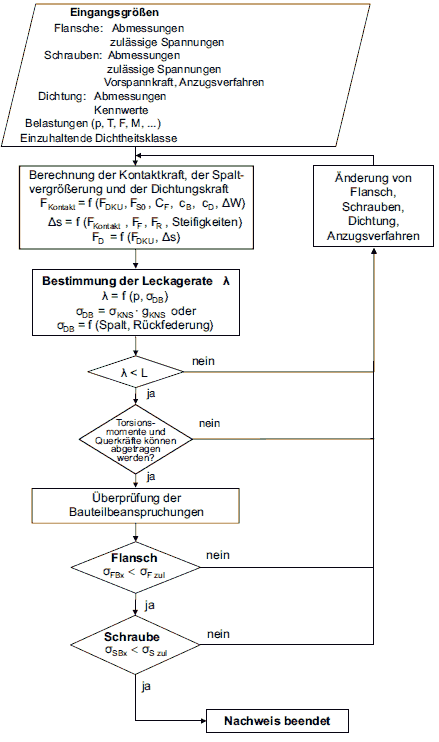
a 2.9.7.2.3 Paarige Flanschverbindungen
a 2.9.7.2.3.1 Einbauzustand
| xS0= FS0 / cS0 | (a 2.9-77) | |||||||||||||||
| γFKNS= FDKU ⋅ aD /CF0 | (a 2.9-78) | |||||||||||||||
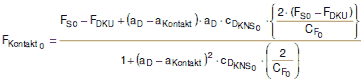 |
(a 2.9-79) | |||||||||||||||
|
(a 2.9-80) | |||||||||||||||
| FD0 = FDKU- } | (a 2.9-81) |
Spaltvergrößerung am Dichtungsdurchmesser dD:
| Δs0 = 2 ⋅ (aD - aKontakt) ⋅ (γF0- γFKNS) | (a 2.9-82) |
Flanschmoment:
| M0= γF0 ⋅ CF0 | (a 2.9-83) |
a 2.9.7.2.3.2 Betriebszustand
|
(a 2.9-84) |
| FKontaktx = - γFx⋅ b1 + d1 | (a 2.9-85) |
mit den Koeffizienten
| b1= 2 ⋅ cSx ⋅ aKontakt- 2 ⋅ (aD- aKontakt) ⋅ CDKNSx | (a 2.9-86) |
| d1 = 2 ⋅cSx ⋅ aKontakt ⋅γF0- gKNS⋅ FDKU- 2 ⋅γFKNS⋅ (aD - aKontakt) ⋅ cDKNSx- FR1- FF1+ cSx ⋅ (xS0- ΔWx) | (a 2.9-87) |
| a2= aD- aKontakt | (a 2.9-88) |
| b2= CF1x + 2 ⋅ cSx⋅ aKontakt⋅ aD | (a 2.9-89) |
| d2= cSx⋅ 2 ⋅ γF0⋅ aKontakt⋅ aD+ FR⋅ (aR- aD) + FF ⋅ (aF- aD) + cSx⋅ (xS0- ΔWx) ⋅ aD | (a 2.9-90) |
| FDx= gKNS ⋅ FDKU- {2 ⋅ (γFx- γFKNS)} ⋅ (aD- aKontakt) ⋅ cDKNSx | (a 2.9-91) |
| FSx = FKontaktx + FDx + FR + FF | (a 2.9-92) |
Spaltvergrößerung am mittleren Dichtungsdurchmesser dD:
| ΔSx= 2 ⋅ (aD- aKontakt) ⋅ (γFx- γFKNS) | (a 2.9-93) |
Flanschmoment:
| Mx= γFx ⋅ CFx | (a 2.9-94) |
a 2.9.7.2.4 Nicht paarige Flanschverbindungen
a 2.9.7.2.4.1 Einbauzustand
| xS0= FS0 / cS0 | (a 2.9-95) | |||||||||||||||
| γF1KNS= FDKU⋅ aD / CF10 | (a 2.9-96) | |||||||||||||||
| γF2KNS= FDKU⋅ aD / CF20 | (a 2.9-97) | |||||||||||||||
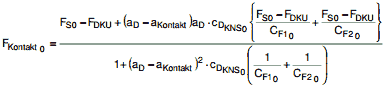 |
(a 2.9-98) | |||||||||||||||
|
(a 2.9-99) | |||||||||||||||
|
(a 2.9-100) | |||||||||||||||
| FD0= FDKU- { (γF1 0 - γF1 KNS) + (γF2 0 - γF2KNS) ⋅ (aD- aKontakt)} ⋅ cDKNS0 | (a 2.9-101) |
Spaltvergrößerung am Dichtungsdurchmesser dD:
| Δs0= (aD- aKontakt) ⋅ { (γF1 0- γF1 KNS) + (γF2 0- γF2KNS)} | (a 2.9-102) |
Flanschmomente:
| M1 0= γF1 0 ⋅ CF1 0 | (a 2.9-103) |
| M2 0= γF2 0⋅ CF2 0 | (a 2.9-104) |
a 2.9.7.2.4.2 Betriebszustand
|
(a 2.9-105) | ||||||||||||
|
(a 2.9-106) | ||||||||||||
| FKontakt x= - γF1x⋅ b1- γF2x⋅ b1+ d1 | (a 2.9-107) |
mit den Koeffizienten
| b1= cSx⋅ aKontakt- (aD- aKontakt) ⋅cDKNSx | (a 2.9-108) |
| d1= cSx ⋅ aKontakt(γF1 0+ γF2 0) - gKNS⋅ FDKU- γF1KNS⋅ (aD- aKontakt) ⋅ cDKNSx- γF2KNS⋅ (aD- aKontakt) ⋅ cDKNSx- FR1- FF1+ cSx⋅ (xS0- ΔWx) | (a 2.9-109) |
| a2= aD- aKontakt | (a 2.9-110) |
| b2= CF1 x + cSx ⋅aKontakt⋅ aD | (a 2.9-111 ) |
| c2= cSx⋅ aKontakt ⋅ aD | (a 2.9-112) |
| d2= cSx ⋅ (γF1 0+ γF2 0) ⋅ aKontakt⋅ aD+ FR1 ⋅ (aR1- aD) + FF1⋅ (aF1- aD) + cSx⋅ (xS0- ΔWx) ⋅ aD | (a 2.9-113) |
| c3= CF2x+ cSx⋅ aKontakt⋅ aD | (a 2.9-114) |
| d3= cSx⋅ (γF1 0+ γF2 0) ⋅ aKontakt⋅ aD+ FR2⋅ (aR2- aD) + FF2⋅ (aF2- aD) + cSx ⋅ (xS0- ΔWx) ⋅ aD | (a 2.9-115) |
| FDx= gKNS⋅ FDKU- {(γF1x- γF1KNS) + (γF2x- γF2KNS)} ⋅ (aD - aKontakt) ⋅ cDKNSx | (a 2.9-116) |
| FSx = FKontakt x + FDx +FR1 + FF1 | (a 2.9-117) |
Spaltvergrößerung am Dichtungsdurchmesser dD:
| Δsx= (aD- aKontakt) ⋅ {(γF1x- γF1KNS) + (γF2x- γF2KNS)} | (a 2.9-118) |
Flanschmomente:
| M1x= γF1x⋅ CF1x | (a 2.9-119) |
| M2x= γF2x⋅ CF2x | (a 2.9-120) |
a 2.9.7.2.5 Flansch-Blinddeckel-Verbindungen
Es gelten (mit Ausnahme der Bestimmungsgleichungen für die Flanschmomente am 2. Flansch) die Gleichungen für nicht paarige Flanschverbindungen gemäß Abschnitt a 2.9.7.2.4 mit den nachfolgenden Ersatzgrößen zur Abbildung des Blinddeckels als 2. Flansch.
| CF20 = cB0 ⋅ aD2 | (a 2.9-121) |
| CF2x = (E υ / E20) ⋅ cB0 ⋅ aD2 | (a 2.9-122) |
| FR2= p ⋅ 1 / 4 ⋅p × dD2+ FBZ | (a 2.9-123) |
| aR2 = aD⋅ cBxFD / cBxp | (a 2.9-124) |
| FF2= 0 | (a 2.9-125) |
Die Überprüfung der Festigkeit des Blinddeckels erfolgt mit den Lasten FD0und FKontakt 0im Einbauzustand sowie FKontakt x, FDx, p und FBZim Betriebszustand.
a 2.10 Dichtungen
a 2.10.1 Allgemeines
(1) Für die Berechnungsgrößen und Einheiten gelten die Festlegungen in den Abschnitten a 2.8.1 und a 2.9.1.
(2) Die Dichtungskennwerte sind gemäß den Formblättern a 2.10-1 und a 2.10-2 bereitzustellen.
Hinweis:
Verfahren zur Ermittlung der Dichtungskennwerte sind in [11] enthalten.
a 2.10.2 Berechnungskennwerte für KHS-Verbindungen Hinweis:
Die Definition der Dichtungskennwerte ist in DIN 28090-1 (1995-09) und in DIN EN 13555 (2005-02) enthalten.
a 2.10.2.1 Mindestflächenpressung im Einbauzustand σVU / L
Die Mindestflächenpressung σVU / List die Flächenpressung, die von der Einbauschraubenkraft FS0 auf die wirksame Dichtfläche (gepresste Dichtungsfläche) AD = π ⋅ dD× bD ausgeübt werden muss, damit sich durch Anpassung an die Flanschrauheiten und Verkleinern innerer Hohlräume die geforderte Dichtheit im Betriebszustand ergibt. Ein Beispiel für die Bestimmung der Kennwerte für die Abdichteigenschaften (σVU / L, σBU / L) zeigt Bild a 2.10-1.
Bild a 2.10-1: Bestimmung der Kennwerte zur Beurteilung der Abdichteigenschaften (schematisch)

Die dem Kennwert σVU / Lzugrunde liegende Dichtheitsklasse wird im Index genannt, z.B. σVU / 0,1 für die Dichtheitsklasse L0,1 mit einer spezifischen Leckagerate λ< 0,1 mg / (s ⋅ m).
σVU / Lbestimmt somit die minimal erforderliche Dichtungskraft im Einbauzustand FDVU= AD ⋅ σVU / Lfür eine bestimmte Dichtheitsklasse L. Eine mögliche Zuordnung der Dichtheitsklassen zum verwendeten Medium zeigt Tabelle a 2.10-1.
Hinweis:
(1) Zur Bestimmung der wirksamen Dichtungsfläche siehe die Bilder a 2.10-2 und a 2.10-3.
(2) Die Dichtungsbreite bD von Schmiegungsdichtungen nach Bild a 2.10-3 ermittelt sich aus Berechnungsansätzen nach DIN EN 1591-1 (2009-10) "Flansche und Flanschverbindungen - Regeln für die Auslegung von Flanschverbindungen mit runden Flanschen und Dichtung - Teil 1: Berechnungsmethode; Deutsche Fassung EN 1591-1:2001+A1:2009", DIN 2696 (1999-08) "Flanschverbindungen mit Dichtlinse" oder Herstellerangaben unter Verwendung der zum jeweiligen Berechnungsverfahren gehörenden Dichtungskennwerte.
Bild a 2.10-2: Darstellung der Dichtungsbreite bD
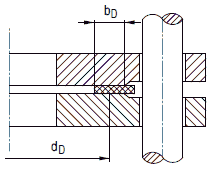
Bild a 2.10-3: Dichtungsprofile für Schmiegungsdichtungen
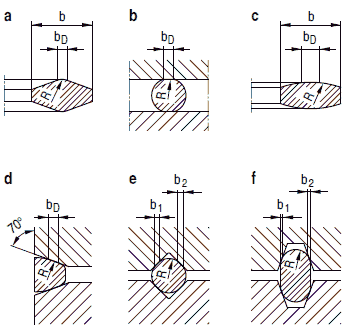
Bild a 2.10-4: Winkel α bei Schmiegungsdichtungen, dargestellt am Beispiel einer Linsendichtung
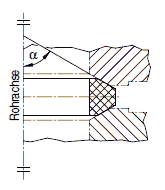
Formblatt a 2.10-1: Zusammenstellung der Dichtungskennwerte (Muster)
| Dichtungskennwerte für Dichtungen1 im Krafthauptschluss | |||||||||||||||||||
| Hersteller: | Bezeichnung: | ||||||||||||||||||
| Abdichteigenschaften (σVU / L, σBU / L) | |||||||||||||||||||
| Abmessung der Prüflinge: | |||||||||||||||||||
| Prüfmedium2 | ...................... | ...................... | ...................... | ...................... | |||||||||||||||
| Dichtheitsklasse | ...................... | ...................... | ...................... | ...................... | |||||||||||||||
| Innendruck in MPa3 | ...................... | ...................... | ...................... | ...................... | |||||||||||||||
| Kennwerte in MPa4 | σVU / L; σV | σBU / L | σVU / L; σV | σBU / L | σVU / L; σV | σBU / L | σVU / L; σV | σBU / L | |||||||||||
| Verformungseigenschaften (σVO, σBO, ED, ΔhD) | |||||||||||||||||||
| Abmessung der Prüflinge: | |||||||||||||||||||
| σVObzw. σBOin MPa5 | RT | 100 °C | 200 °C | 300 °C | 400 °C | ||||||||||||||
| ED (σV= ....... MPa) | |||||||||||||||||||
| ED (σV= ....... MPa) | |||||||||||||||||||
| ED (σV= ....... MPa) | |||||||||||||||||||
| ED (σV= ....... MPa) | |||||||||||||||||||
| Abmessung der Prüflinge: | |||||||||||||||||||
| σ in MPa6 | RT | 100 °C | 200 °C | 300 °C | 400 °C | ||||||||||||||
| C1 | C2 | C1 | C2 | C1 | C2 | C1 | C2 | C1 | C2 | ||||||||||
| ΔhD in mm | |||||||||||||||||||
| C : Steifigkeiten von Druckstandsprüfeinrichtungen C1=kN / mm C2 = kN / mm | |||||||||||||||||||
| 1) Bei Dichtungsplatten sind noch Angaben zu dem Einfluss von Dichtungsabmessungen (hD, bD) erforderlich.
2) Als Prüfmedium ist Stickstoff oder Helium zu wählen. Die Dichtheitsklasse und die Innendruckstufe ist nach Anforderung des Anwenders zu wählen. 3) Die Innendruckstufen sind vorzugsweise 1, 2, 4, 8 und 16 MPa. Bei Zwischenwerten sind stets die Dichtungskennwerte der nächsthöheren Druckstufe zu verwenden. 4) σBU / List in Abhängigkeit von σV> σVU / Lanzugeben. Alternativ dürfen auch grafische Darstellungen angegeben werden. 5) Bei Dichtungen, bei denen das Kriechrelaxationsverhalten einen wesentlichen Einfluss hat, können diese Kennwerte nur in Zusammenhang mit ΔhDbetrachtet werden. 6) Ausgangsflächenpressung |
|||||||||||||||||||
Formblatt a 2.10-2: Zusammenstellung der Dichtungskennwerte (Muster)
| Dichtungskennwerte für Dichtungen im Kraftnebenschluss | |||||||||||
| Hersteller: | Bezeichnung: | ||||||||||
| Abdichteigenschaften (pKNS / L) | |||||||||||
| Abmessung der Prüflinge: | Abmessungen der Nut: | ||||||||||
| Prüfmedium: | |||||||||||
| Innendruck1 in MPa | Leckagerate λ in mg / (m ⋅ s) | ||||||||||
| σKNS= ..... MPa und Δh = ..... mm | 0,8 ⋅ σKNS= ..... MPa und Δh = ..... mm | ..... ⋅ σKNS= ..... MPa und Δh = ..... mm | . . | ||||||||
| 1 | |||||||||||
| 2 | |||||||||||
| 4 | |||||||||||
| 8 | |||||||||||
| 16 | |||||||||||
| Verformungseigenschaften (σKNS, gKNS, EDKNS) | |||||||||||
| Abmessung der Prüflinge: | Abmessungen der Nut: | ||||||||||
| RT | |||||||||||
| σKNSin MPa | |||||||||||
| Abmessung der Prüflinge: | Abmessungen der Nut: | ||||||||||
| RT | 100 °C | 200 °C | 300 °C | 400 °C | |||||||
| gKNS | |||||||||||
| Abmessung der Prüflinge: | Abmessungen der Nut: | ||||||||||
| Rückfederung Δh in mm | EDKNS(RT) in MPa | EDKNS(100 °C) in MPa | EDKNS(200 °C) in MPa | EDKNS(300 °C) in MPa | EDKNS(400 °C) in MPa | ||||||
| Δh: Rückfederung aus der Blocklage | |||||||||||
| 1) Es sind stets die Dichtungskennwerte der nächsthöheren Druckstufe zu verwenden. | |||||||||||
Tabelle a 2.10-1: Beispiele für die Zuordnung der Dichtheitsklassen und der Medien
| Dichtheitsklasse | Leckagerate bei der Dichtungsprüfung mit den Prüfmedien He oder N2mg / (m ⋅ s) | Medium |
| L1,0s | 1 | Wasser ohne Aktivität |
| L0,1 | 10-1 | a) Wasser aktivitätsführend
b) Wasserdampf ohne Aktivität c) Druckluft |
| L0,01 | 10-2 | Wasserdampf aktivitätsführend |
a 2.10.2.2 Höchstflächenpressung im Einbauzustand σVO
Die Höchstflächenpressung im Einbauzustand σVOist die maximale Flächenpressung, die von der Einbauschraubenkraft FS0 auf die wirksame Dichtfläche AD= π ⋅ dD× bDausgeübt werden darf, um eine unzulässige Entspannung der Dichtverbindung durch Zerstörung (Stauchversuch) oder durch Fließen bzw. Kriechen (Druckstandversuch) der Dichtung zu vermeiden. Sie bestimmt die maximal zulässige Dichtungskraft im Einbauzustand FDVO= AD ⋅ σVObei Raumtemperatur.
a 2.10.2.3 Mindestflächenpressung im Betriebszustand σBU / L
Die Mindestflächenpressung im Betriebszustand σBU / List die Flächenpressung, die im Betriebszustand auf die wirksame Dichtfläche AD= π ⋅ dD⋅ bDausgeübt werden muss, um die angestrebte Dichtheitsklasse bei gegebenem Medium, Innendruck und gegebener Temperatur zu erreichen.
Der Kennwert σBU / List in Abhängigkeit von der Dichtungsflächenpressung im Einbauzustand zu bestimmen.
Die dem Kennwert σBU / Lzugrundeliegende Dichtheitsklasse wird im Index genannt, z.B. σBU / 0,1 für die Dichtheitsklasse L0,1mit einer spezifischen Leckagerate λ< 0,1 mg / (s ⋅ m).
σBU / Lbestimmt somit die minimal erforderliche Dichtungskraft im Betriebszustand FDBU= AD ⋅ σBU / Lfür eine bestimmte Dichtheitsklasse.
a 2.10.2.4 Höchstflächenpressung im Betriebszustand σBO
Die Höchstflächenpressung im Betriebszustand σBO ist die maximale Flächenpressung, die unter allen möglichen Betriebsbedingungen auf die wirksame Dichtfläche AD= π ⋅ dD⋅ bDausgeübt werden darf, um eine unzulässige Entspannung der Dichtverbindung durch Strukturschädigung oder Kriechen der Dichtung zu vermeiden. σBObestimmt die maximal zulässige Dichtungskraft FDBO= AD⋅ σBObei Betriebstemperatur.
a 2.10.2.5 Setzbetrag ΔhD und Dichtungskennwert PQR
(1) Der Setzbetrag ΔhD ist die Dickenänderung einer Dichtung unter Betriebsbedingungen nach abgeschlossenem Einbau.
Hinweis:
Bei bekannter Steifigkeit des verspannten Systems lässt sich mittels ΔhDder Dichtkraftverlust abschätzen.
(2) Der Dichtungskennwert PQRist ein Faktor zur Berücksichtigung des Relaxationseinflusses auf die Dichtungsbelastung nach dem Anziehen der Schrauben und der Langzeitwirkung der Betriebstemperatur.
(3) Zur Nachprüfung des Kraft- und Verformungsverhältnisses gemäß Abschnitt a 2.9.6 ist der Kennwert PQRgemäß DIN EN 13555 Abschnitt 8.6 in einen Setzbetrag ΔhDumzurechnen.
a 2.10.2.6 Ersatz-Elastizitätsmodul ED
Der Ersatz-Elastizitätsmodul ED beschreibt das Rückverformungsverhalten der Dichtung. Bei Dichtungen mit nichtlinearer Rückverformung wird ED definiert als Sekantenmodul der Rückverformungskurve. Die in der Berechnung verwendeten Werte für den Ersatz-Elastizitätsmodul ED müssen auf die Ausgangsdicke der Dichtung bezogen sein (wie nach DIN 28090-1).
a 2.10.3 Berechnungskennwerte für KNS-Verbindungen
a 2.10.3.1 Mindestflächenpressung für KNS-
Die Mindestflächenpressung σKNSist die Flächenpressung, die von der Einbauschraubenkraft ausgeübt werden muss, um KNS einzustellen.
a 2.10.3.2 Abdichtbarer Druck bei KNS-
Der abdichtbare Druck pKNS / List der Innendruck, der bei KNS abgedichtet werden kann, ohne dass eine vorzugebende Leckagerate überschritten wird.
a 2.10.3.3 Relaxationsfaktor bei KNS-
Der Relaxationsfaktor gKNSgibt an, um wieviel Prozent die Flächenpressung bei KNSfür die gegebene Betriebstemperatur und eine für die Betriebszeit repräsentative Zeitdauer abfällt.
Hinweis:
Siehe auch Bild a 2.10-5.
a 2.10.3.4 Ersatzelastizitätsmodul ED,KNS
Der Ersatz-Elastizitätsmodul ED,KNSbeschreibt das Rückverformungsverhalten der Dichtung für verschiedene Rückfederungen der Dichtung aus der Blocklage. ED,KNSwird definiert als Sekantenmodul der Rückverformungskurve. Die in der Berechnung verwendeten Werte für den Ersatz-Elastizitätsmodul ED,KNSmüssen auf die Ausgangsdicke der Dichtung bezogen sein.
Bild a 2.10-5: Bestimmung der Leckagerate (oben) und des abdichtbaren Drucks (unten) für Flanschverbindungen mit der Dichtung im Kraftnebenschluss (schematisch)
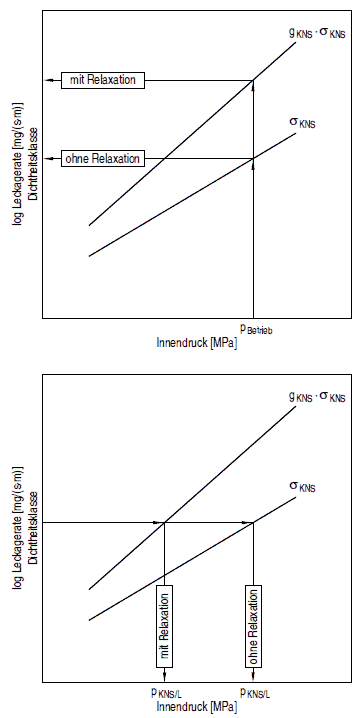
a 3 Armaturen
a 3.1 Armaturengehäuse
a 3.1.1 Berechnungsgrößen und Einheiten zu Abschnitt a 3.1
| Formelzeichen | Berechnungsgröße | Einheit |
| a, a1, a2 | Abstand | mm |
| b1, b2 | lichte Weiten unrunder Querschnitte | mm |
| c1,c2 | Zuschläge zur Wanddicke | mm |
| dAi | Innendurchmesser des Ausschnittes | mm |
| dHi | Innendurchmesser des Hauptkörpers | mm |
| l | Länge des Übergangsbereiches vom kreisförmigen zum elliptischen Querschnitt | mm |
| e, l´ | Störbereichslänge | mm |
| eA | mittragende Länge im Ausschnitt | mm |
| eH | mittragende Länge im Hauptkörper | mm |
| s0 | rechnerisch erforderliche Wanddicke ohne Zuschläge | mm |
| sA0 | rechnerisch erforderliche Wanddicke eines Abzweigs ohne Zuschläge | mm |
| sAn | Nennwanddicke des Abzweiges | mm |
| sH0 | rechnerisch erforderliche Wanddicke des Grundkörpers ohne Zuschläge | mm |
| sHn | Nennwanddicke des Hauptkörpers | mm |
| s2H | Wanddicke am Übergang vom Flansch zur Kugelschale | mm |
| sn | Nennwanddicke | mm |
| sRn | Nennwanddicke des Rohres | mm |
| y | zylindrischer Anteil in Ovalkörpern | mm |
| Ap | drucktragende Fläche | mm2 |
| Aσ | tragende Querschnittsfläche | mm2 |
| Bn | Berechnungsbeiwert für ovalförmige Querschnitte | - |
| CK | Berechnungsbeiwert | - |
| C | Wirksamkeit einer Randverstärkung | - |
| α | Winkel zwischen Grundkörper- und Abzweigachse Fußzeiger | Grad |
| b | Biegung | u | Umfang |
| l | längs | m | mittel |
| r | radial | B | Betrieb |
| t | Verdrehung | 0 | Einbauzustand |
a 3.1.2 Geltungsbereich
Die nachstehende Dimensionierungsberechnung gilt für Armaturengehäuse unter innerem Überdruck.
a 3.1.3 Berechnung der Gehäusekörper bei vorwiegend ruhender Innendruckbeanspruchung
a 3.1.3.1 Allgemeines
(1) Die Gehäusekörper können als Grundkörper aus einer geometrisch bestimmbaren Struktur mit Ausschnitten oder Abzweigen und Abzweigdurchdringungen aufgefasst werden. Die Berechnung der Wanddicken umfasst daher einmal den außerhalb des vom Ausschnitt beeinflussten Bereiches liegenden Grundkörperteil und zum anderen den Ausschnittsbereich selbst. Als Grundkörper des Gehäusekörpers wird dabei der Teil angesehen, der den größeren Durchmesser aufweist, so dass gilt dHi> dAioder b2> dAi.
(2) Die Übergänge unterschiedlicher Wanddicken sollen sprung- und knickfrei verlaufen, um ein abgestimmtes Verformungsverhalten zu erzielen. In Abhängigkeit von dem gewählten Nachweisverfahren der Spannungs- und Ermüdungsanalyse sind zusätzliche Konstruktionsanforderungen zu erfüllen, z.B. hinsichtlich der Übergangsradien (siehe Abschnitt 8.3).
Die Angleichung der Gehäusegrundkörperwanddicke sHnund der Abzweigwanddicke sAnan die anschließende Rohrwanddicke sRnsoll mindestens auf einer Länge von 2 ⋅ sHnoder 2 ⋅ sAnerfolgen. Für die Ausführungen des Übergangsbereiches sind zusätzlich die Festlegungen gemäß Abschnitt 5.1.2 (2) zu berücksichtigen.
(3) Für die Gesamtwanddicke mit Zuschlägen gilt:
| sHn> sH0+ c1 + c2 | (a 3.1 -1) |
| und | |
| sAn> sA0+ c1 + c2 | (a 3.1 -2) |
wobei sHnund sH0für den Grundkörper und sAnund sA0für anschließende Abzweige gelten.
(4) Für die Nachrechnung ausgeführter Bauteile ist zu setzen
| sH0d< sHn- c1 - c2 | (a 3.1 -3) |
| und | |
| sA0< sAn- c1 - c2. | (a 3.1 -4) |
a 3.1.3.2 Berechnung der Grundkörper außerhalb der Ausschnitts- oder Abzweigbereiche und ohne Randeinflüsse
a 3.1.3.2.1 Allgemeines
Die geometrische Struktur der Grundkörper der Armaturengehäuse kann zylindrisch, kugelig, kegelförmig oder oval sein. Entsprechend lassen sich die Wanddicken im ungestörten Bereich der Körper ermitteln.
a 3.1.3.2.2 Ermittlung der erforderlichen Wanddicke s0von zylinderförmigen Grundkörpern
Die Ermittlung der erforderlichen Wanddicke s0von zylinderförmigen Grundkörpern ist gemäß Abschnitt a 2.2.2 durchzuführen.
a 3.1.3.2.3 Ermittlung der erforderlichen Wanddicke s0von kugelförmigen Grundkörpern
Die Ermittlung der erforderlichen Wanddicke s0von kugelförmigen Grundkörpern ist gemäß Abschnitt a 2.3.2 durchzuführen.
a 3.1.3.2.4 Ermittlung der erforderlichen Wanddicke s0von kegelförmigen Grundkörpern
Die Ermittlung der erforderlichen Wanddicke s0von kegelförmigen Grundkörpern ist gemäß Abschnitt a 2.4.2 durchzuführen.
a 3.1.3.2.5 Ermittlung der erforderlichen Wanddicke s0von ovalförmigen Grundkörpern
(1) Bei ovalförmigen Querschnitten (Bild a 3.1-1) sind die in den Wandungen auftretenden zusätzlichen Biegebeanspruchungen zu berücksichtigen.
(2) Die theoretische Mindestwanddicke für solche Körper unter Innendruckbeanspruchung errechnet sich aus:
| (a 3.1-5) |
(3) Die Berechnung muss bei ovalförmigen Querschnitten für die in Bild a 3.1-1 gekennzeichneten Stellen 1 und 2 durchgeführt werden, da hier die das Festigkeitsverhalten im Wesentlichen beeinflussenden Biegemomente Größtwerte aufweisen.
Bild a 3.1-1: Ovalförmiger Gehäusekörper
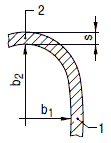
(4) Der von den Normalkräften abhängende Berechnungsfaktor B0 beträgt
für die Stelle 1: B0 = b1 / b2
für die Stelle 2: B0= 1
(5) Bnist dem Bild a 3.1-2 zu entnehmen.
Bild a 3.1-2: Berechnungsbeiwert Bnfür ovalförmige Querschnitte
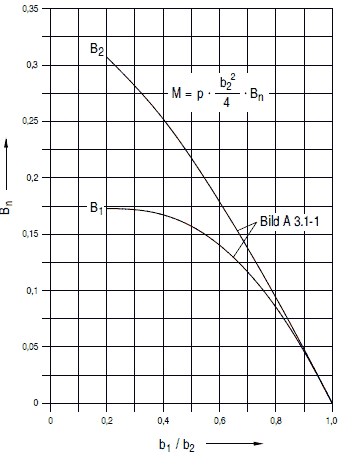
(6) Die von den Biegemomenten abhängenden Berechnungsbeiwerte Bn sind für ovalförmige Querschnitte für die Stellen 1 und 2 abhängig von b1 / b2in Bild a 3.1-2 dargestellt. Die Kurven entsprechen folgenden Gleichungen:
|
(a 3.1-6) |
|
(a 3.1-7) |
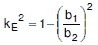 |
(a 3.1-8) |
Hinweis:
K´ und E´ sind die vollständigen elliptischen Integrale, deren Werte abhängig von dem Modul des Integrals kEaus Tabellenbüchern entnommen werden können, z.B. Hütte I, Theoretische Grundlagen, 28. Auflage, Verlag: W. Ernst u. Sohn, Berlin.
(7) Für die Berechnungsbeiwerte können für b1/ b2 größer als oder gleich 0,5 auch folgende Näherungsgleichungen benutzt werden:
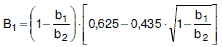 |
(a 3.1-9) |
| (a 3.1-10) |
(8) Die Berechnungsbeiwerte gelten auch für Querschnittsveränderungen in ovalen Grundkörpern, z.B. bei Schiebern nach Bild a 3.1-3. Ausführung a und Ausführung b, bei denen die Seitenlänge b1von der Scheitelzone des Einlaufstutzens (abgeflachtes Oval) über die Länge l bis auf den Wert b2 (Kreisform) zunimmt. Für die Ermittlung von Bnist dann der Wert b1im Querschnitt B-B bei l / 2 maßgebend. Dabei ergibt sich l aus
| (a 3.1-11) |
mit H als Konstruktionsmaß nach Bild a 3.1-3.
Für die vom Einlaufstutzen beeinflusste Länge l´ gilt:
| l´ = 1,25 ⋅ (d´m ⋅ sn)0,5 | (a 3.1-12) |
| mit d´m= b´1 + b2 / 2 | (a 3.1-13) |
wobei b21und b2am Querschnitt A-a im Abstand l´ vom Einlaufstutzen zu ermitteln sind. sn ist die bei l´ vorhandene Wanddicke. Hierbei sind b21und l2 im Allgemeinen iterativ zu ermitteln.
(9) Bei kurzen Gehäusekörpern (z.B. Bild a 3.1-3 Ausführung a oder Ausführung b) mit der ungestörten, der Berechnungsgeometrie entsprechenden Länge l kann die Stützwirkung der an den Enden anschließenden Bauelemente (z.B. Flansche, Böden, Deckel) mit in Rechnung gestellt werden. Damit ergibt sich mit Gleichung (a 3.1-5) die erforderliche Mindestwanddicke aus:
| s0 = s´0 ⋅ k | (a 3.1-14) |
Bild a 3.1-3: Beispiele für Querschnittsveränderungen in ovalen Grundkörpern
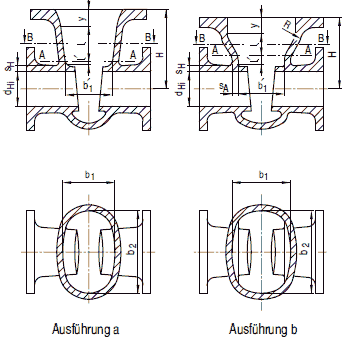
Bild a 3.1-4: Korrekturfaktor k für kurze Gehäusekörper

(10) Der Korrekturfaktor k ergibt sich in Anlehnung an das Abklingverhalten der Beanspruchungen in Zylinderschalen unter Berücksichtigung experimenteller Untersuchungsergebnisse an nichtkreisförmigen Gehäusen aus:
| (a 3.1-15) |
Die Funktion ist in Bild a 3.1-4 abhängig von l2 / dm ⋅ s´0 dargestellt.
(11) Für dm ist dm = (b1 + b2) / 2 zu setzen und s´0entspricht Gleichung (a 3.1-5). Bei Querschnittsveränderungen über der Länge l, z.B. nach Bild a 3.1-3 Ausführung a oder Ausführung b, sind die Maße b1und b2im Querschnitt B-B (bei l / 2) zu entnehmen. Örtliche Abweichungen von der Gehäuseform, seien sie konvexer oder konkaver Art, können in der Regel vernachlässigt werden.
(12) Dem Festigkeitskriterium ist genüge geleistet, wenn die erforderliche Wanddicke örtlich vorhanden ist, vorausgesetzt, dass Übergänge der Wanddicken sanft erfolgen.
a 3.1.3.3 Gehäusekörper mit Abzweig
(1) Die Festigkeitsberechnung des Gehäusekörpers mit Abzweig erfolgt aufgrund einer Gleichgewichtsbetrachtung zwischen den äußeren und inneren Kräften für die höchstbeanspruchten Zonen. Als solche werden die Übergangsstellen der zylindrischen, kugeligen oder nichtkreisförmigen Grundkörper zum Abzweig angesehen. Dem Grundkörper ist dabei der Durchmesser dHund die Wanddicke sHund dem Abzweig der Durchmesser dA und die Wanddicke sazugeordnet. Es muss gelten: dHi> dAi.
(2) Bei zylindrischen Grundkörpern, siehe Bild a 3.1-5, weist in der Regel die im Längsschnitt durch die Hauptachse gelegene Schnittstelle I mit der mittleren Hauptspannung σIdie größte Beanspruchung auf. Bei Verhältnissen von Stutzenöffnung zur Grundkörperöffnung größer als oder gleich 0,7 sind jedoch die im Querschnitt zur Hauptachse (Schnittstelle II) auftretenden Biegebeanspruchungen nicht mehr zu vernachlässigen, d. h. es ist dann auch diese Richtung zu berechnen.
Bild a 3.1-5: Berechnungsschnitte für Gehäusekörper mit Abzweig
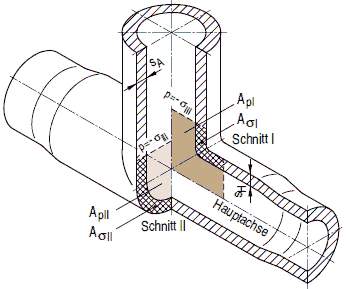
(3) Eine Nachrechnung für den Schnitt II kann entfallen, falls die Wanddickenunterschiede innerhalb der Abklinglänge dieses Schnittes und im Vergleich zu Schnitt I kleiner als oder gleich 10 % sind.
(4) Bei nichtkreisförmigen Gehäusekörpern mit Abzweigen und allgemein bei zusätzlichen Kraftwirkungen in Richtung der Hauptachse kann die größte Beanspruchung auch im Querschnitt mit der mittleren Hauptspannungsrichtung σII (Schnitt II) liegen.
(5) In diesen Fällen ist die Rechnung sowohl für den Schnitt I als auch für den Schnitt II durchzuführen.
(6) Das nachfolgende Berechnungsverfahren ist für Armaturengehäuse mit senkrechtem Abzweig (siehe Bilder a 3.1-6 bis a 3.1-12) sowie mit schrägem Abzweig, wenn der Winkel ± gleich oder größer als 45 Grad ist (siehe Bild a 3.1-14), zulässig. Dabei ist vorausgesetzt, dass sakleiner als oder gleich sHist. Ist bei Konstruktionen die Einhaltung dieser Bedingungen nicht möglich, kann nur die kleinere Wanddicke sHfür die Berechnung der mittragenden Länge und der tragenden Querschnittsfläche Aσverwendet werden.
Hinweis:
In den Bildern a 3.1-5 bis a 3.1-14 ist die dargestellte Wanddicke die Nennwanddicke abzüglich der Zuschläge c1 und c2.
(7) Für das Kräftegleichgewicht im Längsschnitt gemäß den Bildern a 3.1-6 bis a 3.1-12 gilt die Beziehung
| p ⋅ ApI= σI ⋅ AσI | (a 3.1-16) |
wobei p ⋅ Apldie äußere Gesamtkraft darstellt, die auf der drucktragenden Fläche ApI(gerastert) wirkt, während als innere Kraft σI⋅AσI die in der höchstbeanspruchten Zone der Wandung mit der Querschnittsfläche AσI (kreuzschraffiert) und im Querschnitt der mittleren HauptspannungσI wirksame Kraft anzusehen ist.
(8) Die nach der Tresca-Hypothese zu fordernde Festigkeitsbedingung lautet:
|
(a 3.1-17) |
(9) Bei nichtkreisförmigen Gehäusekörpern mit Abzweigen sind zur Berücksichtigung der Biegespannungen, die über die bei der Ermittlung der Wanddicken nach den Gleichungen (a 3.1-5) oder (a 3.1-14) bereits erfassten hinausgehen, folgende Festigkeitsbedingungen anzuwenden:
|
(a 3.1-18) |
(10) In den Gleichungen (a 3.1-17) und (a 3.1-18) wird die senkrecht zur Wandung wirkende Spannung σII, als kleinste Hauptspannung betrachtet, die auf der druckbeaufschlagten Seite σII, = - p und auf der drucklosen Seite σII, = 0, also im Mittel σIII = - p/2 ist.
Sinngemäß gilt für das Kräftegleichgewicht im Querschnitt II (siehe Bild a 3.1-6)
| p ⋅ ApII =`sII ⋅ AσII | (a 3.1-19) |
Die Festigkeitsbedingung lautet in diesem Falle
|
(a 3.1-20) |
und bei nichtkreisförmigen Gehäusekörpern
|
(a 3.1-21) |
(11) Bei zylindrischen Gehäusekörpern mit dAi = dHi > 0,7 und gleichzeitig auch sA0 / sH0< dA / dHist im Querschnitt II zusätzlich folgende Bedingung zu erfüllen:
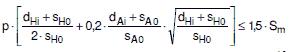 |
(a 3.1-22) |
(12) Für nichtkreisförmige Gehäusekörper lautet die Bedingung:
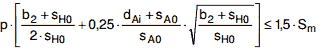 |
(a 3.1-23) |
Bild a 3.1-6: Gehäusekörper

(13) Für die in den Bildern a 3.1-7 bis a 3.1-14 dargestellten Fälle gilt allgemein die Festigkeitsbedingung:
| (a 3.1-24) |
Die drucktragenden Flächen Apund die tragenden Querschnittsflächen Aσwerden rechnerisch oder durch Planimetrieren (maßstäbliche Zeichnung) bestimmt.
Die mittragenden Längen der zu betrachtenden Querschnittsflächen Apund Aσmüssen wie folgt bestimmt werden (ausgenommen kugelförmige Gehäusekörper nach Bild a 3.1-11 und Abzweige mit schrägen Stutzen nach Bild a 3.1-14):
| eH= ((dHi+ sH0) ⋅ sH0)05 | (a 3.1-25) |
| ea= 1,25 ⋅ ((dAi+ sA0) ⋅ sA0)05 | (a 3.1-26) |
(14) Für die Darstellung in Bild a 3.1-6, Schnitt I gilt:
| eH = ((b1+ sH0) ⋅ sH0)0,5 | (a 3.1-27) |
| e A1= 1,25 ((dAi+ sA0) sA0)0,5 | (a 3.1-28) |
eA2gemäß Absatz (21).
Für Schnitt II gilt:
| e´H= ((b2 + sH0) ⋅ sH0)0,5 | (a 3.1-29) |
| eA3 = 1,25 ⋅ ((b2 + sA0) ⋅ sA0)0,5 | (a 3.1-30) |
(15) Bei Verhältnissen Stutzenöffnung zu Grundkörperöffnung größer als 0,8 entfällt in den Gleichungen (a 3.1-26), (a 3.1-28) und (a 3.1-30) der Faktor vor der Wurzel.
(16) Für Abzweige in kugelförmigen Grundkörpern mit Verhältnissen dAi1 / dHioder dAi2 / dHid 0,5 kann die mittragende Länge im Kugelbereich gemäß Bild a 3.1-11 Ausführung a angesetzt werden mit:
| eH= ((dHi+ sH0) ⋅ sH0)0,5 | (a 3.1-31) |
jedoch nicht größer, als es sich durch die Winkelhalbierende zwischen den Mittellinien beider Stutzen ergibt.
Für die mittragende Länge im Stutzen gilt
| eA = ((dAi+ sA0) ⋅ sA0)0,5 | (a 3.1-32) |
Bei Verhältnissen dAi1 / dHioder dAi2 / dHi> 0,5 wird wie in Bild a 3.1-11 Ausführung b vorgegangen, wobei eA1oder eA2 gemäß Gleichung (a 3.1-32) zu ermitteln sind.
Bild a 3.1-7: Gehäusekörper
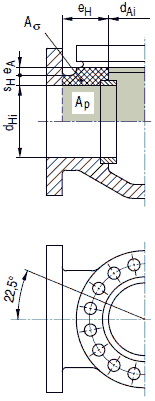
Bild a 3.1-8: Zylindrischer Gehäusekörper
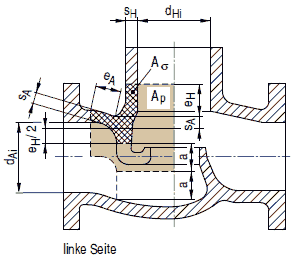
Bild a 3.1-9: Gehäusekörper in Eckform
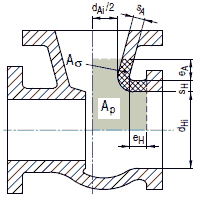
Bild a 3.1-10: Gehäusekörper
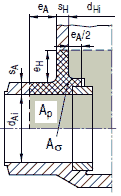
Bild a 3.1-11: Kugelförmige Gehäusekörper
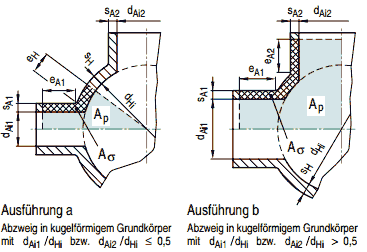
Bild a 3.1-12: Gehäusekörper
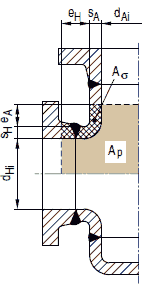
Bild a 3.1-13: Verschlussbeispiel
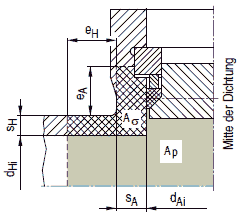
Bild a 3.1-14: Zylindrischer Gehäusekörper mit schrägem Abzweig

(17) Armaturengehäuse mit schrägem Stutzen (± e 45 °C) dÌrfen ebenfalls nach Gleichung (a 3.1-17) berechnet werden, wobei die Aufteilung der druckbelasteten Fläche (gerastert) und der drucktragenden Querschnittsfläche (kreuzschraffiert) nach Bild a 3.1-14 erfolgt.
Dabei sind die mittragenden Längen wie folgt definiert:
| eH= ((dHi+sH0) ⋅ sH0)0,5 | (a 3.1-33) |
| (a 3.1-34) |
Auch bei schrägen Abzweigen soll die Begrenzungsfläche der Druckfläche der Strömungsmittellinie folgen. Bei Verhältnissen Abzweigöffnung zu Grundkörperöffnung größer als 0,8 entfällt in Gleichung (a 3.1-34) der Faktor vor der Wurzel.
(18) Sollten Flansche oder Teile davon innerhalb der errechneten mittragenden Länge liegen, so sind diese, wie in den Bildern a 3.1-6, a 3.1-7, a 3.1-9, a 3.1-12 angegeben, als nicht mittragend anzusehen.
(19) Wenn mittragende Längen der Ausschnittsverstärkungen in den konischen Teil des Flanschansatzes hineinreichen, so darf nur der zylindrische Teil bei der Bestimmung der tragenden Fläche des Ausschnittes berücksichtigt werden.
(20) Sind im Bereich der tragenden Querschnittsfläche Aσoder im Einflussbereich von 22,51 zur Schnittfläche Bohrungen (Schraubenlöcher) vorhanden, so sind diese Querschnittsflächen von Aσabzuziehen.
(21) Nach innen überstehendes Material darf bis zu einer Höchstlänge von eH / 2 oder eA / 2 in die tragende Querschnittsfläche Aσ einbezogen werden.
(22) Bei Ausführungen nach Bild a 3.1-13, bei denen durch die Anordnung einer Dichtung sichergestellt ist, dass die drucktragende Fläche Apkleiner ist, als es der Abklinglänge eHoder eAentspricht, kann die Mitte der Dichtung als Begrenzung der Fläche Apzugrunde gelegt werden, während die Materialfläche Aσdurch die berechnete Länge eHoder eabegrenzt wird.
Bei Ausführungen mit druckdichtendem Deckelverschluss, bei denen der geteilte Segmentring innerhalb der Abklinglänge angeordnet ist, darf eHoder eafür die Bestimmung der tragenden Querschnittsfläche Aσbis höchstens Mitte Segmentring angesetzt werden, um die durch die Dichtung eingeleiteten Radialkräfte und die im Nutgrund auftretenden Biegebeanspruchungen zu begrenzen.
a 3.2 Gehäuseabschlüsse
a 3.2.1 Berechnungsgrößen und Einheiten zu Abschnitt a 3.2
| Formelzeichen | Berechnungsgröße | Einheit |
| a1, a2, aD, aF, aH, aS, aV | Hebelarme gemäß Bild a 3.2-1 | mm |
| b | tragende Breite des Flansches | mm |
| c1 | Zuschlag zur Wanddicke zur Berücksichtigung von Fertigungstoleranzen Zuschlag zur Wanddicke zur Berücksichtigung der Wanddickenminderung | mm |
| c2 | infolge chemischer oder mechanischer Abnutzung | mm |
| d1 | Durchmesser im Schnittpunkt Flanschblatt mit Kugelschale | mm |
| da | Außendurchmesser des Flansches | mm |
| d´a | Durchmesser der äußeren Kugelschale | mm |
| dD | mittlerer Durchmesser oder Durchmesser des Berührungskreises einer Dichtung | mm |
| di | Innendurchmesser des Flansches | mm |
| d´i | Durchmesser der inneren Kugelschale | mm |
| dL | Schraubenlochdurchmesser | mm |
| d´L | Berechnungsdurchmesser eines Schraubenlochs | mm |
| dp | Schwerpunktdurchmesser | mm |
| dt | Lochkreisdurchmesser | mm |
| hF | Höhe des Flanschblattes | mm |
| r´a | Radius der äußeren Kugelschale | mm |
| r´i | Radius der inneren Kugelschale | mm |
| s0 | Wanddicke der Kugelschale | mm |
| FD | Dichtungskraft | N |
| FDB | Betriebsdichtungskraft | N |
| FDBU / L | erforderliche Dichtungskraft für den Betriebszustand bei Krafthauptschlussverbindungen | N |
| FDV | Dichtungskraft im Einbauzustand | N |
| FF | Ringflächenkraft | N |
| FH | Horizontalkraft | N |
| FS | Schraubenkraft | N |
| FSBU / L | Mindestwert der Schraubenkraft für den Betriebszustand bei Krafthauptschlussverbindungen | N |
| FS0 | Schraubenkraft im Einbauzustand | N |
| FV | Vertikalkraft | N |
| Ma | Moment der äußeren Kräfte | N mm |
| MaB | Moment der äußeren Kräfte im Betriebszustand | N mm |
| Ma0 | Moment der äußeren Kräfte im Einbauzustand | N mm |
| Mb | Biegemoment | N mm |
| Mt | Torsionsmoment | N mm |
| Q | Querkraft | N |
| σBO | oberer Grenzwert der zulässigen Dichtungsflächenpressung im Betrieb | N / mm2 |
| σVO | oberer Grenzwert der Flächenpressung für die Vorverformung der Dichtung | N / mm2 |
| σVU | unterer Grenzwert der Flächenpressung für die Vorverformung der Dichtung | N / mm2 |
| µ | Reibbeiwert | - |
a 3.2.2 Tellerböden
a 3.2.2.1 Allgemeines
(1) Tellerböden bestehen aus einer flach- oder tiefgewölbten Kugelschale und einem anschließenden Flanschring. Die Festigkeitsberechnung umfasst daher die Berechnung des Flanschringes und die der Kugelschale.
(2) Entsprechend den geometrischen Verhältnissen wird unterschieden zwischen Ausführung I nach Bild a 3.2-1 als flachgewölbte Kugelschale (y > 0) und Ausführung II nach Bild a 3.2-2 als tiefgewölbte Kugelschale (y = 0).
a 3.2.2.2 Berechnung des Flanschringes
(1) Die Festigkeitsbedingungen für den Flanschring lauten:
| FH / 2 ⋅ π ⋅ b ⋅ hF< Sm | (a 3.2-1) |
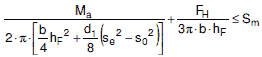 |
(a 3.2-2) |
Die Wanddicke s0 der Kugelschale ohne Zuschläge beträgt bei einem Durchmesserverhältnis d2a / d´i d 1,2
| s0 = ri ⋅ p / 2 ⋅ Sm - p | (a 3.2-3) |
| oder | |
| s0 = r´a ⋅ p / 2Sm | (a 3.2-4) |
mit d´a= 2 ⋅ r´a und d´i= 2 ⋅ r´i
Bei 1,2 d d2a / d2id 1,5 sind folgende Gleichungen für die Wanddicke s0 der Kugelschale anzuwenden:
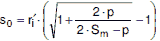 |
(a 3.2-5) |
 |
(a 3.2-6) |
Die Gleichungen (a 3.2-3) bis (a 3.2-6) liefern gleiche Ergebnisse, wenn r´i= r´a- s0gesetzt wird.
Bild a 3.2-1: Tellerboden mit flachgewölbter Kugelschale (Ausführung I, y > 0)
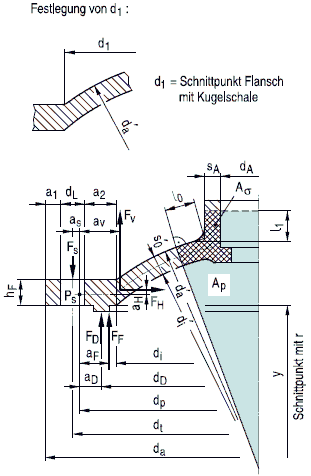
Bild a 3.2-2: Tellerboden mit tiefgewölbter Kugelschale (Ausführung II, y = 0)

(2) Das auf den Schwerpunkt PS des Flansches bezogene Moment Mader äußeren Kräfte beträgt für den Betriebszustand:
| (a 3.2-7) |
Die Dichtkraft FDwird bei Übertragung der Querkraft durch Reibschluss ermittelt aus:
| (a 3.2-8) |
Die Dichtkraft FD wird bei Übertragung der Querkraft durch Formschluss ermittelt aus:
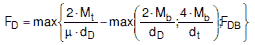 |
(a 3.2-9) |
Das Moment Ma beträgt für den Einbauzustand:
| Ma0= FS0(aS+ aD) | (a 3.2-10) |
Die im Uhrzeigersinn drehenden Momente sind in den Gleichungen (a 3.2-7) und (a 3.2-10) mit negativem Vorzeichen einzusetzen. Die Festigkeitsbedingung in Gleichung (a 3.2-2) ist mit beiden Momenten MaB und Ma0 zu rechnen, wobei für den Einbauzustand s0= 0 einzusetzen ist.
(3) Die Kräfte ergeben sich aus folgenden Gleichungen:
a) Schraubenkraft im Betriebszustand
|
(a 3.2-11) |
Für SDist mindestens der Wert 1,2 einzusetzen.
Beim Spannungsnachweis der Schrauben darf anstelle des Dichtungsdurchmessers dDder Lochkreisdurchmesser dteingesetzt werden.
FZwird bei Übertragung der Querkraft durch Reibschluss ermittelt aus:
| (a 3.2-12) |
FZwird bei Übertragung der Querkraft durch Formschluss ermittelt aus:
| (a 3.2-13) |
b) die Vertikalkomponente der Bodenkraft
| FV= p ⋅ π / 4 ⋅ di2 | (a 3.2-14) |
c) die Ringflächenkraft
| FF= p ⋅ π / 4 ⋅ (dD2 - di2) | (a 3.2-15) |
d) die Dichtungskraft im Betriebszustand
| FDBU / L= π ⋅ dD⋅ bD ⋅ σBU / L | (a 3.2-16) |
Die zulässige (maximal ertragbare) Standkraft der Dichtung im Betriebszustand beträgt
FDBO=p × dD ⋅ bD s σBO
mit
bD, σBU / Lund σBOgemäß Abschnitt a 2.10.
e) die Horizontalkomponente der Bodenkraft
| (a 3.2-17) |
mit
r = d´i / 2
Für den Einbauzustand gilt als Schraubenkraft FSOU
| FSOU= max. {FDVU / L⋅ SD; FSBU / L⋅ 1,1 } | (a 3.2-18) |
mit
FDVU= π⋅ dD⋅ bD⋅ σVU / L
SDmindestens 1,2
Im Einbauzustand darf die Dichtung höchstens mit
FDVO= π ⋅ dD⋅bD⋅ σVO
belastet werden.
σVU / Lund σVOgemäß Abschnitt a 2.10.
(4) Die Hebelarme der Kräfte in den Momentengleichungen (a 3.2-7) und (a 3.2-10) ergeben sich aus Tabelle a 3.2-1.
Tabelle a 3.2-1: Hebelarme für die Gleichungen (a 3.2-7) und (a 3.2-10)
| Hebelarm | Tellerboden | |
| Ausführung 1 | Ausführung 2 | |
| aS | 0,5 (dt- dp) | |
| aV | 0,5 (dp- d1) | |
| aD | 0,5 (dp- dD) | |
| aH | graphisch ermitteln | 0,5 ⋅ hF |
| aF | aD+ 0,5 (dD- di) | |
(5) Die tragende Breite des Flansches beträgt:
| b = 0,5 ⋅ (da- di- 2 ⋅ d´L) | (a 3.2-19) |
mit
d´L= v ⋅ dL
Für Innendurchmesser di größer als oder gleich 500 mm ist v = 0,5 und für dikleiner als 500 mm gilt v = 1 - 0,001 ⋅ di(diin mm).
(6) Der Schwerpunktdurchmesser dp ergibt sich aus:
| dp= da- 2 ⋅ Sa | (a 3.2-20) |
mit
|
(a 3.2-21) |
und
| a1= 0,5 ⋅ (da- dt- dL) | (a 3.2-22) |
| a2 = 0,5 ⋅ (dt- di- dL) | (a 3.2-23) |
a 3.2.2.3 Berechnung der ungestörten Kugelschale und des Übergangsbereiches Flansch / Kugelschale bei Innendruckbelastung
(1) Die Wanddicke s0der ungestörten Kugelschale ergibt sich aus den Gleichungen (a 3.2-3) bis (a 3.2-6).
(2) Für die Wanddicke seam Übergang vom Flansch zur Kugelschale gilt:
| se> s´e= s0⋅ β | (a 3.2-24) |
Bei dem Berechnungsbeiwert β wird berücksichtigt, dass bei dem großen Anteil Biegespannungen mit einer Erhöhung der Tragfähigkeit bei überelastischer Beanspruchung gerechnet werden kann. Geht man von dem die Tragfähigkeit kennzeichnenden Dehngrenzenverhältnis δ von gewÆlbten Böden aus, so kann bei Flanschen mit innen liegender Dichtung entsprechend Bild a 3.2-1 und Bild a 3.2-2 β = 3,5 gesetzt werden, was sich als N´herung aus Bild a 3.2-3 für β = α/ δ ergibt.
Bild a 3.2-3: Berechnungsbeiwert β für den Übergang Flansch / Kugelschale
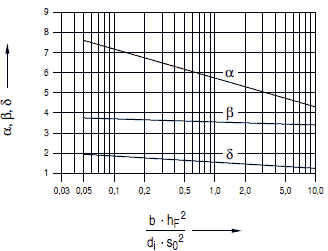
a 3.2.2.4 Ausschnittverstärkungen am Stopfbuchsraum von Armaturen bei Innendruckbelastung
Die Berechnung erfolgt nach dem Flächenausgleichsverfahren wie bei Böden mit Ausschnitten. Die Festigkeitsbedingung lautet:
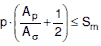 |
(a 3.2-25) |
Die mittragenden Längen sind:
| I0 = ((2 ⋅ r + s´0) ⋅ s´0)0,5 | (a 3.2-26) |
| I1 = ((da+ sA) ⋅ sA )0,5 | (a 3.2-27) |
mit s´0als ausgeführte Wanddicke im kugeligen Bereich abzüglich der Zuschläge c.
a 3.2.3 Gewölbte Böden
Die Berechnung von gewölbten Böden erfolgt nach Abschnitt a 2.5.
a 3.2.4 Ebene Platten
Abschlüsse in Form von ebenen Platten werden als äußere und innere Abschlüsse von Armaturengehäusen vielfach verwendet. Vornehmlich handelt es sich dabei um ebene Kreisplatten und Kreisringplatten wie sie in Abschnitt a 2.6.3.2 und a 2.6.3.3 aufgezeigt sind. Andere Plattenformen (z.B. rechteckig oder elliptisch) sind Sonderfälle, die der einschlägigen Literatur zu entnehmen sind. Bei Armaturen können überlagerte Lastfälle auftreten, die sich aus der Innendruckbelastung und zusätzlichen Kräften zusammensetzen. Die Lastfälle lassen sich dann in der angegebenen Weise auf Einzelbelastungen zurückführen und durch Summation der Momente erfassen. Hierbei ist jedoch zu berücksichtigen, dass die Maximalmomente der Einzelbelastungen nicht in jedem Fall das maximale Gesamtmoment ergeben. In diesem Fall muss die Lage und Größe des Maximums aus dem Verlauf der Belastungsfälle bestimmt werden.
Die Festigkeitsbedingung ist entweder in den Wanddickenformeln enthalten oder lautet explizit
|
(a 3.2-28) |
Die Dimensionierung von ebenen Platten erfolgt nach Abschnitt a 2.6.
a 3.3 Schrauben für Armaturen
Schrauben für Armaturen werden nach Abschnitt a 2.8 berechnet.
a 3.4 Selbstdichtende Verschlüsse
(1) Berechnungsgrößen und Einheiten zu Abschnitt a 3.4
| Formelzeichen | Berechnungsgröße | Einheit |
| a | Breite der Auflagerstelle | mm |
| b | Breite des Distanzringes | mm |
| bD | Breite der Dichtleiste | mm |
| da | Außendurchmesser des Gehäuses | mm |
| d0 | Innendurchmesser des Gehäuses | mm |
| d1 | Innendurchmesser der Gehäusenut | mm |
| d2 | Durchmesser des Verschlussdeckels | mm |
| h0 | Mindestkopfhöhe der Auflagerleiste | mm |
| hD | Mindesthöhe der Dichtleiste | mm |
| hv | Höhe des Verschlussdeckels | mm |
| h1 | Höhe des Einlegerings R | mm |
| s1 | Gehäusewanddicke in Höhe der Nut | mm |
| Fax | Axialkraft | N |
| FB | gleichmäßig über den Umfang verteilte Axialkraft | N |
| FZ | zusätzliche Axialkraft | N |
| MB | Biegemoment | N ⋅ mm |
(2) Die Festigkeitsberechnung hat die Untersuchung des schwächsten Querschnittes zum Ziel (Schnitt I-I oder II-II in Bild a 3.4-1). Gleichzeitig werden die wichtigsten Hauptabmessungen des Verschlusses nach elementaren Verfahren berechnet, z.B. der in die Nut eingelegte geteilte Ring R. Bei von Bild a 3.4-1 abweichenden geometrischen Verhältnissen dürfen die nachstehenden Formeln sinngemäß angewendet werden.
Bild a 3.4-1: Selbstdichtende Verschlüsse

(3) Die gleichmäßig über den Umfang verteilte Axialkraft errechnet sich aus:
| p ⋅ π / 4 ⋅ d02+ FZ | (a 3.4-1) |
FZist eine zusätzliche, gleichgerichtete Axialkraft (Gleichung a 3.4-3 bis a 3.4-8 über Verschlussstück eingeleitet; Gleichung a 3.4-9 und a 3.4-10 über Gehäuse eingeleitete Zusatzlasten, z.B. Axialkraft, Biegemoment). Im Falle eines Biegemomentes und einer Axialkraft wird FZ folgendermaßen bestimmt:
| FZ = Fax + 4 ⋅ MB / d1 + s1 | (a 3.4-2) |
(4) Die Mindestbreite der Druckflächen an der Auflagerstelle und am Distanzring ergeben sich unter Berücksichtigung der Reibungsverhältnisse und der Dichtungsanforderungen zu:
| a,b> FB / 1,5 ⋅p × d0⋅ Sm | (a 3.4-3) |
(5) Die Mindesthöhe des Einlegeringes R ergibt sich aus der Berechnung auf Abscheren und auf Biegung. Der dabei erhaltene größte Wert ist einzusetzen.
Hinsichtlich Abscheren gilt:
| h1> 2 ⋅ FB / π ⋅ d0 ⋅ Sm | (a 3.4-4) |
Hinsichtlich Biegung gilt:
| (a 3.4-5) |
(6) Die Mindestkopfhöhe der Auflagerleiste (Querschnitt II-II) ergibt sich aus der Berechnung auf Abscheren:
| h0> 2 ⋅ FB /p × d1 ⋅ Sm | (a 3.4-6) |
und gegen Biegung
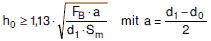 |
(a 3.4-7) |
(7) Für die Mindesthöhe der Dichtleiste gilt:
| (a 3.4-8) |
(8) Die Mindesthöhe des Verschlussdeckels hvkann durch Idealisierung als frei aufliegende Kreisplatte oder Kreisringplatte (Fall 1, Fall 7 oder Fall 8 aus Tabelle 5 von DIN EN 12516-2) ermittelt werden.
(9) Festigkeitsbedingung für Schnitt 1-1
| (a 3.4-9) |
und
| (a 3.4-10) |
a 3.5 Armaturenflansche
Armaturenflansche werden nach Abschnitt a 2.9 berechnet.
 |
weiter . |  |
(Stand: 18.09.2018)
Alle vollständigen Texte in der aktuellen Fassung im Jahresabonnement
Nutzungsgebühr: ab 105.- € netto
(derzeit ca. 7200 Titel s.Übersicht - keine Unterteilung in Fachbereiche)
Die Zugangskennung wird kurzfristig übermittelt
? Fragen ?
Abonnentenzugang/Volltextversion